Standard Candles in Astronomy

Contents

A standard candle is a class of astrophysical objects, such as supernovae or variable stars, which have known luminosity due to some characteristic quality possessed by the entire class of objects. Thus, if an extremely distant object can be identified as a standard candle then the absolute magnitude M (luminosity) of that object is known. Knowing the absolute magnitude, the distance D (in cm) can be calculated from the apparent magnitude m as shown in the formula below.

m = M - 97.5 + 5xlog(D) ---------- (1)

Figure 01 below shows the different kind of "standard Candles", including the Cepheid Variables (star), the planetary nebulae, and the Type Ia supernovae (together with other distance measuring tools).

Figure 01 Standard Candles

Parallax - The parallax of a star is the angle subtended at the star by the radius of the Earth's orbit (Figure 02). Distance to the star can be computed by the formula: d = 206265/p where the distance d is in unit of a.u., and the parallax p in second of arc. The usefulness of this method is limited by the resolution of the apparent positions to a distance of about 100 light years. A parsec is the distance corresponds to a parallax of 1 sec. of arc, i.e., 1 parsec = 206265 a.u. = 3.26 light years.

Figure 02 Parallax [view large image]

• Cepheid Variables - It was discovered in 1912 by the American astronomer Henrietta Leavitt that the period of the Cepheid

  		variables depends on the star's mean absolute magnitude; the more luminous the star, the longer the period (Figure 03a). From a graph or a formula it is possible to find the absolute magnitude of a Cepheid variable if its period is known. The distance to the star D can then be computed from Eq.(1). The Cepheid variables have proved extremely important for astronomy because they can be used to calculate the distance of objects far beyond the Milky Way. The same kind of relation is also applicable to the RR Lyrae stars. They are all about fifty times more luminous than the Sun, and they vary by about a magnitude in periods of between 0.2 and 1.2 days. Figure 03b shows the Cepheid Variable star RS Pup (behind the dark central stripe) surrounded by dusty reflection nebula. It is some 10 times more massive than the Sun and pulsates over a period of about 40 days.
  Figure 03a Period-Luminosity Relation	Figure 03b Cepheid Star RS Pup [view large image]

  
  
• TRGB (Tip of the Red Giant Branch) - This technique of measuring cosmic distance was discovered in the 21st century, here's some introductory comments :
  • When the main sequence star at the verge of using up the hydrogen fuel, its size expands in a phase called "Red Giant Branch" (RGB), which terminates at the point when helium burning commences. At this point, the size of the star reaches its maximum and ends with a flash (the helium flash).
  • For low mass ( < 2 M_Sun) main sequence star, the helium flash would occur at a particular absolute magnitude of M ~ - 4 corresponding to about 5x10³ L_Sun (see Figure 03c diagrams a, and b) and color index of (B - V) ~ +1.7, or (V - I) ~ +1.6 corresponding to a surface temperature of about 3000 K.

  Such peculiar point of the star can be relatively easy to pick out from the globular clusters in the halo of galaxy. For example, the TRGB can be located in the HR diagram of M5 (Figure 3c, diagram c), a globular cluster in the halo of the Milky Way. Converting the apparent visual magnitude mv to mI from the color indices, we obtain the distance D = 24 kly by applying Eq.(1). This value is very close to the 24.5 kly quoted by most literatures. For more distant galaxy, the tipping point can be identified by using the I-band, i.e., looking for (V - I) ~ +1.6 (the very red object). The TRGB methodology has been applied to many distant galaxies as shown in Figure 3c, diagram d. it complements the measurement by using the Cepheid Variables. The latest data produce a Hubble constant H0 ~ 70 (km/sec)/Mpc which sits right at the middle between the contentious measurements from nearby astronomical objects and

  Figure 03c TRGB

  the faraway CMB (see "Hubble Constant, 2018", "New Measure of Hubble Constant", and click the little icon  ).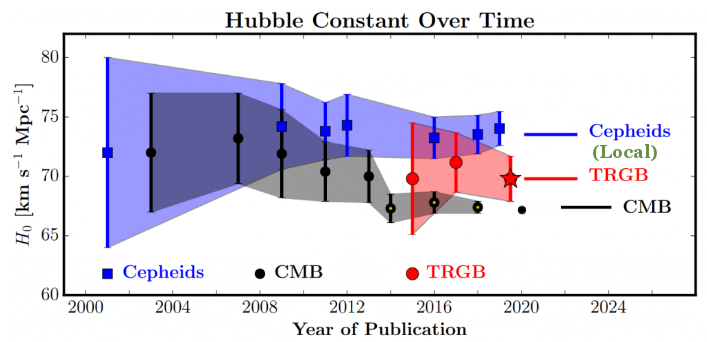

  
  
• Carbon Star - It is luminous red giant near the end of its life (Figure 03d), whose atmosphere contains more carbon than oxygen. These stars are redder in the near-infrared with definite absolute magnitude (Figure 03e) and thus can be used as standard candle. Its differences with TRGB are summarized by ChatGRP (in italic) :
  
  1. Composition:
  * TRGB stars are typically helium-burning stars, meaning they have exhausted their hydrogen fuel in the core and have transitioned to helium burning. They primarily consist of helium and hydrogen in their outer layers.
  * Carbon stars, on the other hand, are red giants with an overabundance of carbon in their atmospheres. This abundance of carbon is usually due to dredge-up processes, where carbon-rich material from the star's core is brought to the surface.
  
  2. Color and Spectral Characteristics:
  * TRGB stars are generally red giants with spectral types ranging from K to M. They exhibit reddish colors due to their cool temperatures and often display absorption features in their spectra associated with helium and molecular compounds.
  * Carbon stars are also red giants but are specifically characterized by strong absorption bands of carbon compounds, such as the Swan bands of C2. These stars often appear deep red or orange due to the prevalence of carbon compounds in their atmospheres.
  
  3. Evolutionary Stage:
  * TRGB stars represent a specific phase in the evolution of low to intermediate-mass stars, where helium burning is occurring in the core. They are typically found at the tip of the red giant branch in the Hertzsprung-Russell diagram.
  * Carbon stars can be found at various stages of the red giant branch, but they are specifically characterized by their high carbon abundance in their atmospheres. This carbon enrichment usually occurs later in the red giant phase due to internal nuclear processes.
  
  4. Mass and Luminosity:
  * TRGB stars can have a range of masses, typically between about 0.5 to 8 solar masses, and their luminosities can vary accordingly.
  * Carbon stars can also have a range of masses, but they are often more luminous than typical RGB stars due to their advanced evolutionary stage and enhanced stellar winds.
  

  		5. Occurrence: * TRGB stars are found in various stellar populations, including in globular clusters, dwarf galaxies, and the halo of our own Milky Way galaxy. * Carbon stars are less common than TRGB stars but are still found in various stellar environments, including in globular clusters, the halo of galaxies, and in certain regions of the Milky Way's disk.
  Figure 03d Carbon Stars	Figure 03e Carbon Star Luminosity [view large image]	In summary, while both TRGB stars and Carbon stars are red giants, they differ in their chemical composition, spectral characteristics, evolutionary stage, and occurrence in different stellar environments.




Planetary Nebula Luminosity Function - It is found that the statistical distribution of planetary nebula brightness in a galaxy obeys the so called planetary nebula luminosity function (PNLF) below: N(M) ~ e0.307M{1 - e3(M" - M)} ---------- (2) where N is the number of planetary nebula with absolute magnitude M, and M" represents the cutoff magnitude (there are no PN brighter than this), which is about -4.48. Thus, if we have a sample of PN from a given galaxy satisfying the PNLF as shown in Eq.(2), then we can obtain

Figure 04 PNLF [view large image]

the apparent magnitude m" corresponding to the cutoff magnitude M", and the distance D can be computed from Eq.(1). Figure 04 shows the theoretical and observed PNLF for M31.



• Tully-Fisher Relation - In stable orbit, the centripetal force of an object (be it a star or gaseous medium in the spiral arm) moves around a galaxy with mass M and rotational velocity V is balanced by the gravitational force such that:
  
  mV² / R = GmM / R² --------- (3)
  
  where m is the mass of the object. Assuming all galaxies have the same mass luminosity ratio (M/L constant) and the same surface brightness, i.e., I = constant = L /(4R²), then it follows from Eq.(3) that the luminosity L V⁴. Then the absolute

  magnitude M can be expressed in term of V, which can be measured from the line width of the 21-centimeter line emitted by the hydrogen cloud. This is known as the Tully-Fisher relation as shown in Eq.(4): M = 4.8 - 2.5xlog(L/Lsun) ~ 10xlog(V) ---------- (4) The distance D can be calculated by Eq.(1) once the apparent magnitude m of the galaxy is known. Figure 05 is an example of a Tully-Fisher relation between M and log(V). Each data point corresponds to a galaxy within the cluster of galaxies. The solid line represents the theoretical best fit.

  Figure 05 Tully-Fisher Relation [view large image]

• VLBI - Over the last decade, astronomers have been developing new techniques that will allow them to skip the distance ladder altogether - one of them is called Very Long Baseline Interferometry. Using the Very Long Baseline Array (VLBA) - a set of ten radio telescopes situated around the world from Hawaii to the Virgin Islands - astronomers can make direct distance measurement to spiral galaxies such as M106 (Figure 06). With the radio telescopes acting as one giant dish thousands of miles wide, they were able to tightly focus on the galaxy¹s core and measure the velocity of water masers - compact molecular clouds that emit an intense

  radio signal - swirling in a disk of gas at the galaxy¹s center. Combining the maser's intrinsic speed (inferred from Doppler shift of the maser emission) with the apparent angular motion as seen from Earth yields the distance D via the formula: D = V / (d/dt) ---------- (5) where V is the intrinsic velocity of the H2O molecular cloud measured from Doppler shift of the maser emission, and d/dt is the proper motion of the molecular cloud

  Figure 06 M106 [view large image]

  observed directly by the VLBI. Sometimes the proper motion of the jet is measured (instead of the molecular cloud) such as in the case of 3C273.

• TypeIa Supernovae - Type Ia supernova is the explosion of a white dwarf star in a binary star system. Material from a companion red giant star is dumped on the white dwarf until the smaller star reaches a precise mass limit. At that point the white dwarf can no longer support its own weight, and burns its nuclear fuel so suddenly that it explodes. These explosions always release roughly the

  		same amount of energy, and studies of relatively nearby type Ia supernovae have shown that they reach almost the same peak brightness in every case. Therefore it can be used as "standard candles" to determine their true distance. Figure 07 is a Type Ia supernova observed in 1994. It is the bright spot on the lower left at the fringe of the galaxy. Figure 08 shows such binary system before the explosion.
  Figure 07 Supernova Type Ia	Figure 08 Binary System [view large image]	The absolute magnitude for the Type Ia supernovae has been calibrated to be M = -19.33 0.25

• Sunyaev-Zeldovich Effect - The clusters of galaxies contains a hot, diffuse, gaseous intergalactic medium. The gas emits x-rays

through the bremsstrahlung process. The x-ray luminosity is proportional to 2S, where is the density of the gas, and S is the size of the cluster. While the Compton scattering process transfer energy between the gas and the photons of the cosmic microwave background, effectively casting a shadow on the CMBR. The cluster is dimmer when observed at low frequencies but brighter at high frequencies, relative to the CMBR as shown by the dotted line in Figure 09. The magnitude of this effect is proportional to S. The x-ray luminosity and the microwave variation are combined to obtain a direct measurement of the size S of the region containing the hot gas. While direct observation gives the angular size . Thus the distance D can be computed by the formula: D = S / ---------- (6)

Figure 09 SZ Effect [view large image]

• Gravitationally Lensed Quasars - When a galaxy is very close to the line-of-sight of a quasar, the light is deflected and many images of the quasar appear (Figure 10). As quasars are intrinsically variable objects, monitoring the luminosity variations of all images allows us to measure time delays between images, which is caused by splitting the light into slightly different paths around the lensing galaxy (see Figure 11). Computing the distance from the earth to the quasar requires the following information:

		The time delay -- which means the intensity of the background source must vary sharply, by large amounts. The angular separation of the images of the background source. the relative distances of lens and background source (we can use the redshift for this). the mass of the lens, and its distribution (a point mass, or uniform sphere, or a sphere with varying density, or an ellipsoid).
Figure 10 Lensed Quasar [view large image]	Figure 11 Time Delay [view large image]