CP Violation and Anti-matter

Contents

Matter Antimatter Asymmetry

Soviet physicist (and dissident) Andrei Sakharov pointed out three conditions necessary for the asymmetry to develop:


• The universe must be out of equilibrium - This is a natural consequence of the expansion of the universe. In this situation the particles and their corresponding antiparticles do not achieve thermal equilibrium due to rapid expansion decreasing the occurrence of pair-annihilation, and hence allowing a chance for the baryon-asymmetry process to take place.
• The conservation of baryon number must be violated - This , too, is inevitable during the epoch of the grand unification of the fundamental forces in the early universe when baryon number was not conserved.
• Laws of physics not the same for matter and antimatter - Otherwise any process that changes the amount of matter would be balanced by a similar effect for antimatter.

There are four different theories trying to explain the matter-antimatter asymmetry:


1. CP violation - The standard model of elementary particle suggests that when the universe was less than 10^-12 sec old, the condition was ripe for the production of more matter than antimatter with CP violation to provide the mechanism for different reaction rate (to produce matter and antimatter). The explanation sounds reasonable as described in the subsequent sections. However, theoretical calculation as well as experimental measurement shows an excess far too small to account for the observed degree of asymmetry.
2. Supersymmetry - Supersymmetry is one of the most promising extensions of the standard model of elementary particle. It demands many as-yet-unknown particles and perhaps new kind of interactions. It is suggested that new interaction outside the standard model might act differently on quarks and antiquarks, and produced the excess of quarks in our universe. Although there are inconclusive claims, so far there is no hard evidence for supersymmetry from experiments.
3. Leptogenesis - This explanation also requires new physics beyond the standard model. It assumes the existence of a new type of very heavy neutrino called singlet neutrino in the very early universe. According to the leptogenesis scenario, the singlet neutrinos would decay into either neutrinos or antineutrinos. Then the standard model predicts that certain reactions could occur in the very high-temperature conditions to convert antineutrinos into matter particles (and thus the lepton number is not conserved, e.g., from 0 to 2), eventually producing neutrons and protons leaving the universe devoid of antimatter (see neutrinoless double-beta decay). So far there is only one controversial claim in 2001 to have observed such reaction.
4. Electric dipole moment - The presence of an electric dipole moment (EDM) in elementary particles would allow matter and antimatter to decay at different rates leading to a possible matter-antimatter asymmetry. But all experiments including the one by ACME in 2014 have failed to detect such EDM. See "Axion" for an attempt to explain the absence or near zero of the EDM.

Kaon and Neutral B Meson Decays

		As shown in Figure 01, charge conjugation (C) reverses the sign of electric charge, changing a particle to its antiparticle. Parity (P) reverses the arrow on all vectors associated with the object. The laws of classical mechanics and electromagnetism are invariant under either of these operations, as is the strong interaction of the Standard Model. These symmetries however, are broken in the weak interaction. For many years, it appeared that the combined operation
Figure 01 CP Invariance [view large image]	Figure 02 Elementary Particles	(CP) were invariant even for weak interactions until it was shown to be otherwise in 1964.

decays into two charged pions (with CP=+1); the other is Klong with longer half-life, a CP state of -1 and decay into three neutral pions (with CP=-1). The 1964 experiment by Cronin and Fitch looked for the decay products of Klong. They observed a few decays of the Klong turning into pairs of oppositely charged pions: about 1 out of a total of 500 decays. This kind of decay arrives at a final CP state that is different from the initial CP state and proves that CP symmetry was not preserved exactly by the weak interaction.

Figure 03a Ko Meson Decays [view large image]

meson decay instead of -1/5000 calculated from the Standard Model. This result indicates that it requires new physics / new particle to explain the discrepancy (at 99% confidence level). The neutral B meson has the special property that it oscillates between the matter and anti-matter states as shown in Figure 03b (with the decay products of either a muon or anti-muon), where N--, N++ are the number of events corresponding to the matter or anti-matter mode respectively, and Aslb is the degree of CP violation. For an universe with perfect CP symmetry this number

Figure 03b Neutral B Meson Decays [view large image]

would be zero. Deviation from zero is first derived from the Standard Model (not quite enough with the fact that we are here), and now the new data requires a new theory to explain.

Standard Model and CP Violation

called "coupling constant" containing real and imaginary parts in general, i.e., it is a complex number. The set of coupling constants can be represented by the 3x3 CKM matrix (see Figure 04). In contrast with electric charge, which seems to come in a well-defined universal unit, each of these nine coupling constants is different. The triumph of the Standard Model is that it predicts a set of relationships between the nine elements of the CKM matrix and it predicts that they include properties that result in CP violation. The CP violation is related to the fact that the matrix elements include imaginary numbers. If we look at enough decays that involve the different matrix elements, we can see whether the relationships are true (there are only four independent parameters in the matrix).

Figure 04 CKM Matrix [view large image]

i

i

Figure 05 Unitarity Triangle

B Meson Decay

to pick up and study the decays of the many millions of B mesons created - hence these facilities are known as "B factories". Figure 06 shows the BaBar detector and the particle tracks from the B meson decay. The latest measurements yield a value of sine(2) = 0.78 0.08, which is exactly that needed to explain the magnitude of CP violation seen in the Cronin-Fitch experiment. However, these measurements also predict a value of one leftover proton to 1018 photons (resulting from the annihilation of particles and antiparticles). It is in disagreement with the observation of one in 109 by many order of magnitude.

Figure 06 B Meson Decay [view large image]

Leptogenesis (Revised 2021)

baryogenesis) suggests that an exceptionally heavy but unstable breed of Majorana neutrino existed in the very early universe. Their subsequent decay generated more anti-leptons than leptons. A mechanism called "Sphaleron" then converted 1/3 of the excess anti-leptons into baryons leading to the imbalance between matter and antimatter at the dawn of time. Theoretical analysis shows that leptogenesis works best when the neutrino masses are in the range 0.1 ev - 1 mev; the mass of the Majorana neutrino and the reheating temperature must be larger than 109 Gev.

Figure 07 Leptogenesis [view large image]

Such theory is the most favored mechanism to explain the matter anti-matter asymmetry because there is good circumstantial evidence for existence of various ingredients (except the requirement of heavy Majorana neutrino at reheating when particles were massless according to SM).

An experiment to look for neutrinoless double-beta decay (NDB, see Figure 08) is running since 1990 at the Gran Sasso laboratory near Rome. The claim for discovery is still in dispute. But the findings could confirm the neutrinos' changing behaviour (flip-floping between antineutrino and neutrino as shown in the lower diagram of Figure 08), and the existence of an extremely heavy form of neutrino at high temperatures (such as in the aftermath of the big bang). Note that the antineutrino disappears with the addition of one more proton (a baryon) in the NDB process.

Figure 08 NDB Decay [view large image]

		The NDB detectors are made from hundreds kilograms of appropriate isotope (such as the Germanium Detector Array in Figure 09) buried thousand meters underground to screen out cosmic radiation and covered with lead to block out unwanted radiation from other radiative elements. The signature for NDB (in lieu of the ordinary double-beta decay, see Figure 10) is revealed by definite energy of the two electrons (the end products) with the peak at about 2x103 kev. This is exactly
Figure 09 Ge Detector [view large image]	Figure 10 Double-beta Decay [view large image]	what the Gran Sasso lab has observed with 15 events in about 10 years from 1990. More careful work in 2006 eliminated 4 of these events. They also estimated the half-life of the NDB to be 2.2x1025 years and

Before going to the mathematical formalism, Figure 11 shows the time line leading to the domination of matter and beyond :



The Era of Inflation lasted from 10-35 to 10-33 sec. At the end of inflation, the inflaton field dumped its excessive energy to create particle/anti-particle pairs as it decayed to the true vacuum in a process called "reheating" (see also "Cosmic Inflation and Reheating"). It followecd a period with equal number of particles and anti-particles (all massless) until the "Spontaneous/Electroweak, Symmetry Breaking (SSB/ESB)" transition at 10-12 sec after BB. It it during this SSB/ESB process that particles became massive and leptogenesis transform the universe to matter only (see mathematical detail below).

Figure 11 Leptogenesis, Time Line [view large image]

CMB data reveal the extent of matter/anti-matter imbalance. It estimates 411 photons/cm3 as well as 4% of the total cosmic energy density (~ 10-29 gm/cm3) for baryons (mostly nucleons with mass ~ 1.6x10-24 gm), from which the ratio of matter/radiation = 6x10-10 is obtained.

Here's the mathematics :


• Leptogenesis is based on the following extension of the SM Lagrangian L₃ (see Figure 13). Beside the usual kinetic term, the interaction with the Higgs field is similar to the last term of L₃ with R (the right-handed lepton field) replaced by N (the right-handed heavy neutrino field) :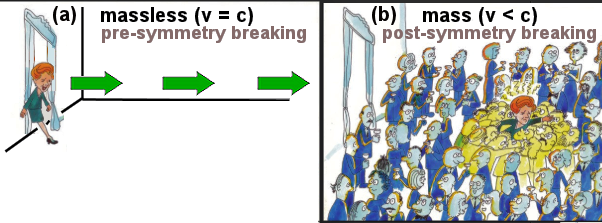
  

  Figure 12 Speed of Massless and Massive Particle [view large image]	(see Figure 12).

• In order to produce baryon asymmetry, it is necessary to satisfy the 3 conditions according to Andrei Sakharov :

  Baryon number violation - It could be fulfilled by the Sphaleron process which transform anti-leptons to baryons (Figure 07). It doesn't need energy to run in the symmetric phase before SSB/ESB. However, it requires lot of energy (~ 10 Tev) to operate afterward. Violation of C and CP invariance - It is expressed by : Thermal non-equilibrium - This condition is expressed by the wash-out indicator : Non-equilibrium is necessary to prevent excessive baryons to be wiped out by Sphaleron which can run both ways. This condition can be satified if the universe expands faster than the rate of reaction or decay leaving no chance for wash-out.

  Figure 13 Lepton Lagrangian [view large image]

  This condition determines the time when equilibrium is reached in relation to the processing of the following differential equations. The rate of cosmic expansion slows down over time, i.e., non-equilibrium previals mostly at earlier time.

• The asymmetry generation process is determined by the equations :
  
• Numerical Verification :
  • Development of matter/anti-matter asymmetry is assumed to occur at a short time interval about 10^-12 sec after BB around the processing of SSB/ESB (see Figure 14). The N neutrinos could be produced during reheating after inflation starting with an initial number density n₀. The solutions for n or n_B-L (in Eq.(2) or (4)) suggest that the N neutrino decay rate
    ~ 10¹² sec^-1 similar to many present-day meson decay.
  • The rate of cosmic expansion is expressed in term of the Hubble parameter H = (dR/dt)/R,

    where R is the scale factor for measuring the relative scale of the universe (R = 1, for the current epoch). The formula is : H = (8G/3)1/2 ~ 2.4x1012 sec-1 (for t ~ 10-12 sec), where ~ 1031 gm/cm3 (Figure 14) even through particles are restmass-less before SSB/ESB, this data is still meaningful since E = m0c2/[1-(v/c)2]1/2, and the gravitational constant G = 6.67x10-8 cm3/sec2-gm. Thus, the wash-out indicator k ~ 0.4 indicating that the system is in non-equilibrium state around the time frame of 10-12 sec.

    Figure 14 Cosmic History [view large image]

  • According to the Uncertainty Principle Et = 10^-27 erg-sec, if the N neutrino were created soon after the epoch of

    Inflation at 10-33 sec (see Figure 15), then its mass M (in term of energy E) should not be lower than /10-33, i.e., M 106 erg = 0.6x109 Gev. Similar argument can also be applied to its decay product of anti-neutrino produced up to 10-12 sec around the SSB/ESB transition giving MB-L 0.6x10-3 ev (most probably ~ 0.1 ev), which is compatible with experimental measurement. This is used as evidence to support the leptogensis theory.

    Figure 15 Early Universe [view large image]

  • This step involves some arithmetic, and finally deduced a value for the CP violation efficiency .
    • The observed matter/anti-matter asymmetry is given by = matter/radiation = 6x10^-10. The present-day radiation number density = 411 cm^-3 is interpreted as the result of matter/anti-matter annihilation leaving behind the baryonic number density ~ 2.5x10^-7 cm^-3.
    • The leptogensis theory above expresses = (1/3)(n_B-L/411) which yields n_B-L = n₀ = 7.5x10^-7 cm^-3.
    • In the very early time of 10^-33 sec soon after inflation, the linear scale is 10^-25 cm less with a corresponding reduction in volume of 10^-75 cm³. Thus, n₀ = 7.5x10⁶⁸ cm^-3, and the radiation number density is 411x10⁷⁵ cm^-3.
    • Taking the mass (energy) of the N neutrino M = 10⁹ Gev as mentioned above, the matter (energy) density
      ₀ = 10⁵⁴ gm/cm³.
    • As shown in Figure 14 the matter density ₀ = 10⁶⁵ gm/cm³ at that time, thus = 10^-11 is required to account for the observed asymmetry by leptogenesis. The "B Meson Decay" experiments produce ~ 10^-19 revealing that such CP violation mechanism is not sufficient.