 |
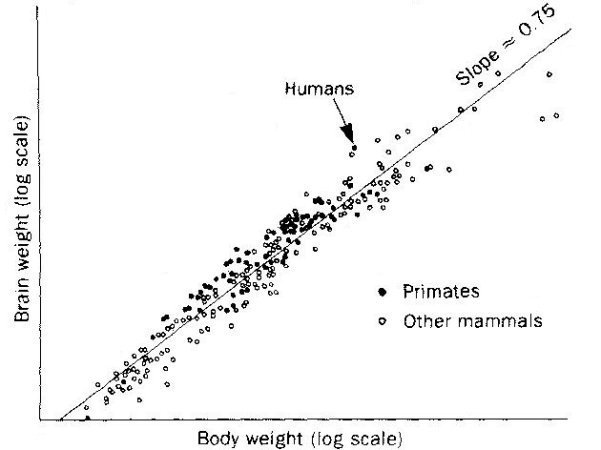 |
There is a more general 1/4 power-law applicable to many physicological variables y as shown in Figures 04, 05, and Table 01. The general form of the power-law is y  Mb, where b is a multiple of 1/4. It seems that all these physicological variables have something to do with the nutrient distribution networks and the dimensional dependence. For example, the life span is proportional to the linear dimension L, and the heart beat rate is related to the inverse L-1. The other variables simply follow the same 3/4 power-law or L3 as for the case of metabolic rate. Mb, where b is a multiple of 1/4. It seems that all these physicological variables have something to do with the nutrient distribution networks and the dimensional dependence. For example, the life span is proportional to the linear dimension L, and the heart beat rate is related to the inverse L-1. The other variables simply follow the same 3/4 power-law or L3 as for the case of metabolic rate.
|
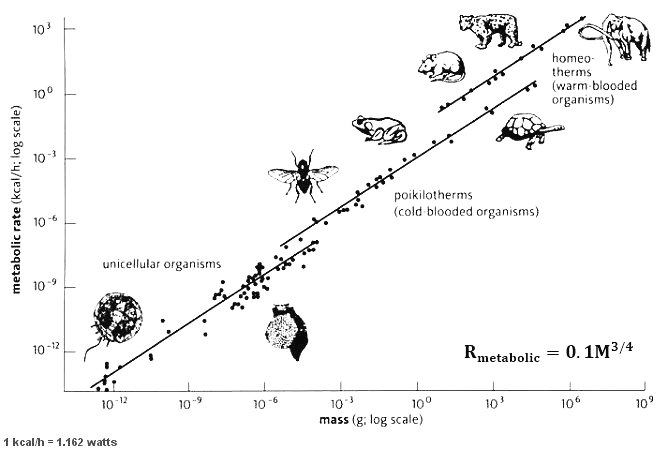

 M3/4. This is known as the Kleiber's Law. It holds good from the smallest bacterium to the largest animal (see Figure 01). The relation remains valid even down to the individual components of a single cell such as the mitochondrion, and the respiratory complexes (a subunit of the mitochondrion) as shown in Figure 02. It works for plants as well. This is one of the few all-encompassing principles in biology.
M3/4. This is known as the Kleiber's Law. It holds good from the smallest bacterium to the largest animal (see Figure 01). The relation remains valid even down to the individual components of a single cell such as the mitochondrion, and the respiratory complexes (a subunit of the mitochondrion) as shown in Figure 02. It works for plants as well. This is one of the few all-encompassing principles in biology.





 5x10-3 watts/gm. Whereas the R
5x10-3 watts/gm. Whereas the R 