Wave, Sound, and Music

Musical Instruments

		As shown in Figure 01a, musical instruments can be categorized into five types : strings, woodwinds, brass, percussion, and vocal (if the vocalists are considered as some sort of entertaining devices). Figure 01b displays the frequency range for different kinds of instruments (see an interactive version of the frequency chart). It is not an accident that the range follows closely with the human hearing perception from 20 to 20000 Hz. The followings concerns mostly with the excitation mechanism of the sound frequency and the amplification of the volume by various resonators. It is mainly the physics rather than the construction or properties of the instruments that will be considered here.
Figure 16a Types of Musical Instruments [view large image]	Figure 16b Frequency Range [view large image]

1. Strings - The formula governing the excitation of sound frequency is derived from the propagation of disturbances in a medium which can have a dimension of 1, 2 or 3 (see footnote on the mathematical derivation for the case of 1-D string) :

   and L is the length between the bridge (lower anchor) and the finger (upper anchor). Therefore, the frequency can be changed by placing the finger in different position and the device can be tuned by varying the tension. Excitation of the sound frequency is accomplished by moving the bow back and fore as shown in Figure 16c, which generates a triangular wave form. It can be resolved into a fundamental and many harmonics in

   Figure 16c String Instruments [view large image]

   terms of sine or cosine waves as expressed by the Fourier series f(x). Usually, the fundamental is the dominant component in the combination. Since different wave form

   decomposes to different harmonics thus, the placing of the bow has something to do with the sound spectrum called timbre.
   
   The vibration of string generates very low level of sound in the air. It is the resonator in the instrument that turns up the volume. The frequency at which the effect is most efficient, is called the resonant frequency. The resonance occurs inside the body is called "air resonance" while the material of the instrument also produces a different "wood resonance" frequency (see Figure 16c). It is via the

   bridge coupled to the soundboard, which transfers the string vibration into sound. The air resonant frequency can be approximated by the formula for Helmholtz resonance : , which was originally derived for air cavities such as the one shown in Figure 16d, where v = 34000 cm/sec is the sound velocity in the air. For a normal violin, V ~ 35.6x16.8x7 cm3, l ~ 0.2 cm, A ~ 3 cm2, the formula yields r ~ 320 Hz, which is very close to the measured value

   Figure 16d Helmholtz Resonance [view large image]

   of about 300 Hz. The wood resonant frequency is more difficult to estimated as it depends on the material and workmanship of the construction. Its measured value is about 450 Hz.

   
   Piano is sometimes referred to as keyboard instrument (a category including the pipe organ etc.) as it is played by pressing a key in the

   		keyboard (Figure 16e). The piano is actually a string instrument since the vibration is initiated by hitting a string with a hummer, which is hooked up to the key via a cumbersome mechanism called "action" (Figure 16f). Since the length of the string (piano wire) are much longer than those in violin, it has to be thin and at the same time tough to withstand high tension in order to
   Figure 16e Grand Piano [view large image]	Figure 16f Piano Action [view large image]	produce the range of frequency for smaller instruments such as the violin according to the formula.

   
   

   The principle of operation for the upright piano is similar. The design is to fold the strings, soundboard, and action 90o up toward the front (see Figure 16f). The pianos have the particular features that multiple hammers (up to three) are used simultaneously to produce sympathetic (harmonized) vibration, and they use dampers to control the vibration after the hammers hitting the strings in quick stroke. The right pedal raises all the dampers off the strings so that they keep vibrating after a key on the keyboard has been released. It adds much expressivity, allowing notes to resonate, and certain harmonies and notes to be connected together.

   Figure 16f Upright Piano [view large image]

   Similar to the smaller string instruments, the pianos also use bridge and soundboard to transfer vibration from string to air. Actually, there can be many air resonant frequencies when the

   enclosure is divided into pockets. However, the formula for Helmholtz Resonance is not applicable in this case.
   
   

   Then there is the inexpensive and simple erhu from ancient China. It uses only two strings with the bow attached together (making it hard to play for the beginner). The transmission of mechanical vibration to sound is mainly through the bridge and on to the python skin (in one end of the sound box), which creates sound at the same frequency of the string. The frequency range of the instrument is three and a half octaves, from D4 up to A7 (about 300 - 3.5k Hz).

   Figure 16g Erhu [view large image]

   The sound box resonates at about 1.7k Hz according to the calculation from the formula for Helmholtz Resonance (with V ~ 450 cm3, A ~ 45 cm2, and l ~ 1 cm).



2. Woodwinds - The woodwind instruments use either an open/open or open/closed pipe to create sound resonance inside as shown by the blue curve in Figure 16h, the corresponding pressure resonance is in red. The formula in term of the length of the pipe L can be expressed respectively as :

   n = nv/2L, n = 1, 2, 3 ... for open/open ends, and n = nv/4L, n = 1, 3, 5 ... for open one end. Since the standing wave can extend beyond an open end, L should be modified by adding a small amount of 0.3d, where d is the diameter of the pipe. In practice, the pipe is tapered toward the far end to implement the "equal-temperament" scale. The inexpensive recorder is a simple example to show how consonant notes are played by opening succesive holes on its length (see table in Figure 16h). The

   Figure 16h Woodwind Instrument [view large image]

   opening effectively creates a new pressure node with shorter "L" and higher frequency within the octave. Pressure inside the pipe is provided by blowing air from the mouth piece.



3. Brass - The resonant formula for the brass instruments is the same as for the woodwind. The differences are mainly on the ways the resonances are generated, and most of them are made with brass metal. Followings are some of the differences :
   • Energy Input - Brass instruments use the lips to create pressure variation within the pipe (Figure 16i,d), while the woodwinds blow air in to create density variation. However these two ways are equivalent, they are related by the formula for the ideal gas :

     	p = RsT, where p is the pressure, the density, T the temperature, and Rs = R/M the specific gas constant (R = 8.317x107 ergs/mole-K is the gas constant, M the molar mass in gm/mole, 1 mole = 6x1023 atoms or molecules).
     Figure 16i Brass Instrument [view large image]

   
   
   • Piston Valve - As shown in Figure 16i,2&3 the up and down movement of the valves closed and open the extra pipe connection thereby shortening or lengthening the pipe length, and thus the resonance frequency.
   • Tuning Slide - The other way to alter the pipe length is by moving the tuning slide back and fore to shorten or lengthen the pipe (Figure 16i,e&f).
   
   
4. Percussion - The percussion instruments can be considered as the sound board in the string instruments and piano. It is used to transfer mechanical vibration to sound. The material can be wood, metal, skin, etc. Such piece of plate (defined as length > width > thickness) produces non-harmonic sound (not in the ratio of 1:2:3... related to the fundamental frequency) when striked by a hammer. For example, the vibrational frequencies excited by hitting the drum are :
   
   

   = o (1, 1.59, 2.14, 12.30, 2.65, 2.92, 3.16, 3.50, 3.60, 3.65, 4.06, 4.15, ...), where the modes in bold are the ones where the drumhead is moving up and down at the middle; for the other modes, the center stays at rest while the vibration occurs on either side. The fundamental frequency is in the form : o = 0.7656(T/)1/2/D, where T is the membrane tension per unit length, the mass per unit area, D the diameter of membrane.

   Figure 16j Percussion Instrument [view large image]

   Many percussion instruments are made from thin metal bars, the resonant frequencies for which are non-harmonic as shown in Figure 16k, where the Young's modulus Y = stress/strain in unit of force per unit area. In the glockenspiel only the fundamental is audible, thus the bars can be adjusted to produce the consonant notes and appear as a musical instrument. The xylophone is similar but with variable thickness and tubes underneath to enhance the loudness. Chimes are also based on long bars. They choose the frequencies with n = 5, 6, 7 which form a ratio of 2:3:4 (in frequencies). The ear ignores the low tones and fills in the missing fundamental to hear a tone with harmonics.

   Figure 16k Metal Bar Instrument [view large image]



5. Vocal - Human voices are generated in the larynx, commonly called the voicebox (Figure 16l). It is situated inside the bump on the throat

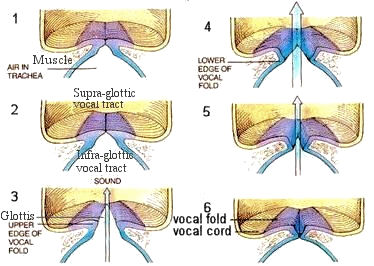   		called the "Adam's apple". The larynx is a multi-function organ used for swallowing, breathing, or talking. The larynx contains a membrane composed with the "vocal cords" (a misnomer) and the "vocal folds". When we breathe, the vocal folds relax and air moves through the space between them without making a sound. When we talk, the vocal folds tighten up and move closer together. Air from the lungs is forced between them and makes
   Figure 16l Voicebox [view large image]	Figure 16m Voice Production [view large image]	them vibrate, producing the sound of our voice. A loud sound will be created with a lot of air over the vocal

   membrane; while the pitch is controlled by the tension placed on the membrane. At the time of puberty, the growth of the larynx and the vocal folds is much more rapid and accentuated in the male than in the female, causing the male to have a more prominent Adam's apple and a deeper voice. Thus men will generally sing in the "tenor" range, or if their larynx gets a bit larger, the "bass" range; while women usually sing in the "soprano" range. The vocal membrane produces a basic vibration with little variation in tone color (timbre). It is up to the mouths and sinuses, among other organs, to shape the sound into a speech or melody. Figure 16n shows a typical bass voice by Louis Armstrong singing Blue Berry Hill together with many kinds of musical instruments.

   Figure 16n Louis Armstrong - Blue Berry Hill

   
   
   There are three steps in the production of voice:
   
   
   1. Production of airflow -- The default position of the vocal folds is open with no sound. It is closed immediately prior to voice production as shown in step 1 of Figure 16m. In step 2, air pressure develops below the vocal folds as the result of air from exhalation by the lungs. The power source for the voice is the infra-glottic vocal tract - the lungs, rib cage, abdominal, back and chest muscles that generate and direct a controlled airstream between the vocal folds.
   2. Sound Production -- Steps 3, 4, 5, and 6 (in Figure 16m) depict the rapid opening and closing of the vocal folds, which occur in a vibratory pattern and are responsible for sound production. After voice is produced, it is resonated throughout the supra-glottic vocal tract, which includes the pharynx, the tongue, the palate, the oral cavity and the nose. That added resonance produces much of the perceived character and timbre, or vocal quality, of all sounds in speech and song.
   3. Articulation of Voice -- Articulation refers to the speech sounds that are produced to form the words of language. The articulating tool comprises the lips, tongue, teeth, jaw, and palate. Speech is articulated by interrupting or shaping both the vocalized and unvocalized airstream through movement of these body parts. The teeth are used to produce some specific speech sounds.

Figure 16o Propagation of Disturbance in a String [view large image]

Go to Next Section
 or to Top of Page to Select
 or to Main Menu