Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ

Molecules

Contents

Quantum Theory, Blackbody Radiation (Revised in 2021)
Correspondence Principle
Uncertainty Principle
Complemetarity Principle
Exclusion Principle
Path Integral, Transition to Qunatum Theory
First Quantization, Schrodinger Equation (Revised in 2021)
Quantum Interpretations
Hydrogen Atom
Covalent Bond, Hydrogen Molecule
Ionic Bond, Atomic Shells
Hydrogen Bond, Molecular Orbital
van der Waals Force, Dipole-Dipole Interaction
Physical Chemistry
Adhesion and Cohesion
Inorganic Chemistry
Organic Chemistry
Soft Matter
Active Matter
Nano-technology
Perovskite
The Future of Chemistry

Quantum Theory, Blackbody Radiation (Revised in 2021)

Molecules are small objects not susceptible of direct observation even under the most powerful microscope. However, their properties can be deduced indirectly from experiments. These objects are different on the conceptual level as well. Classical physics can no longer
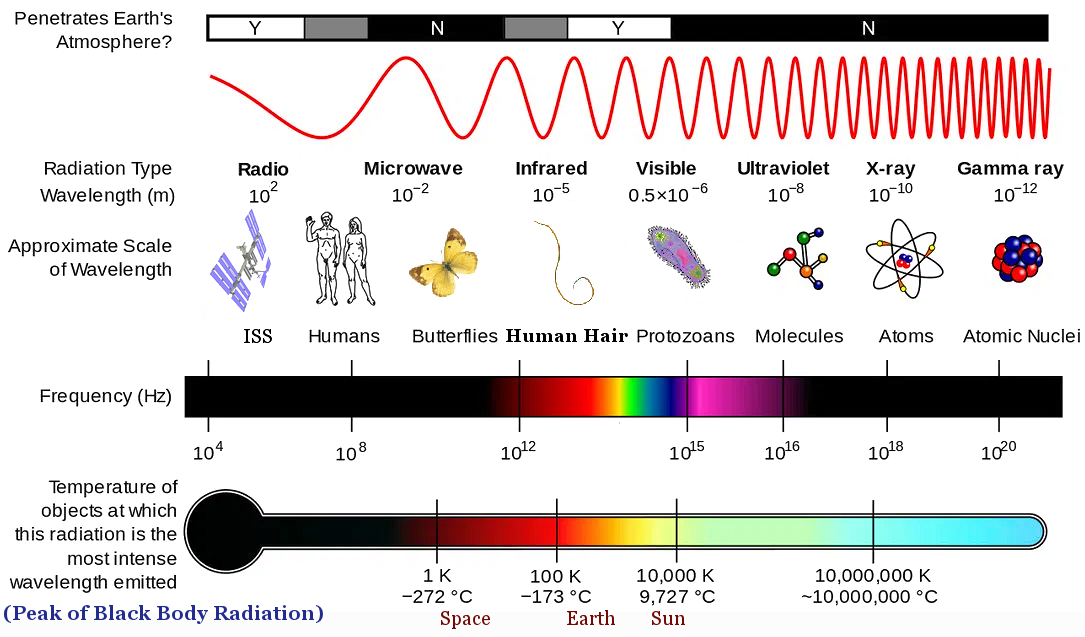
Blackbody Spectrum offer a consistent description. It is replaced by quantum theory, which describes the objects only in terms of probability, energy levels, and quantum numbers. A well-defined orbit similar to the path of a planet around the Sun becomes the probability of finding the object at a certain location in the microscopic world. Thus, all the illustrations related to these objects would be just a schematic diagram conveying some ideas, they should never be taken literally as the real thing (see objects smaller than 10-8 meter in Figure 12-01). Anyway, there is no such thing as probability, energy levels, and quantum numbers in nature; they are just abstractions invented by physicists to fit experimental data.

Figure 12-01 Blackbody Spectrum [view large image]
Historically, the quantum theory began with the attempt to account for the discrepancy between the theoretical and observational
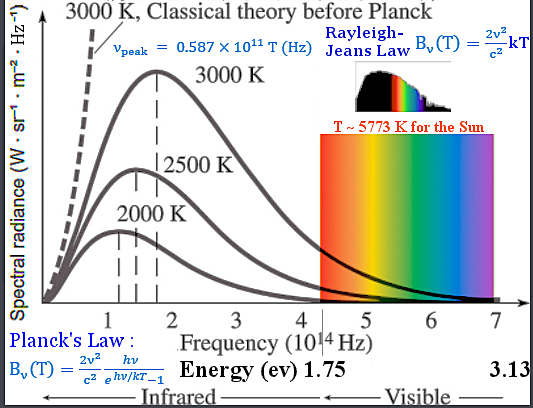Blackbody Radiation blackbody radiation. The classical theory of Rayleigh-Jeans failed to fit the observation of the radiation energy distribution from a blackbody at high frequency (Figure 12-02). In searching for a modification that would reduce the contribution of the high frequencies to the energy, Planck was led to make an assumption in 1899 : The energy of the radiation with frequency is restricted to integral multiples of a basic unit hv (a quantum), i.e., E = nh where h = 6.625x10-27 erg-sec is the Planck constant and n is an integer. With this assumption, Planck obtained an exact fit to the observed distribution of radiation energy. According to classical theory, electromagnetic radiation is a wave phenomenon. The Planck's assumption endows a particle aspect to the same entity. Such wave-particle duality requires radical changes in the fundamental concepts of the properties of matter and energy. An introduction on the subject of "wave" can be found in the special topic on Wave, Sound, and Music, also see "Energy of Single Particle".

Figure 12-02 Blackbody Radiation [view large image]

 The mathematical formula for black body radiation (Planck's Law) is shown in Figure 12-02 in the form of spectral radiance (per unit frequency) B(T). Note that the added exponential factor bends the Rayleigh-Jeans curve at high frequency and they agrees at low frequency.
See the mathematical details in footnote.

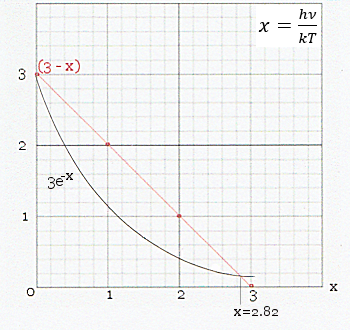
Peak Radiation Radiation/wavelength By defining x = h/kT, the Planck's Law becomes :
B(T) = [2(kT)3/(h2c3)][x3/(ex - 1)].
For a given temperature T, the maximum radiation would occur at peak determined by :
dB/dx = 0,
which yield (3 - x) = 3e-x.
As shown in Figure 12-03, the solution of this algebraic formula is x = 2.82, or peak = 0.587x1011 T (see Figure 12-02).

Figure 12-03 Peak Radiation [view large image]

Figure 12-04 Radiation/wavelength [view large image]
Based on thermodynamic argument, the "Wien's displacement law" was derivated in 1893. It states that the black-body radiation curve for different temperatures will peak at different wavelengths that are inversely proportional to the temperature, i.e., peak = (0.29/T) cm.

This formula can be derived from the Planck's Law in per unit wavelength (Figure 12-04) by the following transformation :
B = -(d/d)B = [2hc2/()5)][1/(ehc/kT) - 1].
By defining y = hc/kT, the Planck's Law becomes :
B(T) = [2(kT)5/(h4c3)][y5/(ey - 1)].
For a given temperature T, the maximum radiation would occur at peak determined by :
dB/dy = 0,
which yield (5 - y) = 5e-y.
Using similar graphic method as shown in Figure 12-03, the solution of this algebraic formula is y = 4.965, or peak = (0.29/T) cm.

Note that peak cannot be derived from peak as it would yield (peak)' = 1011 T, which is about twice of what it should be. This is because is inversely proportional to , i.e., = c/ and d = -(c/)(d/) = -(d/), i.e., it is not in a linear relationship.

When observation is made with no filter, energy would be captured from all the wavelengths or frequencies (and over the solid angle subtended by the object, see Figure 12-05,c), it is called the intrinsic intensity of the black body :
I(T) = B d = [2(kT)4/(h3c3)][x3/(ex - 1)]dx = [2(kT)4/(h3c3)](4/15) = T4,
Blackbody Luminosity where = (25k4)/(15h3c3) = 5.67x10-12 W/cm2-T4 is the Stefan–Boltzmann constant, and I(T) is known as the Stefan–Boltzmann Law ( Figure 12-05,a) formulated long time ago in 1879 by Austrian physicist Josef Stefan as a result of his experimental studies, the same law was derived again in 1884 by another Austrian physicist Ludwig Boltzmann from thermodynamic considerations.

Luminosity is the emitting power from the entire surface of the black body. In case of spherical black body such as the surface of star, L = 4R2I(T) = 4R2T4 (see Figure 12-05,b).
Such formula can be used to calculate un-measurable parameter from observable data.

Figure 12-05 Blackbody Luminosity [view large image]

 For example, the radius of the Sun can be determined from its luminosity and temperature in the HR diagram by R = (L/4T4)1/2 ~ 7x1010 cm (Figure 12-05,d).

A footnote for derivation of the Black Body formulas according to both classical and quantum perspectives.

The Rayleigh-Jeans formula is derived by considering the electromagnetic radiation to be a collection of standing waves of various wavelength inside the cavity (Figure 12-06). The number (of modes) density per unit wavelength is :
n() = 2/4, or per unit frequency n() = 22/c3,
Blackbody Radiation where the factor of 2 is inserted for the 2 different directions of polarization, the difference of 4 is related to the inclusion of the solid angle of the cavity.
By the "Equipartition Theorem", each mode of the standing wave has average energy of kT, thus we obtain the spectral radiance :
B(T) = (2c/4)kT, or B(T) = (22/c2)kT - the Rayleigh-Jeans Formula in spectral radiance.

Figure 12-06 Black Body Radiation, Classical and Quantum

In the derivation of the Planck's Law, the number density is replaced by the probability per unit volume per unit wave length (or per unit frequency) which happens to have the same form of n() or n(); but the mode of standing (electromagnetic) wave n = n in classical theory is replaced by the quantum of energy (the photon as a particle) En = nh, where h = 6.625x10-27 erg-sec is the Planck constant. The average energy is calculated by :



The diagram below summarizes the domains of activity in physics:

Phenomenological model is constructed to account for some data, while the theoretical framework encompasses a much wider scope including many phenomena. Usually the development of theories in physics follows the path from step 1 to 4 with constant feedbacks. Rarely does it proceed straight from Step 4 to 1. But such is the case from the brilliant insight of P. A. M. Dirac, who just wrote down the wave equation for the electron, the derived predictions were all verified to be correct. In another example, it took a genius like Einstein to start from a little bit of mathematics in the curvature of space (a small part in differential geometries, actually inspired by the pseudo-4D-flat-space in Special Relativity) and works its way backward to Step 1 with predictions way ahead of observations - many of those have been confirmed only recently.

Bohr Atom The formulation of Planck's Law is an example of phenomenological modeling, he just borrows the idea from the modes of standing wave and adds some modifications like the distribution of energy among the modes (the photons in the upgraded model). Another example is the Bohr atom (Figure 12-07), which transfers the standing wave pattern from straight line into a circle and assigns an energy to each level. Standing wave is a good analogy to quantum since the modes are in discrete amount of the fundamental mode. It is very useful in visualizing a stationary configuration.

Figure 12-07 Bohr Hydrogen Atom [view large image]

In mathematical terms, the relationship between standing wave and particle is established by the de-Broglie equation p = h/ and E = h, where p and E are the momentum and energy of the particle. Quantum theory is completely established by quantization of p and E, i.e., treating them as operators.

See Overview of the Quantum Theory (no mathematics), and "First Quantization".

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.