Molecules

First Quantization, Schrodinger Equation (Revised in 2021)

There were more experimental evidences (such as photoelectric effect, Compton scattering, etc) since the formulation of the Planck's Law in 1900. The new formula requires the quantization of energy in discrete amount. Theoretical development to reconcile the discrepancies with classical theory took about 25 years to something creditable. It happened that there are many routes to arrive at the solution, which basically is to treat the momentum p and energy E as operator (differentiation or otherwise), e.g., p i(d/dx) and E -i(d/dt). The followings are brief sketches to show the essence of the different methods.


1. Probability Wave (1900 - 1925) -
   • The nature of wave-particle duality was expressed mathematically by the de-Broglie relation (proposed in 1924) :
     p = h/,
     where p is the linear momentum of the particle and the wave-length of the wave.
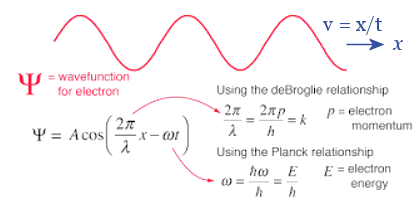
     The duality was explained by the difference in measuring apparatus. For example, the double slit experiment would show the interference of the electromagnetic wave, while photons in the form of particle are involved in photoelectric effect.
   • It turns out that it is actually the probability wave (NOT the EM wave) causing the duality. According to this interpretation, the particle has a certain probability of being this or that following the related wave pattern. In addition, the "wave" may not be the traveling variety, it could be standing wave, or any kind of form. From this point of view, it can be shown that the momentum p should be expressed as an operator in coordinate space :
     
     
   
   

   Note that the commnutation relation is satisfied in this differentiation form for p and x, i.e., xp - px = [x,p] = i, which is related to whether p and x can be measured simultaneously (= 0) or not ( 0), and the uncertainty principle px (see "Schwartz's Inequality"). This qunatization process also linearizes the classical equations with the dependent variable , which allows the superposition of different states creating all kinds of quantum weirdness such as being in 2 places at once (by applying quantum theory to macroscopic scale).

   Figure 12-05a Quantization [view large image]

   See Figure 12-05a,a for an even shorter introduction. See original derivation in Chapter 9, "Quantum Theory" by D. Bohm, 1951.

   Note Well : probability is a human concept to hide our ignorance about something or some process.
   
   
2. Matrix Mechanics (1925) - The formulation is based on the non-commutative relation between p (the linear momentum) and x (the spatial coordinate), i.e., xp - px = i. The scheme is implemented by matrices as shown in Figure 12-05a,b. The replacement of ordinary number by matrix can be interpreted as turning a definite entity into a blurry one, and that has exactly been shown by its relationship with the uncertainty principle px (see "Schwartz's Inequality").


3. Canonical Quantization (1926) - This method tries to derive a quantum version from the classical theory with minimal deviation.
   The Hamiltonian formulation of classical mechanics treats the dynamic of the system in terms of energy (aka Hamiltonian H, see Figure 12-05a,c), instead of force (as F = ma in Newtonian mechanics). It involves a mathematical term called Poisson Bracket (PB). For the case of coordinate x and momentum p, the PB {xp - px} = 1. Quantization just replaces the PB with the commutation rule [xp - px] = i from which we obtain p -i(d/dx), and all occurrences of p in the Hamiltonian H is substituted by such operator. See the wordy justification in 321 pages by P.A.M. Dirac in his 1926 thesis "The Principles of Quantum Mechanics".


4. Time Development Operator (2014) - A recent formulation does away all the baggages of the previous methodologies by starting with just a simple operator running in Hilbert space, i.e.,
   
   All quantum properties such as probability wave, commutation rules, uncertainty principle, and p = -i(d/dx) can be derived as shown in Figure 12-05a,d (with some hindsights ?). See "Short-cut to the Introduction of Quantum Theory" for more details, and the original book on "Quantum Mechanics" by L. Susskind, 2014.

		These examples do not exhibits qunatization of E. It occurs only when a potential (energy) V is added to the free particle equation and V has to be something like a well to confine the particle. Such general form is called Schrodinger Equation
Figure 12-05b Traveling Wave [view large image]	Figure 12-05c Standing Wave [view large image]	which has the time dependent part separated out similar to the standing wave. For a given interacting potential V the problem is to find the Energy E and the corresponding wave function .

This form of Schrodinger Equation can be used to find out the structure of the atom or molecule (in steady state and often with approximation). It was very important for finding out the intensity of spectral lines via the transition between energy levels. The basic concepts of superposition, perturbation, transition, and quantum measurement etc. can be explored in a system with an infinite square well potential, see "Mathematical Schrodinger's Cat (QM Basic)" for details. Another good example is the harmonic oscillator with V = kx2/2 (Figure 12-05d).

Figure 12-05d Energy Quantization

Go to Next Section
 or to Top of Page to Select
 or to Main Menu