Atoms

Specific Heats of Solids and Phonons

		atoms, the internal energy of a solid is assumed to reside in elastic standing waves. These waves, like electromagnetic waves in a cavity, have quantized energy contents. A quantum of vibrational energy in a solid is called a "phonon", and it travels with the speed of sound. The concept of phonones is quite general and has applications in connection with the thermal conductivity of some solids, the electrical conductivity in crystals, and in superconductivity. Calculation also reveals that contribution of electron
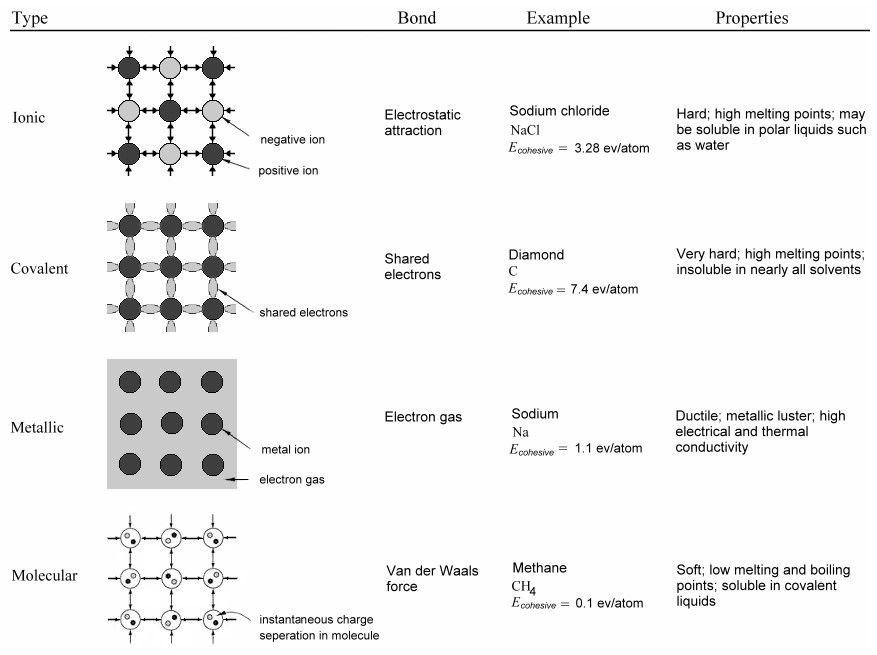
Figure 13-05a1 Crystal Types [view large image]	Figure 13-05a2 Specific Heats [view large image]	gas to the heat capacity is negligible except at very low temperature. The various models are shown graphically in Figure 13-05b1.

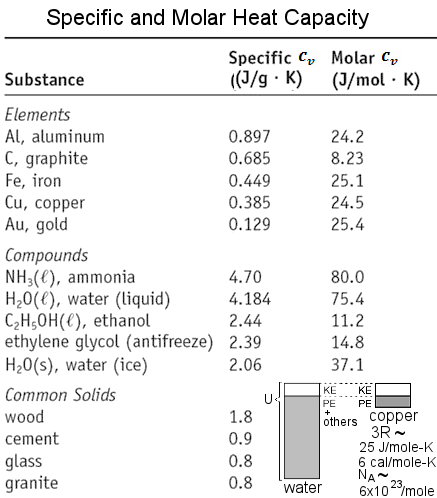		(~ 6x1023 particles in 1 atomic weight of the substance / mole = NA = Avogadro's number). Figure 13-05b2 lists the specific and molar heat for some selected substances. The conversion from J/g-K to J/mole-K is by multiplying the atomic weight. It leads to some curious situations that the relative amount is reversed after the conversion, (e.g.. graphite has higher value of specific heat than gold, but it is the opposed in molar heat because the latter has higher atomic weight). Since the hot or warm sensation is related to the temperature sensors on our skin, thus we would feel cooler for substance with high heat capacity from same amount of heat input (see insert in Figure 13-05a2).
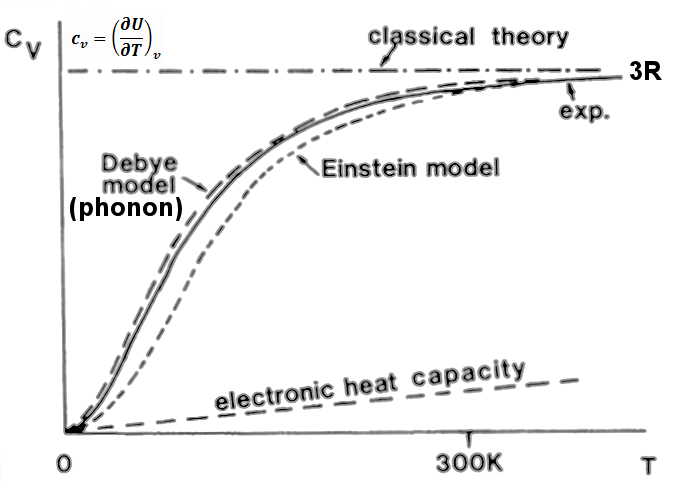
Figure 13-05b1 Specific Heat Theories [view large image]	Figure 13-05b2 List of Specific Heat	The 4 different models (as shown in Figure 13-05b1) that try to explain the behavior of heat capacity are derived in the followings :

(1) Maxwell-Boltzmann Distribution (Classical Theory) -

The law of thermodynamics dictates that infusion of heat dQ is to do work dW and/or to increase the internal energy dU, i.e.,

dQ = dU + dW .

For a piece of metal performing no work, with constant volume, and no change in the number of particles, each particle behaves like a simple harmonic oscillator (with no interaction), the heat would store into 3 degrees of freedom for the kinetic energy and another 3 degrees of freedom for the potential energy associated with the restoring force. This can be shown by considering each oscillator has energy E = mv²/2 + Kx²/2, from which calculation by Maxwell-Boltzmann statistics would yield an averaged energy of kT/2 for each degree of freedom (this is known as "theorem of equipartition of energy"). Accordingly, the internal energy U = N x 6(kT/2). For N = N_A the molar heat capacity at constant volume is :

These simple formulas have only limited applications to most metals and mono-atomic gases. Other substances have more complicated structure with internal energy stores in other forms (such as rotation and by large number of constituent atoms), which do not contribute to the raise of temperature, and thus would have large value of heat capacity. While some complex materials have relatively low heat capacity as the heat is stored independently by each atom, not by the bulk motion of the molecules (see Figure 13-05b2). This model cannot explain the behavior at low temperature. One of the attempts to resolve the problem is by using the quantized energy as shown presently.

(2) Quantum Theory - With the coming of quantum age, it was realized that the energy of the oscillators comes in quanta in the form of E_n = nh, where = (K/m)^1/2/ 2. Using the same Maxwell-Boltzmann energy distribution function, the averaged energy becomes :

See Figure 13-05b1 for comparison with experimental data.

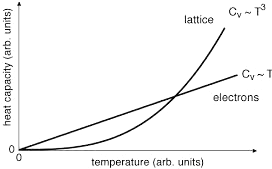(3) Electron Gas - The electron gas contribution to heat capacity can be estimated by considering that only those electrons near the Fermi energy EF can absorb the heat energy kT, i.e., N ~ NA(kT/EF). Therefore, the internal energy U ~ Nx(3/2)kT giving cv ~ (3/2)(kT/EF)R, which is very small comparing to the classical estimate of 3R and is not entirely satisfy with the T3 temperature dependence at low temperature (Figures 13-05b1 and 05b3)

Figure 13-05b3 Electron Gas Specific Heat

(4) Phonon - Since consideration of free oscillators fails to come up with an accurate description of the metallic heat capacity, the other extreme was used by treating the solid vibrating as whole. Standing waves within are generated and the wavelength or frequency is quantized similarly to the photon gas with averaged energy :

Figure 13-05b4 Phonon [view large image]	See Figure 13-05b4 to compare.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu