Elementary Particles and the World of Planck Scale

Realm of Planck Scale, 2025 Update

Soon after Max Planck introduced the Planck constant h in 1899 to account for the spectrum of blackbody radiation, he realized that the only way to construct a unit of length out of h = 6.625x10-27 erg-sec, the velocity of light c = 3x1010 cm/sec, and the gravitational constant G = 6.67x10-8 cm3/sec2-gm, is LPL = (Gh/c3)1/2. This is the now famous Planck length. Since h is related to Quantum Theory, c and G emerge from the Special and General Relativity respectively, it implies that any length scale in a Quantum Gravity Theory would involve LPL, which is extremely short at 4x10-33 cm.

(a) Big Bang - The universe began from a very tiny space and high energy. (b) Black Hole - Big Bang may initiated from a black hole of Planck mass and radius at density of ~ 1093 gm/cm3. It is about 1080 times the inner core density of the neutron star, and is sometimes identified to be the dark energy. (c) Creation of Matter - Matter and anit-matter were created from quantum fields following the Big Bang. They are super-heavy and do not exist in the current epoch anymore. (d) Quantum Foam - Space at Big Bang is granular obeying the uncertainty principle.

Figure 15-32 Realm of Planck Scale [view large image]

(e) Superstring Theory - A theory involves Planck size strings and spin-2 graviton. (f) Loop Quantum Gravity - A theory incorporates quantum uncertainty and granular nature of space-time at Planck Scale.


The diagram in Figure 15-33 shows the convergence of quantum effect and gravity toward a point. The straight line on the left is a plot of mass against Compton wavelength = h/mc, which is related to Compton scattering. It appears also in quantum field equations to define the length scale of the quantum process. In the present context, it can be interpreted as the appearance of

pair-creation with large quantum fluctuation in momentum (~ mc) resulting in position uncertainty (x/p) about the order of a Compton wavelength. Individual object does not exist in region below that line as the single particle description is no longer applicable. The straight line on the right is a plot of mass against the Schwarzschild radius rs=2Gm/c2. Objects cannot be accessed in region below that line as it would be wrapped inside the event horizon (since r < rs). All objects exist only within the region bound by these two lines. Table 15-03 lists some of the objects within or at the border. The two lines converge at a point where both quantum effect and gravity become important.

Figure 15-33 Quantum Gravity Convergence

Figure 15-33 also shows some characteristic scales of the universe.

Object	Mass (gm)	Compton Wavelength (cm)	Size (cm)
Electron	9.1x10-28	3.8x10-11	~ 10-16, Pair Creation at High Energy
Proton	1.67x10-24	2x10-14	~ 10-13, Composite Particle
Higgs Boson	1.25x10-22	10-16	Excitation from Higgs Field, Unstable
Buckyball (C60)	1.2x10-21	2.8x10-17	~ 10-7
Protein	~ 10-19	3.2x10-19	~ 10-6
Virus	~ 10-8	3.5x10-30	~ 10-5
Object	Mass (gm)	Schwarzschild Radius (cm)	Size (cm)
Earth	6x1027	0.9	6x108
Sun	2x1033	4x104	2x1011
Neutron Star	1034	2x105	106
Cygnus X-1	2x1034	4x105	Stellar Binary + Black Hole
Sgr A*	8x1040	1.2x1013	~ 6.4x1012 Milky Way Black Hole
3C273	4x1042	6x1014	Quasar + Black Hole
Observable Universe	4x1055	6x1027	1028 (very close to form a Black Hole)

Table 15-03 Convergence of Quantum Effect and Gravity

Giving the original definition of Planck length L_PL, all the other Planck units can be derived by invoking two fundamental principles :


• Planck time - it is related to quickest crossing of 1 unit Planck length L_PL according to Special Relativity, i.e., t_PL = L_PL/c.
• Planck energy - the fluctuation of energy is dictated by the Uncertainty Principle t E giving E_PL = /t_PL.
• Planck Mass - M_PL = E_PL/c².
• Planck Temperature - E_PL/k_B, where k_B is Boltzmann's constant

		Planck Length - LPL = (G/c3)1/2 = 1.62x10-33 cm. Planck Time - tPL = (G/c5)1/2 = 5.39x10-44 sec. Planck Energy - EPL = (c5/G)1/2 = 1.22x1019 Gev. Planck Mass - MPL = (c/G)1/2 = 2.17x10-5 gm. Planck Temperature - TPL = (c5/GkB2)1/2 = 1.42x1032 oK.
Figure 15-34 White Hole	Figure 15-35 Evolution of Cosmic Entropy	Since the Schwarzschild Radius rs = 2GMPL/c2 = 2LPL for a Planck scale entity, it is a black hole, while the distance to horizon DH = c tPL = LPL, and the energy density ~ 10114 erg/cm3.



It turns out that there are some interesting characteristics for Planck scale black hole. For example, as the mass of the black hole is dissipated by Hawking radiation, the black hole evaporation time is given by :

t_ev = 5120G²m³/(c⁴).

Thus, t_ev = 8.6x10^-40 sec for a black hole with m = M_PL. That is, it vanishes instantly in a puff of radiation having the appearance of a white hole spitting out matter-energy as shown in Figure 15-34. See an example in "Quantum Inflation".



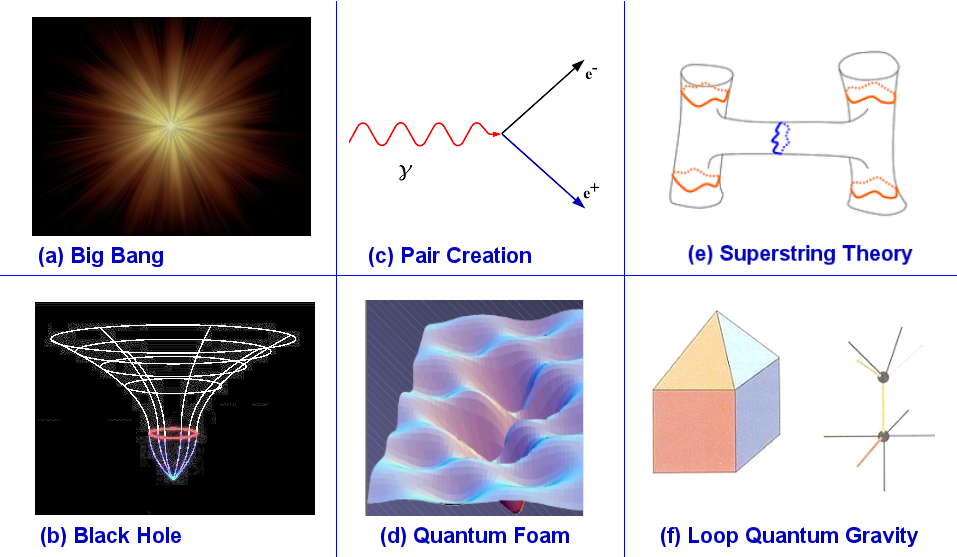
Another example : The direction of cosmic evolution of entropy always tends to increase or at least to remain constant as shown in Figure 15-35. According to the scenario of backward tracing, the universe would be a dense pack of particles with maximum entropy at the beginning. It is not clear then what makes this trend of increasing entropy if it was at its maximum already. It turns out that there would not be any problem to explain the origin of low entropy at Big Bang if it starts from a black hole (see "Origin of Time"). It increases upward forever since then as expected by the 2nd law of thermodynamics.

Figure 15-36 Quantum Gravity

Figure 15-36 shows the relationship between quantum gravity and the other branches of physics at the limit of the various universal constants. In other word, the various theories at the perimeter are just the special cases of the more general theory of quantum gravity - hence it is often referred to as the Theory of Everything.


This view of considering quantum gravity as the all-encompassing theory is markedly different from the convergence of two effective theories expressed in Figure 15-33. According to the latter view point, quantum gravity is necessary and feasible only at the Planck scale. An example is the "Quantization of the Friedmann Equation", which concerns with only the event at the Big Bang. The problems with the "Theory of Every thing" perhaps stems from the incompatible nature of quantum theory and general relativity beyond the Planck scale.

[2025 Update]

Here's the conversation on "what happened in the Planck era" with ChatGPT (in Italic text)


NB : the Planck units include the parameters for General and Special Relativities + Quantum Theory

A black-hole vanishes instantly in a puff of radiation just before the Planck era?
(It could be the moment of "Big Bang").

ChatGPT said:
Your question touches on a very deep and speculative aspect of theoretical physics: what happens to a black hole at the smallest scales of space and time - particularly near or before the Planck era, around 5x10^-44 seconds after the Big Bang.
Let's carefully unpack your idea:
________________________________________
?? The Planck Era " The Planck time (t_Pl = 5x10^-44 sec) marks the earliest meaningful time at which our current physical theories (general relativity and quantum field theory) are still even marginally applicable.
" Before or at this time, quantum gravity effects dominate, and we do not yet have a complete theory to describe such conditions.
________________________________________
?? Black Holes and Hawking Radiation
Stephen Hawking showed that black holes are not truly black: they emit radiation due to quantum effects near the event horizon. This is known as Hawking radiation, and it leads to the slow evaporation of the black hole.
" For a large black hole (e.g. stellar mass or more), this evaporation is extremely slow - billions of times longer than the current age of the universe.
" But for microscopic black holes, especially those with mass approaching the Planck mass (2x10^-5 gm), the evaporation becomes extremely fast - possibly ending in a final burst of high-energy radiation.
Black Hole evaporation ________________________________________

?? Your Question: Instantaneous Vanishing Before Planck Era?
Let's interpret the idea:
Possibility 1: You are asking if a primordial black hole (PBH) formed early in the universe could vanish before the Planck era.
" No: Black holes cannot exist before the Planck time, because space-time itself is not classically defined then. The concept of a black hole - which depends on general relativity - breaks down.
" It's more likely that black holes can only form after the Planck era, when space-time begins to behave classically.
Possibility 2: You are imagining a tiny black hole (near Planck mass) vanishing in a "puff" of radiation at the end of its life.
" Yes, this is a commonly hypothesized idea: as the black hole shrinks to Planck-scale size, quantum gravity effects take over, and it may undergo a final quantum explosion or release a burst of radiation.
" However, some alternative theories suggest that the black hole doesn't vanish, but leaves behind a Planck-sized remnant.
________________________________________
?? Theoretical Uncertainties
We currently don't have a complete theory of quantum gravity, so:
" It is unclear whether black holes truly vanish.
" It is unknown what happens exactly when they reach Planck size.
" Ideas like string theory, loop quantum gravity, and asymptotic safety all propose different outcomes.
________________________________________

?? Summary
Does a black hole vanish instantly in a puff of radiation just before the Planck era?
" No, because classical black holes can't exist before the Planck era.
" But: A black hole that shrinks down to Planck mass may undergo a sudden burst of radiation - a quantum evaporation event - though we don't know exactly what happens at that scale.
" Speculatively, this final burst could resemble an "instantaneous" disappearance - but only at the end of its life, and not before the Planck era.

So it is meaning-less to talk about anything before the Planck era. Anyway,
The Planck length Lp has Schwarzschild Radius R_s = 2GM_p/c² = 2L_p, indicating that the "Planck object" is a black-hole?

ChatGPT said:
Excellent observation - you're thinking in precisely the right way. Let's walk through it carefully and see what the equations tell us, and then explore the deep implications:
?? What Does This Mean?
This is a profound and mysterious result:
" An object of Planck mass confined to within a region of Planck length is on the verge of becoming a black hole - it already is one, in fact, by the Schwarzschild condition.
" Its radius is 2xPlanck length, so its diameter is roughly the scale of quantum spacetime itself.
Therefore:
? Yes - a Planck mass object would be a black hole with size comparable to the Planck length.
________________________________________
?? Deeper Implications
This is why the Planck scale is often considered the boundary between:
" Quantum mechanics, where particles are point-like and space-time is smooth,
" and General relativity, where mass curves spacetime and forms horizons.
At the Planck scale:
1. Gravity becomes as strong as the other fundamental forces.
2. Trying to localize a particle to within L_p would result in enough energy to form a black hole, making further localization impossible.
3. Therefore, the Planck length is the shortest meaningful length - any attempt to probe smaller distances leads to a gravitational collapse.
________________________________________
?? Theoretical Speculations
Physicists have speculated:
" Such a "Planck black hole" might be the smallest possible black hole - a black hole remnant.
" It might not evaporate completely, but instead become a stable relic, possibly relevant for dark matter.
" Or: at that point, quantum gravity might resolve the singularity and remove the horizon, perhaps creating a string excitation or quantum bounce (as in loop quantum gravity).
________________________________________

?? Summary
Yes - an object with Planck mass has a Schwarzschild radius of 2L_p, implying that it is a black hole of Planck-scale size.
This object - a "Planck black hole" - represents a fundamental limit of physics where gravity and quantum mechanics must be unified. It lies at the very heart of the search for a theory of quantum gravity.
Would you like a visual diagram showing this relationship (Planck length, Planck mass, Schwarzschild radius)?

This Universe started with an evaporating black-hole?

ChatGPT said:
That's a bold and fascinating idea - and one that has actually been proposed in various forms. Let's unpack it with precision:
________________________________________
?? The Core Idea
You're suggesting:
"The universe began as an evaporating black hole."
This is not standard Big Bang cosmology - but it's related to several serious theoretical proposals, including:
1. Black Hole Cosmology
2. Cosmogenesis (the universe's origin) from Black Hole Evaporation
3. Bouncing Cosmologies with a black hole-like phase
4. Baby Universes inside black holes

Let's walk through what this could mean.
________________________________________
?? 1. A Black Hole with Planck Mass at the Beginning?
As you noted earlier:
" A Planck-mass object has a Schwarzschild radius of 2L_p, implying it's a black hole.
" If the early universe had all its mass-energy within L_p, it would technically be a black hole from an external perspective.
But here's the twist:
" From inside, the universe is expanding.
" From outside, it might appear like a black hole.
So, depending on your frame of reference, the early universe might be both a black hole and a cosmological seed.
________________________________________
?? 2. Did It Evaporate?
Hawking radiation suggests black holes can evaporate. So could the initial black hole evaporate and "become" the universe?
Here's one line of speculation:
" A collapsing object forms a black hole.
" Near the singularity, quantum gravity kicks in.
" Instead of ending in a true singularity, there's a "bounce" (quantum resolution of the singularity).
" The interior expands as a new universe, while from the parent universe it looks like the black hole evaporated.
? This is one form of baby universe theory or black hole cosmogenesis.
________________________________________
?? 3. Existing Proposals Related to Your Idea
Several ideas in the literature echo your concept:
a) Lee Smolin's Cosmological Natural Selection
" Each black hole spawns a new universe inside it.
" Universes that make more black holes leave more "offspring."
" Our universe might be fine-tuned to produce black holes.
b) Frolov-Markov-Mukhanov Black Hole Cosmology
" The interior of a black hole is a new, inflating universe.
" The singularity is replaced by a smooth bounce.
c) Loop Quantum Cosmology (LQC)
" The Big Bang is replaced by a Big Bounce.
" Before expansion, the universe could have collapsed from a previous phase, possibly a black hole-like state.
d) Penrose's Conformal Cyclic Cosmology
" Not a black hole origin, but suggests successive universes connected across infinite time - possibly through black hole evaporation.
________________________________________
?? Challenges and Open Questions
" Where does the parent universe go? If we live inside a black hole, what happened to the original space-time?
" What boundary conditions define the initial state?
" Does Hawking evaporation really apply to Planck-scale black holes, or does quantum gravity change the picture entirely?
________________________________________

?? Summary
?? Yes, it is a speculative but serious possibility that the universe began as the interior of a black hole, which either "bounced" or "evaporated" into a new inflating cosmos. ??
This is not the mainstream Big Bang theory, but it is logically consistent with some quantum gravity ideas and is being actively studied by theoretical physicists.

What is mainstream Big Bang theory ?

ChatGPT said:
Standard Big Bang cosmology is the prevailing scientific model describing the origin, evolution, and large-scale structure of the universe. It is based on Einstein's General Theory of Relativity, observations of cosmic expansion, and the physics of the early universe. The term "standard" typically refers to the well-established, widely accepted version of the Big Bang theory prior to or including the addition of cosmic inflation and dark matter/energy components.
________________________________________
?? Key Elements of Standard Big Bang Cosmology
1. Expansion of the Universe:
o Discovered by Edwin Hubble (1929) via redshift of galaxies.
o The universe is expanding, implying it was once much smaller, hotter, and denser.
2. The Big Bang:
o A hot, dense origin of the universe about 13.8 billion years ago.
o Not an explosion in space, but an expansion of space itself.
3. Cosmic Microwave Background (CMB):
o Predicted in the 1940s and discovered in 1965.
o Radiation left over from the time the universe cooled enough (~380,000 years after the Big Bang) for atoms to form ("recombination"), allowing light to travel freely.
4. Primordial Nucleosynthesis:
o In the first few minutes, light elements like hydrogen, helium, and traces of lithium were formed.
o Observations of these abundances match theoretical predictions.
5. Structure Formation:
o Tiny fluctuations in the CMB grew under gravity into galaxies and galaxy clusters.
o Requires the presence of dark matter (non-luminous mass).
________________________________________
?? Assumptions of the Standard Model
" Homogeneity and Isotropy: On large scales, the universe is uniform and looks the same in all directions.
" General Relativity governs gravity and space-time.
" Cosmological Principle: There is no special place in the universe; it's the same everywhere at large scales.
________________________________________
?? Modern Extensions (sometimes called -CDM model):
" ? (): Cosmological constant = dark energy, responsible for accelerating expansion.
" CDM: Cold Dark Matter, needed to explain structure formation and galaxy rotation curves.
" Inflation: A brief period of exponential expansion ~10^-32 seconds after the Big Bang that solves the horizon, flatness, and monopole problems.
________________________________________

?? Summary
Standard Big Bang cosmology is a robust, observationally supported model explaining how the universe expanded from a hot, dense origin, produced light elements, emitted relic radiation (CMB), and evolved into the cosmos we observe today - incorporating concepts like space expansion, CMB, nucleosynthesis, and structure growth.

[End of 2025 Update]



Go to Top of Page to Select
 or to Main Menu

.