
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
A compressional wave in air can be set up by the back-and-forth motion of a speaker as shown in Figure 09. Here, the air molecules are alternately pressed together and pulled apart by the action of the speaker. The result is a propagating wave in which the pressure (and density) of the air varies with distance in a regular way - the pattern is, in fact, exactly the same as the displacement pattern of a transverse wave on a string (see Figure 01 and 02). Compressional waves in air are called sound waves, which are always longitudinal waves with the vibration parallel to the direction of propagation. Most of the previously mentioned concept about waves can be applied to the sound wave without modification except the formula for the wave velocity in Eq. (3) where the tension is replaced by the "bulk modulus" (change in pressure / change in volume) and the linear density is just the density of the air. It turns out that the velocity of sound at STP is about 330 m/s. |
Figure 09 Sound Wave |
 |
f = f0 x 2n, ---------- (8) where n = 0, 1, 2, 3, ... describes the octave relationship such as 20 (unison), 21 (one octave), 22 (two octaves), 23 (three octaves), ... Within the range of an octave, there is a series of frequencies called consonant intervals, which is known to produce the most pleasing sounds to the ear. They are usually combinations of notes related by ratios of small integers, such as the fifth (3/2) or third (5/4). Many musical instruments are tuned according to these intervals. Unfortunately, this kind of tuning depends on the scale - the tuning for C Major is not the same as for D Major. The "equal-temperament" scale solves the problem by dividing the octave into twelve equal intervals, each has a size of 21/12 x f, where f is the fundamental or harmonic frequency. It was developed for keyboard instruments, such as the piano, so that they could be played equally well (or equally bad) in any key. It is a compromised tuning scheme. |
Figure 10 Musical Scale |
| Note | Syl- lable |
Consonant Interval | Ratio | Decimal | E-T Interval (n)/(¢) | E-T Scale, 2n/12 | Difference/(in ¢) |
|---|---|---|---|---|---|---|---|
| C | Do / 1 | octave (fundamental) | 1/1 | 1.000000 | n = 0 / 000 | 1.000000 | 0.000000 / 00.0 |
| C# | minor second | 25/24 | 1.041667 | n = 1 / 100 | 1.059463 | -0.017796 / -29.3 | |
| D | Re / 2 | major second | 9/8 | 1.125000 | n = 2 / 200 | 1.122462 | +0.002538 / +3.91 |
| D# | minor third | 6/5 | 1.200000 | n = 3 / 300 | 1.189207 | +0.010793 / +15.6 | |
| E | Mi / 3 | major third | 5/4 | 1.250000 | n = 4 / 400 | 1.259921 | -0.009921 / -13.7 |
| F | Fa / 4 | fourth | 4/3 | 1.333333 | n = 5 / 500 | 1.334840 | -0.001507 / -1.96 |
| F# | diminished fifth | 45/32 | 1.406250 | n = 6 / 600 | 1.414214 | -0.007964 / -9.78 | |
| G | So / 5 | fifth | 3/2 | 1.500000 | n = 7 / 700 | 1.498307 | +0.001693 / +1.96 |
| G# | minor sixth | 8/5 | 1.600000 | n = 8 / 800 | 1.587401 | +0.012599 / +13.7 | |
| A | La / 6 | major sixth | 5/3 | 1.666666 | n = 9 / 900 | 1.681793 | -0.015127 / -15.6 |
| A# | minor seventh | 9/5 | 1.800000 | n = 10 / 1000 | 1.781797 | +0.018203 / +17.6 | |
| B | Ti / 7 | major seventh | 15/8 | 1.875000 | n = 11 / 1100 | 1.887749 | -0.012749 / -11.7 |
| C | Do / 1 | octave (1st harmonic) | 2/1 | 2.000000 | n = 12 / 1200 | 2.000000 | 0.000000 / 00.0 |
| Loudness | Intensity (watts/m2) | Intensity Level (dB) |
|---|---|---|
| Threshold of hearing | 10-12 | 0 |
| Rustle of leaves | 10-11 | 10 |
| Whisper | 10-10 | 20 |
| Watch ticking at 1 m | 10-9 | 30 |
| Radio (low) | 10-8 | 40 |
| Quiet conversation | 10-7 | 50 |
| Quiet motor at 1 m | 10-6 | 60 |
| Busy street traffic | 10-5 | 70 |
| Door slamming | 10-4 | 80 |
| Heavy truck, 50 ft | 10-3 | 90 |
| Power mower | 10-2 | 100 |
| Pneumatic drill | 10-1 | 110 |
| Near aeroplane engine | 1 | 120 |
| Physical damage | 10 | 130 |
 |
the sound as it gets louder. A piano tone constantly changes in timbre as it decays after it is sounded. Timbre is altered by the player for expressive reasons. Subjectively, strong upper harmonics are responsible for making an instrument's sound "bright" or "piercing". If the lower harmonics become dominant, then the sound would be "darker" or "duller". Figure 11b shows explicitly the generation of the fundamental and harmonic frequencies when a note is played on a piano key, e.g., the middle C (C4) key. Mathematically, such combination of frequencies is unavoidable because sound wave is governed by a linear differential equation such as Eq.(4a), which is similar to the Schrodinger equation in quantum mechanics, where the amplitude is related to the probability of finding the system in a particular quantum state (instead of the intensity of each frequency in the note).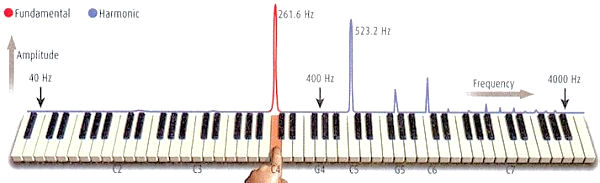
|
Figure 11a Timbre |
Figure 11b Fundamental and Harmonic |