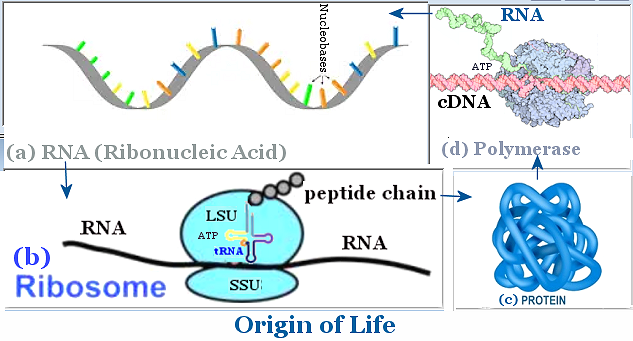
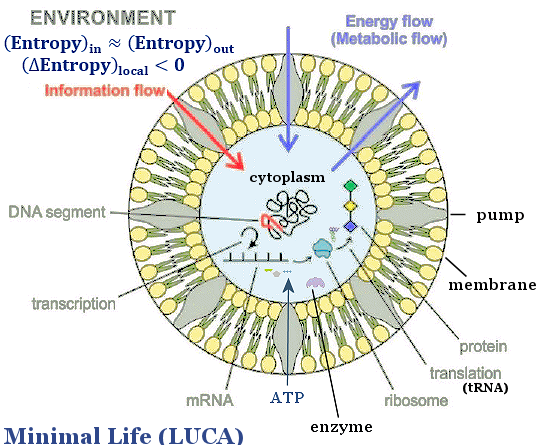
|
 |
In Local Equilibrium Thermodynamics, the whole system is not in equilibrium; but the intensive variables such as T, P, ... can be defined within a small volume, i.e., they are homogeneous (well-mixed) inside that volume (Figure 04,a). In addition, if the system can be described by mathematical formulas, then these intensive variables have to be differentiable, i.e., the functions should be smooth, continuous, and no break, angle, or cusp so that the derivative exists across the
|
Figure 04 Local Equilibrium Thermodynamics  |
|
whole system (Figure 04,b). Accordingly, the so-called Gibbs equation in the form of Eq.2 can be carried over with the difference " " replaced by the differential "d" (see Figure 04,b) : dU = TdS - PdV + " replaced by the differential "d" (see Figure 04,b) : dU = TdS - PdV +  dN ----- (3). dN ----- (3). |
 , temperature T, pressure P, chemical potential
, temperature T, pressure P, chemical potential  , ... In equilibrium thermodynamics, the intensive properties are homogeneous, isotopic, and unchange through out the system. Such requirements are identified as :
, ... In equilibrium thermodynamics, the intensive properties are homogeneous, isotopic, and unchange through out the system. Such requirements are identified as :

 U = T
U = T


 (II
(II I) ~
I) ~ 
 (
(
 0, there would be entropy dissipation even when
0, there would be entropy dissipation even when  0, (SII - SI) can be negative (driven by free energy infusion) as long as the inequality is satisfied. It means that orderly product can be created out of irreversible process at the expense of generating dissipative entropy
0, (SII - SI) can be negative (driven by free energy infusion) as long as the inequality is satisfied. It means that orderly product can be created out of irreversible process at the expense of generating dissipative entropy 



 n/
n/ ----- (7),
----- (7), 0, the entropy density s is a constant.
0, the entropy density s is a constant. , the whole system is at equilibrium
, the whole system is at equilibrium  .
. 0 ----- (9),
0 ----- (9),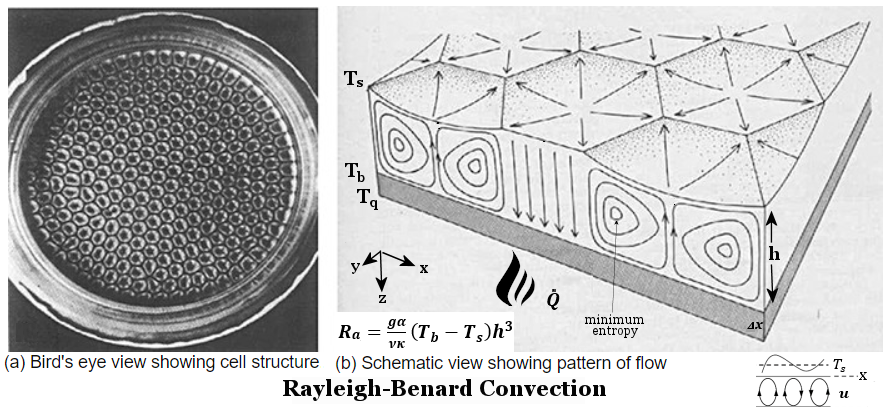


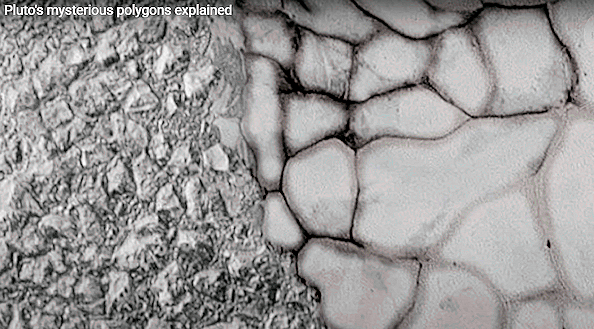

 dQ/T ----- (14),
dQ/T ----- (14),






 m Energy Flow (erg/s-g)
m Energy Flow (erg/s-g)




 Oxygenic atmosphere
Oxygenic atmosphere
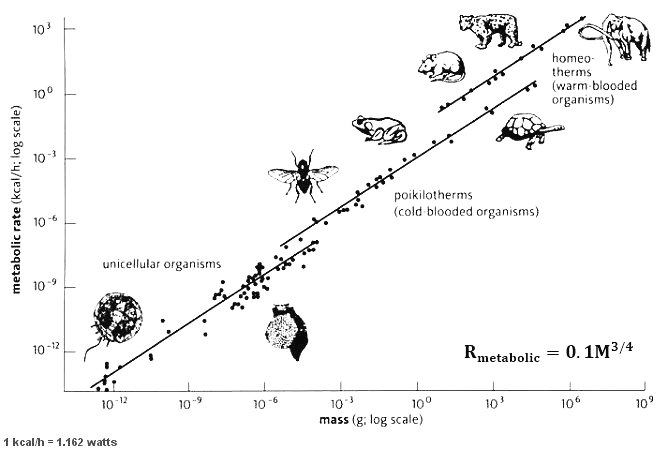
 can be calculated according to the formula shown in the Figure. This example illustrates different significance conveyed by entropy and information because they are related to
can be calculated according to the formula shown in the Figure. This example illustrates different significance conveyed by entropy and information because they are related to 


 (ni - 1), where N = 6.
(ni - 1), where N = 6.





 See
See 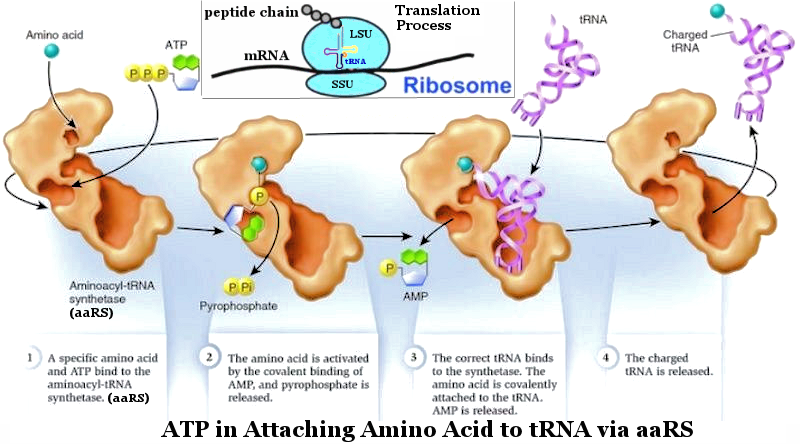

 ADP + Pi + 0.32 ev ----- (19).
ADP + Pi + 0.32 ev ----- (19).