Quantum Computing

Contents

Qubit and Entanglement

Physics and Computer science have combined to create a new field: quantum computing and quantum information. The spark that ignited world wide interest in this new field sprang forth in 1994 with Peter Shor's discovery of a theoretical way to use quantum mechanical resources to unravel a mathematical problem at the heart of electronic commerce and cryptography. Basic steps towards the creation of a quantum computer have been taken, with the demonstrations of elementary data storage and manipulation using photons and atoms or trapped ions as the quantum bits, or "qubits". Recently, it has been shown that it is possible to build solid-state qubits made from tiny samples of superconducting material. Figure 13-15 shows some of the subjects, which are currently being investigated in the field of quantum computing.

Figure 13-15 Qunatum Computing [view large image]

There are several requirements for a working quantum computer:


1. It must be scalable: it needs a set of qubits that can be added to indefinitely.
2. It must be possible to set all of the qubits to a simple initial state, such as all 0.
3. The interactions between qubits must be controllable enough to make quantum logic gates.
4. To perform operations using these gates, the decoherence times must be much longer than the gate-operation time (typically milliseconds to seconds).
5. There must be some readout capability.
6. To link up the computer's circuitry, it must be possible to convert memory qubits into processing qubits, and vice versa.
7. It must be possible to move processing qubits accurately between specified locations.

Qunatum computing exploits two resources offered by the laws of quantum mechanics: the principle of superposition of states and the concept of entanglement. Superposition is a "one-particle" property; while entanglement is a characteristic of two or more particles. Consider a particle with spin such as the electron. With reference to a given axis (say along the z axis), the spin of the particle can point in two opposite directions, say "up" and "down", and the spin states can be denoted as |1 and |0. But by the laws of quantum mechanics, the particle can exist in a superposition of these two states, corresponding to arbitrary orientation as shown in Figure 13-16.

Figure 13-16 Qubit [view large image]

Mathematically, the superposition of these two states can be written as: |f = a |1 + b |0 ------ (1) where a and b are related to the probability of finding the electron in state |1 and |0 respectively satisfying |a|2 + |b|2 = 1. This normalization defines the total probability of finding the electron to be 1. In general, the |1 and |0 states can be represented by any two-states entity such as "on" and "off", horizontal and vertical polarization of a photon, one particle vs no particle, ... etc.

|f is called a qubit. If a photon in state |f passes through a polarizing beamsplitter -- a device that reflects (or transmits) horizontally (or vertically) polarized photons -- it will be found in the reflected (or transmitted) beam with probability |a|2 (or |b|2). Then the general state |f has been projected either onto |1 or onto |0 by the action of the measurement (sometimes it is referred as collapse or decoherence of |f). Thus according to the rule of quantum mechanics, a measurement of the qubit would yield either |1 or |0 but not |f.(See Figure 13-16.)

		Now, consider a two-particle state: there are four "basis states", |11|12, |01|02, |11|02 and |01|12, where the subscript indicates particle 1 and 2. Again, superpositions can be made of these states, including in particular, the four "maximally entangled Bell states": |11|12 + |01|02 ------ (2) |11|12 - |01|02   ------ (3)
Figure 13-17 Entangle-ment [view large image]	Figure 13-18 Entanglement Implementation [view large image]	|11|02 + |01|12  ------ (4) |11|02 - |01|12   ------ (5)

Suppose particle 1 which Alice wants to teleport is in the initial state: |f1 = a |11 + b |01 ------ (6) and the entangled pair of particles 2 and 3 shared by Alice and Bob is in the state: |f23 = (|12|03 - |02|13)/21/2 ------ (7) which is produced by an Einstein-Podolsky-Rosen (EPR) source2. The teleportation scheme works as follows. Alice has the particle 1 in the initial state |f >1 and particle 2. Particle 2 is entangled with particle 3 in the hands of Bob. The essential point is to perform a joint Bell-state measurement (BSM)3 on particles 1 and 2 which projects them onto the entangled state:

Figure 13-19 Teleportation [view large image]

|f12 = (|11|02 - |01|12)/21/2 ------ (8)

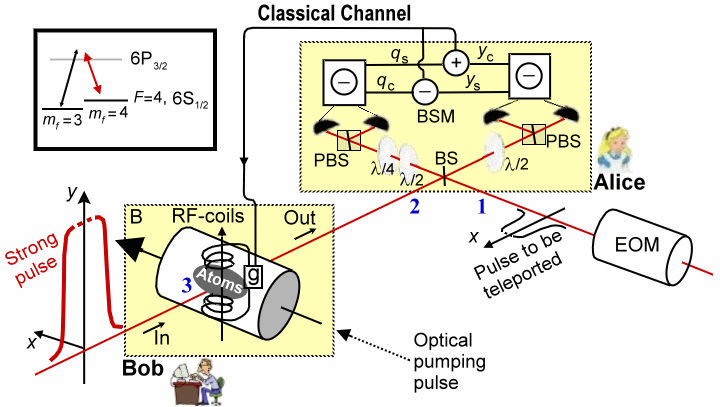
This is only one of four possible Bell states into which the two particles can be entangled. The state given in Eq.(8) distinguishes itself from the others by the fact that it changes sign upon interchanging particle 1 and 2. This unique anti- symmetric feature plays an important role in the experiment. According to the rule of quantum physics once particles 1 and 2 are projected into |f12, particle 3 is instantaneously projected into the initial state of particle 1. (See top portion of Figure 13-19.) This is because when we observe particles 1 and 2 in the state |f12 we know that whatever the state of particles 1 is, particle 2 must be in the opposite state. But we had initially prepared particle 2 and 3 in the state |f23, which means particle 2 must be in the opposite state of particle 3. This is only possible if particle 3 is in the same state particle 1 was initially. The final state of particle 3 is therefore: |f3 = a |13 + b |03 ------ (9) Note that during the Bell-state measurement particle 1 loses its identity because it becomes entangled with particle 2. Therefore the state |f1 is destroyed on Alice's side during teleportation. The transfer of quantum information from particle 1 to particle 3 can happen instantly over arbitrary distances,

hence the name teleportation. Experimentally, quantum entanglement has been shown to survive over distances of the order of 10 km. In the teleportation scheme it is not necessary for Alice to know where Bob is. Furthermore, the initial state of particle 1 can be completely unknown not only to Bob but to anyone. It could even be quantum mechanically completely undefined at the time the Bell-state measurement takes place. This is the case when particle 1 itself is a member of an entangled pair and therefore has no well-defined properties on its own. This ultimately leads to entanglement swapping (See lower portion of Figure 13-19). A complete Bell-state measurement not only give the result that the two particles 1 and 2 are in the antisymmetric state in Eq.(8), but with equal probabilities of 25% we could find them in any one the remaining three Bell states. When this happens, the state of particle 3 is determined by one of these three different states. Therefore Alice has to inform Bob, via a classical communication channel, which of the Bell state result was obtained; depending on the message, Bob leaves the particle unaltered or changes it to the opposite state. Either way it ends up a replica of particle 1. It should be emphasized that even if it can be demonstrated for only one of the four Bell states as discussed above, teleportation is successfully achieved, albeit only in a quarter of the cases.

Quantum Logic Processing

Factoring, Encryption, and Searching

Teleportation

polarizing beam splitters (PBS) for Bell-state measurement (BSM). The logic electronics identify the Bell state and convey the result through the microwave channel (RF unit) to Bob's electro-optic modulator (EOM). Depending on the message, it either leaves the photon state unaltered or changes it to the opposite state. Note that because of the reduced velocity of light within the fibre-based quantum channel, the classical signal arrives about 1.5 microseconds before photon 3. Thus, there is enough time to set the EOM correctly before photon 3 arrives. Polarization rotation (which introduces errors) in the fibres is corrected by polarization controllers (PC) before each run of measurements.

Figure 13-20a Teleportation over River Danube [view large image]

Polarization stability proved to be better than 10o on the fibre between Alice and Bob, corresponding to an ideal teleportation fidelity of 0.97.

Quantum teleportation has only been done between similar objects - from light to light or matter to matter until 2006, when the first step has been taken to teleport the quantum state between a photon and an atom. This technique is critical in transferring the light qubits into atomic storage. The experiment achieved only for a transmission distance of half a meter. The traveling distance can be extended with improvement on the control of signal degradation. Figure 13-20b shows the experimental set-up for the experiment. As usual, Alice is the keeper of particle (1) to be teleported, and the entangled particle (2); while Bob has the entangled particle (3) waiting to receive the teleportation. Here's the protocol:

Atoms are initially optically pumped into the F = 4, mF = 4 state with a 4-ms pulse (see insert). A 2-ms pulse of light is then sent through the atomic sample at Bob's location and becomes entangled with the atoms (3). The pulse travels 0.5 m to Alice's location (2), where it is mixed on a beamsplitter (BS) with the object of teleportation (1) - a few-photon coherent pulse of light - generated by electro-optical modulator (EOM). A Bell measurement is performed, and the results are sent via a classical communication channel to Bob. There they are used to complete the teleportation onto atoms by shifting the atomic collective spin state

Figure 13-20b Teleportation of Light to Atom [view large image]

with a pulse of radio-frequency (RF) magnetic field of 0.2-ms duration. After a delay of 0.1 ms, a verifying pulse is sent to read out the stomic state, in order to prove the successful teleportation.

Error Correction

Therefore, quantum error correction is performed differently as shown in the followings:
1. Prepare the primary physical qubit such as P = a |1 + b |0, which is to be protected from error.
2. Prepare two auxiliary A1, A2, which are then entangled (encoded) with the primary qubit to form a logical state.
3. Noise is applied to this logical state, which is represented by P, A1, A2 in Figure 13-21.
4. The primary qubit is decoded from the auxiliary qubits. Now P is separated from A1, A2.
5. Syndrome measurement is performed on the four possibilities for the auxiliary states A1, A2, e.g.,
   
   1. |1|1 for no error - association of the most often outcome with the most easily distinguishable measurement.
   2. |1|0 for auxiliary state 1 flipped - no correction required.
   3. |0|1 for auxiliary state 2 flipped - no correction required.
   4. |0|0 for primary qubit flipped - the primary qubit before correction is: P = -a |0 + b |1.
6. For the first and last cases, the original primary state has been altered. Appropriate correction is applied to recover the primary qubit initial state.

Such error-correction protocols have been implemented in 2004 using three beryllium atomic-ion qubits (the qubits comprise the two electronic ground state hyperfine levels, which are equated to the two spin 1/2 states - up and down) confined to a linear, multi-zone trap. The trap acts like a quantum register with the internal state of each ion playing the role of a qubit. It has been demonstrated that fidelity of 0.7 - 0.8 can be achieved in the experiments. However, the method works well only when at most one of the three qubits undergoes a spin-flip error. Figure 13-21 shows the transportation of the ions in the trap during the error-correction protocol as a function of time. Each experiment requires approximately 4 ms to perform. The ions are kept together by careful tuning of the phases of the optical-dipole force. Refocusing operations are required to counteract qubit dephasing caused by fluctuations in the local magnetic field.

Figure 13-21 Quantum Error Correction [view large image]

Data encryption is used to protect messages and files from prying eavesdroppers. In its simplest form, a coded message can be created in which each letter is substituted with the letter that is two down from it in the alphabet. So "A" becomes "C", "B" becomes "D", ... and so on. The recipient was told that the code (key) is: "Shift by 2". He/she can then decodes the message accordingly. Anyone else will only see a garbled message. Modern encryption employs two keys to provide greater security. The sender selects a public-key such as 1525381, which is the product of two prime numbers: 10667 and 143. This key is used to convert a block of text via an algorithm (a formula for combining the key with the text). The recipent must used a private key such as 143 to decode the encrypted text in the reverse process. The security of public-key cryptography depends on factorization - the fact that it is easy to compute the product of two large numbers but extremely hard to

Figure 13-22 Quantum Encryption [view large image]

factor it back into the primes. But the advent of the quantum information era - and, in particular, the capability of quantum computers to rapidly perform monstrously challenging factorizations - may portend the eventual demise of such cryptographic scheme.

Unlike public-key cryptography, quantum cryptography should remain secure when quantum computers arrive on the scene. One way of sending a quantum-cryptographic key between sender and receiver requires that a very low intensity laser transmits single photons that are polarized in one of two modes as shown in Figure 13-22. Followings illustrate the steps in establishing the key (see Figure 13-22):


1. Alice sends a photon through either the 0 or 1 slot of the rectilinear or diagonal polarizing filters, while making a record of the various orientations.
2. For each incoming bit, Bob chooses randomly which filter slot he uses for detection and writes down both the polarization and the bit value.
3. After all the photons have reached Bob, he tells Alice over a public channel, perhaps by telephone or an e-mail, the sequence of filters he used for the incoming photons, but not the bit value of the photons.
4. Alice tells Bob during the same conversation which filters he chose correctly. Those instances constitute the bits that Alice and Bob will use to form the key that they will use to encrypt messages.
5. If Eve the eavesdropper tries to spy on the train of photons, quantum mechanics prohibits her from using filters to detect the orientation of a photon. If she chooses the wrong filter, she will create errors by modifying their polarization.

Footnotes