Quantum Computing

Factoring and Encryption

Factoring is one of the hard problems that can be solved relatively easy by quantum computing. A number is factorizable if it can be produced by multiplying two or more integers greater than 1. Some number such as 2, 3, 5, 7, 11, 13, ... are not factorizable. They are called prime numbers. The result of multiplying two large prime numbers each with 200 digits is a 400 digits number. The run time increases linearly with additional number of digits. Thus, the forward operation is tedious, but the reverse becomes very difficult. It requires essentially the examination of all possible 200 digits numbers in turn until the one that can divide the 400-digit number. The run time now increases exponentially with additional number of digits until the resources reach a state of exhaustion for some large but finite number of digits. It is called intractable in technical jargon. One of the largest classical computations ever performed was factoring a 200-digit number a few years ago. It was shown in 1994 that even a relatively small quantum computer, with only a few thousand qubits, could factor a 400-digit number with ease via quantum parallelism. In the real world only the number 15 has been factored by a 7-qubit computer a few years ago.

Factoring large numbers is the basis for a powerful method of information protection. It utilizes a technique called public key cryptography. For example (see Figure 09), Alice sends a public key consisting of a large number (equals to the product of two smaller prime numbers) to Bob. Bob uses this public key to scramble or encode the returning message. Alice then decode the message with the private key consisting of the two original prime numbers. Since it is very difficult to factor the public key, the information is secure, that is, until the arrival of the quantum computing age.

Figure 09 Encryption

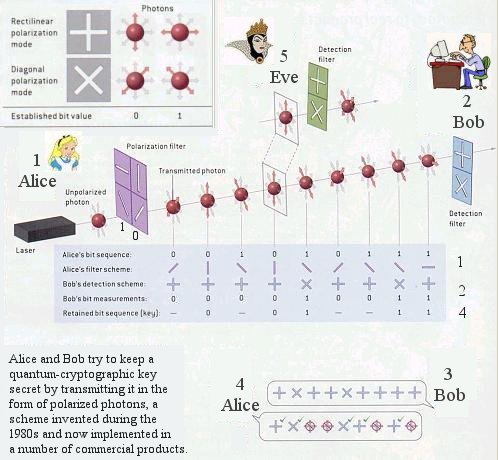Recalling that data encryption is used to protect messages and files from prying eavesdroppers. In its simplest form, a coded message can be created in which each letter is substituted with the letter that is two down from it in the alphabet. So "A" becomes "C", "B" becomes "D", ... and so on. The recipient was told that the code (key) is: "Shift by 2". He/she can then decodes the message accordingly. Anyone else will only see a garbled message. Modern encryption employs two keys to provide greater security. The sender selects a public-key such as 1525381, which is the product of two prime numbers: 10667 and 143. This key is used to convert a block of text via an algorithm (a formula for combining the key with the text). The recipent must used a private key such as 10667 to decode the encrypted text in the reverse process. The security of public-key cryptography depends on factorization - the fact that it is easy to compute the product of two large numbers but extremely hard to factor it back into the primes.

Figure 10 Quantum Encryption

But the advent of the quantum information era - and, in particular, the capability of quantum computers to rapidly perform monstrously challenging factorizations - may portend the eventual demise of such cryptographic scheme. (see footnote 3 for more detail of the public key security scheme).

Alice sends a photon through either the 0 or 1 slot of the rectilinear or diagonal polarizing filters, while making a record of the various orientations.
For each incoming bit, Bob chooses randomly which filter slot he uses for detection and writes down both the polarization and the bit value.
After all the photons have reached Bob, he tells Alice over a public channel, perhaps by telephone or an e-mail, the sequence of filters he used for the incoming photons, but not the bit value of the photons.
Alice tells Bob during the same conversation which filters he chose correctly. Those instances constitute the bits that Alice and Bob will use to form the key that they will use to encrypt messages.
If Eve the eavesdropper tries to spy on the train of photons, she may create errors when wrong filters are used to intercept the photons. The crucial safeguard is in hiding the key established by Alice and Bob.

Beginning in 2003, two companies introduced commercial products that send a quantum-cryptographic key beyond the 30 cm in the initial experiment. It has been shown that the use of fibre-optic cable can extend the transmission distance to 60-100 km. Other companies are trying to improve the products with transmission distance up to 150 km. The problem with transmission distance is related to the low laser intensity and the inability to use repeater (to amplify the signal). Similar to Eve's unsuccessful attempt, the repeater would introduce errors to the key.

In 2010 the two commercial quantum cryptographic systems have been hacked into successfully by researchers in universities. The scheme is for Eve to blind Bob's detector with a continuous, 1 milliwatt laser. The message is intercepted and re-sent as light pulses to Bob's detector, which is still functioning as

Figure 11 Quantum Encryption, Hacking

a classical detector receiving the pulse as a bit of 1 (Figure 11). He is entirely unaware that his detector has been sabotaged. The companies welcome the hacking as it will ultimately make the systems stronger.

China has launched a "quantum satellite" on August 16, 2016 (Figure 12a). It carries three experiments on board - the quantum encryption, entanglement, and teleportation. All of them are the extension of ground based testings to outer space about 500 km above ground. The environment is much more suitable but it requires very precise aiming at such long distance and with moving object. The satellite

Figure 12a Quantum Satellite {view large image]

goes by the name of Mozi (墨子) - the ancient sage reputed to be the first Chinese optician some 2500 years ago. The mission will run for 2 years; many more will follow to organize secure communications throughout the world. See "量子科學實驗衛星".

2020 Update :

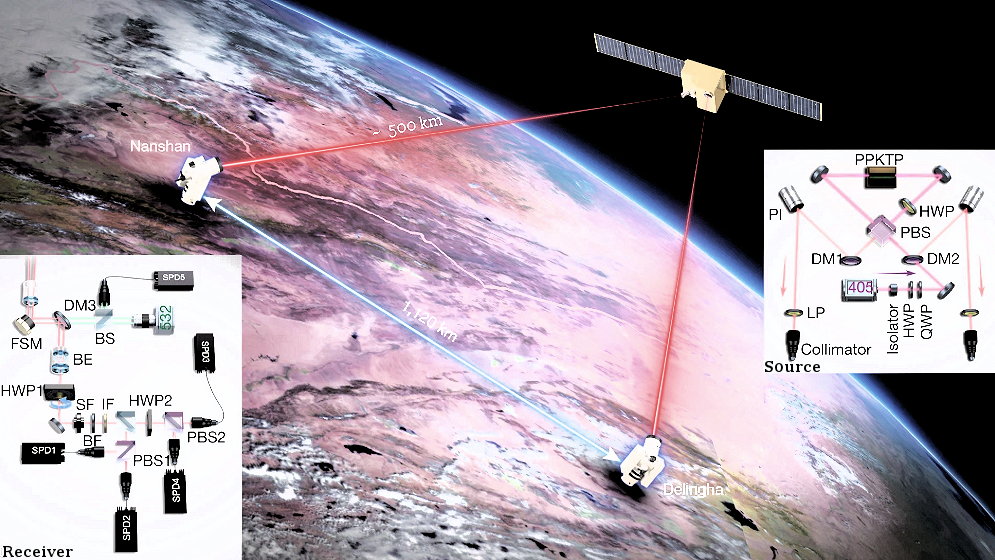		In 2020, an experiment with entangled photons achieves a break-through in Quantum Key Distribution (QKD) implementation. The satellite was able to send the entangled pair to 2 ground states 1120 km apart (Figures 12,b,c). They are actually 1.2 m diameter telescopes stowed with advanced optical instruments. The result demonstrates the feasibility of long distance QKD operation secured from prying eyes.
Figure 12b Quantum Satellite, Mozi [view large image]	Figure 12c Mozi QKD [view large image]	See original article "Entanglement-based secure quantum cryptography over 1,120 kilometres", and "量子密鑰有新解方".

Firstly, an exposition on entanglement specially tailors for the Mozi experiment :

When 2 particles with individual state |0> and |1> respectively merge together, they become one system with state |01> or |10>. These 2 particles are said to be entangled. They can be separated later but still trying to maintain the unity before collapsed (un-entangled) by interaction with other particles in the environment. Practically, the creation of entangled photons is by the process of generating ultra-violet photon in higher energy state (the united state); occasionally it would split into 2 lower energy photons of blue and red color, in different polarizations and entangled (Figure 12d).

Figure 12d Entanglement

Figure 12e,a shows the formula and symbols for 2 entangled photons. Photon #1 is denoted in dark color, #2 in red. It is for entanglement of horizontal (0) and vertical (1) polarizations. The first letter in the symbol is for photon #1, the second for #2.

The entangled photons are separated by a "Polarized Beam Splitter (PBS)" as shown in Figure 12e,b. They are sent over to 2 observers respectively.

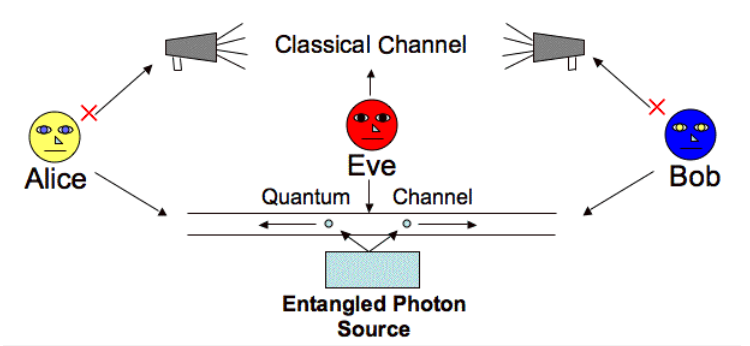
Figure 12e from Entanglement to Measurement [view large image]

The photons collapse (un-entangled) upon measurements by one of the observer resulting in random sequence of horizontal and vertical polarizations, i.e., in binary sequence of 0 and 1, and the opposite sequence of 1, and 0 for the other observer (Figure 12e,c). This is the thoroughly randomized Quantum Key.

This kind of quantum key (the sequence of 0 and 1 mentioned above) is supposed to be more secure than factoring in quantum computing age. However in earlier days (20th century), the sender has to inform the receiver which one of the 4 maximally entangled Bell states (Figure 12e,d) is used via a classical channel involving further security risk. The Mozi experiment avoids such complication by using a fixed Bell state in generating the entanglement.

Quantum key distribution (QKD) is only used to produce and distribute a key (something like a password), not to transmit any message or data. This key can then be used with any chosen encryption algorithm to encrypt (and decrypt) a message, which can then be transmitted over a standard communication channel.

The source in the satellite delivers about 6x10⁶ entangled photon pairs per second (about 100 times the brightness of dimmest star), but the ground stations receive only 0.12 bits per second. Most of them have collapsed during the flight because the distance from ground stations to satellite is about 500 km making a flight time of about (5x10⁷ cm) / (3x10¹⁰ cm/sec) ~ 10^-3 sec, while the decoherence time for the photon pairs is about 10^-4 sec. Thus, most of them have already collapsed before reaching the ground.

Anyway, the experiment involves precision targeting, it should have no problem with application for funding.

Entanglements are verified by coincidence circuit, which has a time resolution of about 10^-9 sec. They measured violation of "Bell's Inequality" with S ~ 2.56 > 2 (see Eq.(7) in "Bell's Theorem") proving that the pairs are entangled and incidentally the "Quantum Theory is correct".

This method does away the notification via classical channel (for Alice to inform Bob about which Bell state being used) by selecting one of the 4 "maximally entangled Bell states" at the source. It also doesn't need relays to maintain the signal strength. It is thus more secure from Eve's prying eyes. Any attack will be discovered swiftly as it would collapse the entanglement (Figure 12f). See "The World's First Quantum Science Experiment" for more details.

Figure 12f[view large image] Mozi Entanglement Exp.

The team leader is Jianwei Pan (潘建偉). His PhD thesis adviser is Anton Zeilinger of the University of Vienna, the one who sent entangled photons across the Danube in 2004. It is no accident that Vienna is the only ground station outside China to run Mozi experiments.

Leading China's Quantum Computing Mission

³Public Key Security Scheme

Instead of relying on the password scheme, the public-key authentication is now used by financial institutions and communication providers for better network security. Followings describe briefly the main components to implement such system.

1. Public-Private Keys - As mentioned in the main text, the security relies on the private key, which is used for decryption and is

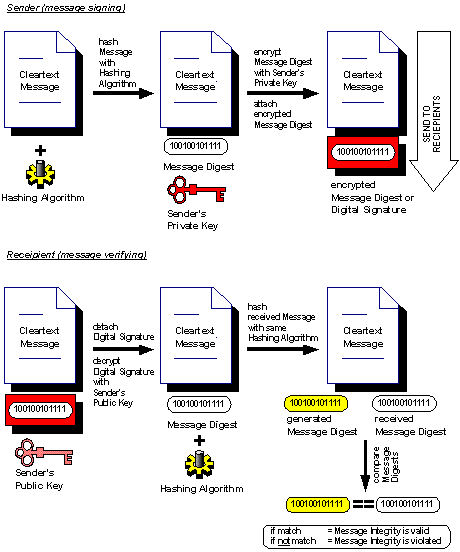		known by the recipient only. The two keys are given (by the web hosting company for example) in the form of exponents (two different prime numbers, a shorter one for the public key, a longer one for the private key) and a common 1024 bits modulus. 2. Certificate Authority - The keys alone do not guarantee secure communication unless it can prove the owner's identity without doubt. This is the role played by the certificate authority (CA), which is (similar to the passport office) the agent to certify the credential of the keys. As shown in Figure 14, the public key together with other information are submitted to the registration authority (RA),
Figure 14 Certification Processing [view large image]	Figure 15 Hashing [view large image]	who in turn obtain the certificate from CA. The owner of the keys can now execute transactions without arousing suspicion from the other end.

3. Hashing - Even though a document has been encrypted, another layer is added to ensure it is sent off by the right person, i.e., a digital signature is required. The scheme is to generate a single unique large number (called a hash) by running the file through a complicated mathematical computation with the sender's private key. Upon receiving the file, another hash number is generated using the sender's public key. If the hashes match, the data were not tampered with and the sender's signature is on it (Figure 15).
4. An example - When a user logs on to the website of a bank, the very first thing unusual is the website's URL (see above) - its beginning is "https" instead of the more familiar "http" and sometimes the URL address bar shows a bright green color. The "s" in "https" indicates that the site has implemented the HTTP Secure protocol. Pointing the cursor to the "lock" icon at the end would show information about the CA etc. At the opening of the homepage, the user receives a public key along with all the data that his/her web browser displays. Then the data entered to the page will be encrypted by the bank's public key and decrypted at the other end by the bank's private key. The key and encryption stay in the background without the user's notice, i.e., the security processing is transparent to the user.