Graphene

Contents

Nature of Carbon Atoms

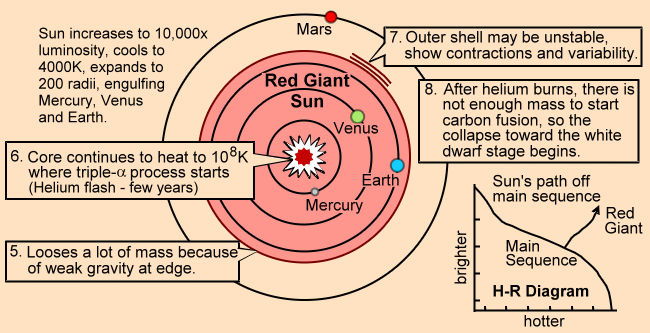
			Carbon atoms are made in the Red Giant phase of stellar evolution by the triple alpha process (Figure 01) in the core. Figures 02, 03 depict a series of steps leading up to such stage (also see "Origin of Elements"). Most of the elements in the star are
Figure 01 Carbon Generation [view large image]	Figure 02 Red Giant Phase [view large image]	Figure 03 Helium Burning [view large image]	eventually thrust into space by blowing stellar winds or ejected during supernova explosion.

		The nucleus of carbon atom has 6 neutrons (N) and 6 protons (P) with 6 electrons moving around outside - 4 of them are valence, chemically active (the two 1s electrons are inert in a complete shell further inward). At ground state, the configuration is in the form of 1s22s22p2, where the leading numeral is the principle quantum number n, s and p are the orbital quantum numbers with = 0 and 1 respectively, while the superscripts represent the number of electrons in that particular level (each level, e.g., s or px can accommodate at most two electrons with opposite spin orientation, see Figure 04).
Figure 04 Carbon States [view large image]	Figure 05 Hybridization of CO2 [view large image]	Energy of the electrons are determined mainly by n with small variation due to other quantum numbers or via external interaction. For example, combination with other atom(s) will change the energy level and configuration in a process called hybridization.

Graphene Structure

		The structure of graphene is a two dimensional version of the carbon allotropes (Figure 06). Each individual atom possesses three sp2 orbitals which interact with the other ones in its neighborhood to form covalent sigma bonds; while the 4th orbital maintains a weaker van de Waals pi bond for stacking up the layers to form graphite (Figure 04). In single layer, the electrons in the pi bonds link up together to form valence and conduction bands. The bands at the edge of the sheet make contact with each other in
Figure 06 Hexagonal Lattice of Graphene [view large image]	Figure 07 Graphene in k-Space	6 points (the Dirac cones) at the boundary of the first Brillouin zone (the hexagon in Figure 07) contributing some weird electronic properties as shown later.

where vF ~ 108 cm/sec is the velocity of the electron corresponding to the Fermi energy, and the Pauli matrices. Thus, the dependence on k becomes linear instead of quadruple. The deviation is caused by the spin-orbit interaction at such location. It is derived from a phenomenological (empirical) model for spin-orbit coupling. The spin in this case is actually pseudo-spin identified to the valence and conduction bands respectively for spin up and down. Pseudo-spin is a term applicable to all kinds of objects having two different properties, e.g., the iso-spin associated with proton and neutron, ... etc. Comparison of such Hamiltonian H by the massless Dirac (Weyl) equations below shows that it is just the same equation with the speed of light c replaced by vF, where E = c|p| = |p| (for c = 1 in natural unit) :

Figure 08 Dirac Cones, Formation

This superficial resemblance underlies the oft quoted statement that the electron becomes massless in graphene. However, massless particle always moves at the velocity of light (not just vF) according to Special Relativity.

Graphene Properties

Some of the graphene properties related to its unique structure are listed in the followings :



Mechanical - The strong covalent sp2 bonds endows an exceptional tensile strength of more than 100 GPa for the graphene (stainless steel has about 0.5 GPa, see table for "Propertie of Metallic Solids"); while the weight of the graphene sheet is very light at about 10-3 gm/m2. The Young's modulus for graphene is about 1.0 TPa (better than the 0.2 TPa for steel ) implying an elastic property of high resistance to deformation (Figure 09,a).

Figure 09 Graphene Properties [view large image]

The Young's modulus E is related to the spring constant k by the formula : k = E(A/L) where A and L are the cross-section and length of the object respectively.



• Electrical - Graphene displays remarkable electron mobility at room temperature in excess of 15000 cm²/V-Sec. The corresponding resistivity (inverse of conductivity) would be 10^-6 Ohm-cm - about the same for silver or copper (see "Propertie of Metallic Solids"). This unique property is due to the long mean-free-path of the order of 65 x10^-4 cm (Figure 09,b).



Electronic - The electronic properties of graphene are dictated by the valance and conduction bands made up by the pi orbitals (Figure 06). Since the density of states (DOS) for prefect graphene is zero at the Dirac points, electronic conductivity is actually quite low. However, the Fermi level can be changed by defect or doping (creating free electrons or holes, see Figure 10) to make it better at conducting electricity than, for example, copper at room temperature. A notable feature on graphene transistors is its ability to continuously varying the resistivity by controlling the back gate voltage to permit the absorption of oxygen molecules onto the device (see "Oxygen Adsorption in Graphene").

Figure 10 Graphene Density of State (DOS) [view large image]

The "Back Gate Voltage" induces change in the Gate Voltage by an amount approximately equal to the change in the source voltage (Figure 09,c).



• Chemical - Perfectly flat graphene is chemically inert. Thus, chemical applications of graphene need either structural or chemical irregularities. Graphene is commonly modified with oxygen- and nitrogen-containing functional groups. The onset temperature of reaction between

  graphene (with defects) and oxygen gas is about 530 K. It combusts at 620 K. Graphene melts into an agglomeration of loosely coupled doubled bonded chains at about 6000 K (see melting point for other allotropes at 3800 K in "Properties of Non-Metallic Solids"). Graphene sheet is thermodynamically unstable if its size is less than about 20 nm. A stable structure requires about 6000 atoms, and it becomes the most stable for layer larger than 24,000 atoms.

  Figure 11 Graphene Oxide (GO) [view large image]

  Graphene oxide (GO) is an important precursor to graphene and has many promising characteristics itself (Figure 11, also see "Properties and Applications of Graphene Oxide"). Its product of photolysis (by sunlight) could persist for a long time posing certain environmental risk (Figure 09,d).

• Thermal - Thermal conductivity measurement shows an exceptionally large thermal conductivity of between 1500 - 2500 W/m-K for suspended single layer graphene - much higher than even the copper's 385 W/m-K (see "Propertie of Metallic Solids"). Squeezing (or clamping) graphene can reduce heat flow from hot to cold place (Figure 09,e). This property could have many applications to direct where excessive heat should go (see "Squeezing Graphene is A Way to Control Graphene Heat Conduction").


• Optical - In general, 2.3% of the white (visible) light is absorbed by graphene (widow glass absorbs 10-20%). This number has a theoretical base relating it to the fine structure constant by = 3.1416x(1/137) = 0.023 (see "Fine Structure Constant Defines Visual Transparency of Graphene"). The absorption becomes saturated when the input optical intensity is above a threshold value.

  At THz range (100 THz - 1 GHz, Figure 12,c) in the presence of a bias magnetic field and three layers of graphene, the left-handed circular polarized light (LCP) is reflected, while the right-handed one is absorbed by the graphene (Figure 12,a). A device has been fabricated with such characteristic in 2016 (see "Graphene THz Isolator"). It is an useful example for protecting the input of certain electro-magnetic wave with special property from interference by other kind of em waves. The additional significance of the design is the currently empty THz frequency range, leaving the potential of the unexploited THz band for Optic Fiber data transmission in the future. Figure 12,b is from another research to simulate the LCP reflection in the 1 THz range (see "Circular Polarization Absorbers with Graphene").

  Figure 12 Graphene Isolator [view large image]

  BTW, circular polarized light always changes handedness upon reflection (see "Circular Polarization"), also see "Electromagnetic Spectrum" for another display of the frequency range.

• Superconductivity - The March 2018 publication on graphene bilayer (Figure 12a,a) indicates that misaligned of the two sheets by 1.1^o could transform it into superconductor. Followings are summary of the finding and some comments.
  
  
  • As indicated in "Graphene Structure", there are six points in the k-space (at the edge of the sheet), where two conic shape bands are in point contact. They can be considered as two iso-spin states, i.e., up and down (iso-spin or pseudo-spin is a term applicable to all kinds of objects having two different properties, e.g., the iso-spin associated with proton and neutron, ... etc). The hexagon confined by these points is called the 1st Brillouin zone within which the electrons are moving freely and have the same energy (Figure 12a,c).
  
  
  • It is known for sometimes that novel electronic properties would emerge when two sheets of graphene is offset by certain angle (Figure 12a,b). Initial experiment by twisting the bilayer with offset at a magic-angle yields a Mott insulator indicating strong Coulomb interaction between electrons (called correlation in the trade), which is usually neglected in the first approximation.
  
  
  • By introducing doping into the system at this particular offset angle of 1.1^o, the bilayer turns into a superconductor at 1.7 K. There is a video to show the conduction and valence bands in the graphene structure gradually collapsing into an extremely flat band in the 1st Brillouin zone at a particular energy leve (Figure 12a,d).
  
  
  • This kind of superconductor has many properties similar to the cuprates (an un-conventional "high temperature - up to 133 K" superconductor) including :
    • Cuprate superconductors are 2D materials with their superconducting properties determined by electrons moving within weakly coupled copper-oxide (CuO₂) layers. Neighbouring layers containing ions such as lanthanum, barium, strontium, or other atoms act to stabilize the structure and dope electrons or holes onto the copper-oxide layers. The undoped "parent" or "mother" compounds are Mott insulators.
    • Existence of strongly correlated insulating state very close to superconductivity is the hallmark of unconventional superconductors.
    • Similar phase diagram as shown in Figure 12b.
    • Although the critical temperature for bilayer graphene is still very low at 1.7 K, it is achieved at an usually low electron density at about 1/1000 that for conventional superconductor suggesting that the interaction at play should be much stronger.
  
  
  • The mechanism to generate un-conventional superconductivity remains unknown for the last 30 years (see "Superconductors across the Decades"). The bilayer graphene superconductor is easier to manipulate providing a highly tunable platform with which to investigate such phenomena.
  
  
  • The video on the transformation of the bilayer to superconductor shows the collapse of the conduction and valence bands into an extremely flat band. It implies that all the states in these two bands have degenerated into one energy level. If we regard the states in the conduction band as iso-spin up and those in the valence band as iso-spin down, then the respective electrons in the flatten band would tend to pair up according to the Hund's rule as shown in Figure 12c. Such pairing would produce a boson (either with "real" spin 0 or 1), which is responsible for the superconductivity as prescribed by the BCS theory. This scenario to produce "high temperature" SC would require a much stronger inter-iso-spin interaction than the one forming the Cooper pair. (???)
  
  

  Figure 12a Superconductivity [view large image] and [see video on the transformation to superconductivity]	Figure 12b Cuprate Doping [view large image]	Figure 12c Pairing of Opposite Spins

  See original article in "Surprise Graphene Discovery could Unlock Secrets of Super-conductivity", Nature News, 05 March 2018.

  [Top]

  ---

  Applications

  Since the successful isolation of graphene in 2004, the number of related publications has skyrocketed from the initial few to about 16000/yr in 2013 (Figure 12d,a). There are corresponding increases in utilizing its special mechanical, electrical, ... properties to all kinds of applications as shown in Figure 12d,b, and Table 01 below. However, only a few have advanced to the status of commercialization. One of the problems is scalability.

  Theory or laboratory testing may look promising, but it is difficult to translate the idea to industrial level without compromising its properties. It is often said that similar to the "age of plastic" in the 20th century, the 21st century belongs to the graphene, i.e., it would be the "age of graphene". Actually, critical assessment should be conducted to evaluate its impact on the environment (see "Toxicity"). It would be a nightmare to see the globe covered with discarded graphene sheets which are invisible, electrical conductive and have the strength to withstand destruction.

  Figure 12d Age of Graphene [view large image]

  
  

  Application	Comment	Status
  Batteries	Improved performance with the incorporation of graphene	Huawei Prototype (2016)
  Bio-sensor	Sensitive graphene transistor to detect bio-molecules	Glucose sensor prototype (2015)
  Catalyst	Speeding up the rate of chemical reactions	Evaluating (2014)
  Conductive Ink	Electricity conduction on paper and other materials	Available since 2009
  Contrast Agents	For MRI imaging	Research report (2013)
  Coolant additive	Enhancing the thermal conductivity of a base fluid	In development (2013)
  Data Storage	Million-fold improvement over current hard drives	Research report (2015)
  Drug Delivery	Used as theranostic probes targeting magnetic, infrared, ... sources	Under investigation (2016)
  Graphene Filters	Filtering salination, molecules, contamination, unwanted radiation	In various research stages (2017)
  Graphene Coating	Graphene composites on all kinds of surfaces giving novel functionalities	Limited commercialization (2017)
  Graphene Quantum Dot (GQD)	With size < 30 nm, for biological, opto-electronics, energy, ... applications	For sale (2017)
  Lubricant	To replace the traditional graphite	Studied in 2014
  Magnetic Sensor	Based on Hall Effect	In lab testing stage (2015)
  Nanoelectromechanical systems	Nanoscale devices integrating electrical and mechanical functionality (NEMS)	In development (2012)
  Optical Modulator	Use Fermi level tuning to achieve high modulation speed, large bandwidth	Demonstrated (2011)
  Photodetector	Superior performance by coupling with silicon quantum dots	Demonstrated (2016)
  PCR Enhancement	Enhancing accuracy of DNA sequencing with graphene oxide	Investigated (2016)
  Redox	Controlable reduced/oxidized states via electrical stimulus in GO	Demonstrated (2011)
  Smart Window	Opaque window turns transparent by applying an electric field	In development (2016)
  Solar Panel	Graphene Oxide (GO) and other compounds may be the better choice	In various research stages (2017)
  Spintronics	Used in disk drives, random-access memory, and computer processor	Research report (2015)
  Supercapacitor	Comparable to current lithium-ion batteries	Demonstrated (2015)
  Thermoelectrics	Converting heat into electricity	Reported (2015)
  Tissue Engineering	Improvement of mechanical properties.	Under investigation (2013)
  Transistors	Replacing silicon in transistors by graphene	Under investigations (2015)
  Transparent Electrodes	In touch screens (see video), liquid crystal displays, organic photovoltaic cells, and organic light-emitting diodes	Introductory phase (2016)
  Super-elasticity in Deep Freeze	The elasticity over wide temperature range could make it useful in extreme environments such as outer space.	Research report (2019)

  Table 01 Graphene Applications

  A 2016 survey indicates that the most-mentioned graphene topic in that year is "Composites". This is a relatively simple application by mixing graphene with a certain product creating novel functionality such as the graphene ink. The process is sometimes referred as functionalization, which creates new functions, features, capabilities, or properties via mixing two things. See various kinds of startups chart in 2011, 2014 perspective on "Graphene Applications", 2015 version, 2016 survey, 2017 news, the future up to 2035, and graphene products for sale now from "Graphenea".

  [Top]

  ---

  Production

  		There are many methods to produce graphene sheets (Figure 13). In the 2012 review article "A roadmap for graphene" only those scalable for industrial use are listed (as shown here in Figure 14,a). This is an excellent review on other aspects of graphene as well. A summary from the review for such production methods is provided below.
  Figure 13 Graphene Production	Figure 14 Graphene Production, Scalable [view large image]

  Liquid Phase Exfoliation (LPE) - This is the cheapest way to produce graphene or graphene oxide flakes of low quality. The process involves dissolving graphite or graphite oxide in a solvent, then uses some kinds of agitation (such as sound wave) to shake loose the layers into two dimensional platelets (Figure 15). The method is said to be as simple as running it with a kitchen blender. Anyway such low grade graphenes are already available on the tonne scale for sale in the market and produce composite applications such as graphene-based inks, ... by 2014.

  Figure 15 Graphene Production, LPE [view large image]

  
  
  • Chemical Vapor Deposition (CVD) - The process is similar to the soot formed on the cover of a burning lamp. The modern version is to deposit vaporous carbon atoms on copper foils (Figure 16,a) and then transferred the graphene sheet to a dielectric substrate. The process is expensive owing to large energy consumption to remove the graphene layer from the underlying metal substrate. There are also requirements to

    	control the (grain) size, ripples, doping level and number of layers, ... This technique has been used to produce transparent conductive coating applications (such as touch screens). The process can be improved by adopting novel technique such as "Plasma-Enhanced CVD (PECVD)", in which the precursor is ionized into plasma, and the substrate can be SiO2/Si (Figure 16,b).
    Figure 16 Graphene Production, CVD and PECVD [view large image]

  
  
  • Synthesis on Silicon Carbide (SiC) - This method grows graphene on top of either face of the silicon carbide sheet at high temperature (above 1,000 C). Apart from the high temperature required for growth, there are other issues of small size of the crystallites and unintentional doping from the substrate and buffer layers.
  
  
  • Mechanical Exfoliation - This method pulls apart the multi-layered graphite until the last single one, which is the graphene (Figure 14,b). The product is then ransfered onto a SiO₂ substrate. The process is called exfoliation for peeling off a 2-D layer from 3-D object. It is essentially the way to isolate the first graphene flake from pencil using Scotch tape. The process is slow and limited in size making it expensive and suitable only for research and prototyping.
  
  
  Other Methods :
  
  
  • Molecular Assembly (Molecular beam epitaxy) (Figure 14,b) - Successful growth has been reported on both the carbon and silicon terminated faces of silicon carbide substrates in the temperature range 1000-1100 C from a solid carbon source. Similar successes have also been achieved on different kinds of substrates. But it is unlikely to be used on a large scale because of its much higher cost than the CVD method.
  
  
  • Anodic Bonding (Figure 13,b) - This method produces graphene sheets on a glass substrate with the anodic bonding method, in which a graphite precursor in flake form is bonded to a glass substrate with the help of an electrostatic field and then cleaved off to leave few layer graphene on the substrate. It is simple and practical for producing graphene samples of size ~ 0.01 cm.
  
  
  • Photo Exfoliation (Figure 13,c) - This method uses an infrared laser to alter the orbital structure of the carbon atom from sp³ to sp² in 3-dimensional networks of graphene layers from commercial polymer films. The laser-induced graphene (LIG) exhibits high electrical conductivity and can be readily patterned to interdigitated electrodes for in-plane microsupercapacitors. The technique provides a rapid route to polymer-written electronic and energy storage devices.
  
  
  • Precipitation from Metal (Figure 13,f) - The technique dissolves carbon source in molten metal at high temperature and the extracts the graphene upon rapid cooling (before the formation of graphite). It is observed that roughly half of the carbon source is crystallized into graphene with the rest either outgassing from the system or remaining in the metal film.
  
  
  • Chemical Synthesis (Figure 13,i) - This method consists of the synthesis of graphite oxide, dispersion in a solution, followed by reduction with hydrazine (N₂H₄). But when the size of the end product (the graphene) is larger than about 1 nm, it usually ended up with defects ruining its many wonderful properties. A procedure has been demonstrated in 2013 to bypass the problem that allows the synthesis of graphene from GO with the carbon skeleton preserved in the order of tens of nanometer. The steps are essentially those depicted in Figure 11.
  
  

  [Top]

  ---

  Identification

  At the end of the production process it is necessary to check out the quality of the product. As shown in Figure 17,a the visual image from naked eye reveals no characteristic that can identify the substance to be really the graphene, additional step is required to certify the authenticity of the product. Followings are some of the methods that can be used to complete the production cycle.
  
  
  • Transmission Electron Microscopes - Since the length scale of graphene's hexagonal structure is about 10^-7 cm, it requires a microscope of about 10⁶X magnification to reveal a viewable image. The maximum magnification of 10³X by compound optical microscope is obviously not sufficient. The scanning electron microscope can provide 10⁵X, which barely shows the ripple of the underlying substrate and the darker

    	contrast of the bilayers (Figure 17,b). Only the transmission electron microscope with magnification up to 5x106X is capable to show the graphene structure in detail (Figure 17,c). See "Electron Microscopes" for a brief introduction of the instruments.
    Figure 17 Graphene Imagings [view large image]

    
    

    Raman Spectroscopy - It forms when the incident light (e.g., in the form of laser) with wavelength about 500 nm (in the infrared range) interacts with certain material, which re-emits radiation with wavelength above and below the incident value according to whether the final vibrational energy level is higher or lower (see Figure 18,a for the corresponding Stoke or Anti-Stoke scattering). The process can be considered as inelastic scattering which occurs some 107 times less than the elastic (Rayleigh) scattering with no change in wavelength (Figure 18,a,b). The virtual energy level in the process materializes only for a very short interval following the rule of the Uncertainty Principle.

    Figure 18 Raman Spectrum of Graphene [view large image]

    The Raman spectrum of the graphene originates from the vibrational transition of the sp2 carbon atoms (see Figure 06). In addition to identify the presence of graphene, the two or three emission bands (instead of lines for isolated atom) can be used to decipher the number of layers in the substance :

    	2D (G') Band - This band is unique for single layer graphene at about 2650 cm-1. Its intensity decreases with increasing number of layers (Figure 18,c), the band width is also broaden correspondingly. It is not affected by proximity to a defect. The process involves the creation of electron/hole pair in the Dirac cone K and ends up with its annihilation at K' cone (Figure 19).
    Figure 19 Process for Graphene 2D Band Generation [view large image]	G Band - This band is at about 1583 cm-1 and occurs most prominently in graphite. The ratio of G/2D intensity is a good indicator for the presence of either kind (Figure 18,c). The G band arises from the stretching of the C-C bond.

    • D Band - This band occurs only when either the graphene or graphite has defect within, such as GO (graphene oxide) or rGO (reduced graphene oxide) as shown in Figure 18,d. In other word, this band originates from the disordered structure of graphene.
    
    

    Total Color Difference (TCD) - This method bases on the concept of color space, which is an attempt to quantify the subjective color perception by each individual. For example, the spatial x, y, z axes can be replaced by RGB (Red, Green, Blue) each has 256 discrete levels for a total of 256x256x256 = 16.7 million colors. The CIELAB color space (as shown in Figure 20, where L* represents neutral color (~ brightness), a* from green to red, and b* from blue to yellow) is device independence. This means that the colors are defined independent of their nature of creation or the device they are displayed on.

    Figure 20 Color Space and TCD [view large image]

    Similar to the distance defined between two spatial points, the Total Color Difference (TCD) E*ab between two different colors can be defined in color space (see formula in Figure 20).

    
    For example, a standard light source produces a specific point p₁ in the color space for a certain substance, then another point p₂ for an unknown substance; the two substances are the same if E*_ab ~ 0. The TCD becomes large when the substances are not the same (see the scale on the right of Figure 20). In this way we can identify an unknown specimen to a standard substance - the graphene in this case. This method

    		has been demonstrated for identifying graphene accurately in 2008 (see Figure 21, also "Total Color Difference for Rapid and Accurate Identification of Graphene"). A 2013 update uses contrast difference as shown in Figure 22, in which the numerals indicate the layer numbers while the contrast difference is computed from CD = C - Cs, where C is the contrast of the MoS2 nanosheet and Cs for the SiO2/Si substrate.
    Figure 21 Graphene TCD [view large image]	Figure 22 Contrast Difference [view large image]	See original article "Rapid and Reliable Thickness Identification of Two Dimensional Nanosheets Using Optical Microscopy".

    BTW, contrast is determined by the difference in the color and brightness of one object and other objects within the same field of view.
    
    
  • Other Methods - Graphene can also be identified by checking out the electrical or thermal property of the substance. However, it may not be very reliable as the material can be something else with the same kind of property.
  
  Anyway, this is definitively not the end of the story for graphene. There would be updates for the years to come.