 |
which is in the same form as Eqs.(1a,b) for the 2-dimensional rotation, but in the (fR, fI) complex plane with the real and imaginary parts of the function as coordinates (Figure 01f). This plane is called an internal space, and the associated symmetry an internal symmetry, if the mathematical formulation is unchanged after the operation. For example, fR and fI can be identified to the two components of the scalar field in the Klein-Gordon Equation, e.g., 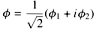 . The internal rotation just presents different aspect of the field components in the complex plane. The Klein-Gordon Equation is invariant (unchanged) under such internal rotation, which is another way to say that the equation is symmetrical with respect to such operation. It is obvious from Figure 01f that length of the arrow has not changed by merely rotating the complex plane. It is something like renaming a person from John to Jack - that person remains the same although there may be some legal or financial consequences. The analogy in Figure 01f can be taken with the "arrow" as the person, f and f ' as the different names. . The internal rotation just presents different aspect of the field components in the complex plane. The Klein-Gordon Equation is invariant (unchanged) under such internal rotation, which is another way to say that the equation is symmetrical with respect to such operation. It is obvious from Figure 01f that length of the arrow has not changed by merely rotating the complex plane. It is something like renaming a person from John to Jack - that person remains the same although there may be some legal or financial consequences. The analogy in Figure 01f can be taken with the "arrow" as the person, f and f ' as the different names.
|

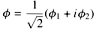 . The internal rotation just presents different aspect of the field components in the complex plane. The Klein-Gordon Equation is invariant (unchanged) under such internal rotation, which is another way to say that the equation is symmetrical with respect to such operation. It is obvious from Figure 01f that length of the arrow has not changed by merely rotating the complex plane. It is something like renaming a person from John to Jack - that person remains the same although there may be some legal or financial consequences. The analogy in Figure 01f can be taken with the "arrow" as the person, f and f ' as the different names.
. The internal rotation just presents different aspect of the field components in the complex plane. The Klein-Gordon Equation is invariant (unchanged) under such internal rotation, which is another way to say that the equation is symmetrical with respect to such operation. It is obvious from Figure 01f that length of the arrow has not changed by merely rotating the complex plane. It is something like renaming a person from John to Jack - that person remains the same although there may be some legal or financial consequences. The analogy in Figure 01f can be taken with the "arrow" as the person, f and f ' as the different names.
 t), then a is just the phase shift of the wave. The phase shift interpretation provides another representation other than the rotation in the complex plane as introduced in the followings.
t), then a is just the phase shift of the wave. The phase shift interpretation provides another representation other than the rotation in the complex plane as introduced in the followings.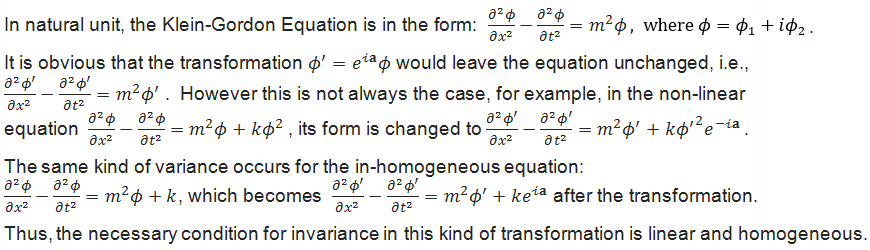
 f '
f '  0. Since the phase angle can be infinitesimally small, this kind of group also belongs to the Lie group (continuous group) which is important in studying physical theories such as the Noether's theorem or local gauge transformation.
0. Since the phase angle can be infinitesimally small, this kind of group also belongs to the Lie group (continuous group) which is important in studying physical theories such as the Noether's theorem or local gauge transformation.  from a = 0, D can be expressed as:
from a = 0, D can be expressed as: 1 + i
1 + i


