
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
| Particle | Q | t | t3 | Y |
|---|---|---|---|---|
 |
0 | 1/2 | 1/2 | -1 |
| eL | -1 | 1/2 | -1/2 | -1 |
| eR | -1 | 0 | 0 | -2 |
| u | 2/3 | 1/2 | 1/2 | 1/3 |
| d | -1/3 | 1/2 | -1/2 | 1/3 |
| s | -1/3 | 0 | 0 | -2/3 |
 8/(3)1/2 generator (see Table 01 and diagrams at the top of Figure 03). The hypercharge for the hadrons, which is the composite particle with quarks, is just the sum of the individual quarks (see Table 02 and 03). The vaule of Y is related to the other quantum number in strong interaction by the formula: Y = S + B, where S is the strangeness number (0 for u and d, -1 for s), and B is the baryon number (+1/3 for quark, -1/3 for anti-quark, +1 for baryon, -1 for anti-baryon, and 0 for other particles). It was used by Gell-Mann to arrange the hadrons into geometrical patterns known as the eight-fold way (also see Figure 03). It is a plot with Y against t3. The isosinglet with one member for t = 0 is located at the center. Two isodoublets for t = 1/2 are arranged in the top and bottom row with Y = +1 and -1 respectively. The three members of the SU(3) isotriplet for t = 1 occupy the middle row, the t3 = 0 member shares the center with the isosinglet member. The particles with same isospin (same multiplet) are supposed to be similar except for the value of t3. The mass splitting among the isospin members is caused by the electromagnetic interactions as shown in Figure 04.
8/(3)1/2 generator (see Table 01 and diagrams at the top of Figure 03). The hypercharge for the hadrons, which is the composite particle with quarks, is just the sum of the individual quarks (see Table 02 and 03). The vaule of Y is related to the other quantum number in strong interaction by the formula: Y = S + B, where S is the strangeness number (0 for u and d, -1 for s), and B is the baryon number (+1/3 for quark, -1/3 for anti-quark, +1 for baryon, -1 for anti-baryon, and 0 for other particles). It was used by Gell-Mann to arrange the hadrons into geometrical patterns known as the eight-fold way (also see Figure 03). It is a plot with Y against t3. The isosinglet with one member for t = 0 is located at the center. Two isodoublets for t = 1/2 are arranged in the top and bottom row with Y = +1 and -1 respectively. The three members of the SU(3) isotriplet for t = 1 occupy the middle row, the t3 = 0 member shares the center with the isosinglet member. The particles with same isospin (same multiplet) are supposed to be similar except for the value of t3. The mass splitting among the isospin members is caused by the electromagnetic interactions as shown in Figure 04.
 |
 |
Figure 03 Eightfold Way [view large image] |
Figure 04 Mass Splitting [view large image] |
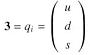 | ---------- (20) |
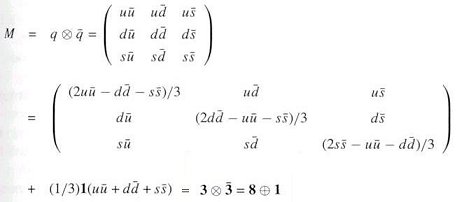 | ---------- (21) |


