Quantum Field Theory

Path Integral

In quantum theory all the paths in Figure 01c1 are possible, not just the one corresponding to

S = 0. However, not all paths are equally likely; we must find an appropriate weighting for the paths. According to Feynman, each path is weighted by the factor e^iS/. The classical path is still the one that makes S stationary under small changes of path. In its vicinity, paths have a strong tendency to add up constructively, while far from the classical path (the ones that go high up on the sides of the trough) the phase factors will tend to produce cancellations. The amount the particle can stray from the classical path depends on the magnitude of the corresponding action relative to

. The steeper the slope of the trough,

the closer it is approaching the classical theory. The classical trajectory is recovered as

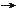0. In general, some of the paths may indicate movement at greater than light speed, or in violation of energy-momentum conservation law. Those paths would be related to the virtual particles; they need only to obey the uncertainty principle. Their contribution to the transition amplitude is usually very small. Figure 01c1 shows the different paths in 3D perspective dimensions, each one of which contributes a value to the action S (defined by Eq.(1a))

Figure 01c1 Action Principle
[view large image]

as indicated by an arrow labelled S[q(t)]. The quantum mechanical transition amplitude for going from the fixed end points q(t₁) to q(t₂) via all possible paths, is known as the Feynman Path Integral :

The sum is supposed to include all kinds of paths imaginable. However, for demonstration purpose the family of paths considered in the previous section (Figure 01a2) is sufficient. The Planck's constant can also be absorbed into the action S so that the computational procedure can be carried over to evaluate the sum. The result is presented in Figure 01c2 and 01c3 for the real and imaginary parts respectively with T =

/8.

		The blue curve shows the variation of S as a function of "a" (representing the different paths), while the red curve (not to scale) is the accumulated sum of starting from a = -50. The insert displays a much wider range for from a = -400 to a = +400. These diagrams demonstrate that the main contribution to comes mainly from paths near the classical one (around the stationary point of S). The action \|S\| assumes a pattern of rapid oscillation as its value getting larger, the amplitudes tend to cancel out each other leaving a steady value for at the asymptotic limit.
Figure 01c2 Path Integral, Real [view large image]	Figure 01c3 Path Integral, Img [view large image]

The sum can be evaluated mathematically by breaking up every path into an infinite number of intermediate points: q₁, q₂, ..., q_n, ...q_N, and then takes the sum of each point, e.g., q_n in all the paths from -

to +

(Figure 01c4). For the free field case where L = (m/2)(dq/dt)², the functional integrations can be performed analytically. After applying the Gaussian integral to all the q_n points, the final result is (see footnote for details) :

= [m/i h(t₂ - t₁)]^1/2 exp{[i m(q₂ - q₁)²] / [2

(t₂ - t₁)]} ---------- (1i)

If we vary both the end point q(t₂) and t₂, it can be shown that the transition amplitude in Eq.(1i) satisfies the time-dependent Schrodinger's equation in one dimension for a non-relativistic free particle :

Figure 01c4 Sum of Paths [view large image]

---------- (1j)

Now the transition amplitude can be equated to the wave function in the Schrodinger's equation, i.e., (x,t) = . Since when we take q(t₂) = x, t₂ = t, while q(t₁) = 0, t₁ = 0 is chosen to be the origin of the system, then Eq.(1j) can be rewritten in the more familiar form :

---------- (1k)

The link between Eqs.(1i) and (1k) illustrates the equivalence of the path integral and canonical quantization in quantum theory. Actually, the connection becomes obvious if the transition amplitude is expressed in term of a constant modulus A and phase , i.e., = Aeⁱ. For the case of free field particle = mx²/2

t = mx²/

t - mx²/2

t. If we equate the velocity v = x/t, then the energy E = mv²/2. On the other hand, the linear momentum p = mv =

k. Thus, alternatively = kx - Et/

proving that the two different expressions are exactly equivalent.

The above formulation is for the transition of the particle from one space-time point to another. The transition amplitude is called "kernel" by Richard Feynman in "Quantum Mechanics and Path Integrals" and also referred to as propagator by others. The confusion is compounded when the transition amplitude means the transition between the initial and final states of a system written as

_f(t)|

_i(t)

in the Schrodinger picture (see "Perturbation Theory and S Matrix"). One has to be really wary of what they are talking about according to the context.

Footnote for Sum of Paths :

An alternate way to perform the path integral is to sum over all the paths at different time t and then put them all together as shown in Figure 01c5, where the time coordinate is divided into N parts of equal interval

. Thus T = N

, and dt =

0. The transition amplitude , where X = q_N, can be written as :

For a particle in free field L = (m/2)(dq/dt)² it can be evaluated analytically by applying the Gaussian integral :

Figure 01c5 Path Integral
[view large image]

The integration is carried out by repeatedly applying the Gaussian integral (N-1) times :

		The real part of the transition amplitude is plotted in Figure 01c6 and 01c7 with T and X holding constant respectively. Numerical computation is performed by a home computer with Basic programming. The electron mass is assumed in the calculation with (m/h)^1/2 ~ 0.4 and (m/2) ~ 0.5. For the case of constant T, X is evaluated within the range -3 to +3 in step of 0.001 (in unit of cm); while for the case of constant X, T is evaluated from 0.5 to 5 in step of 0.0001 (in unit of sec). Fiigure 01c6 is similar to Figure 01c2; while Figure 01c7 indicates that the transition occurs preferably at T ~ 0. This is related to the relative probability P = * = (m/hT) for the particle to arrive at point X. Classically, the velocity v ~ X/T as T 0 signifies the transition to occur instantly.
Figure 01c6 X vs Transition Amplitude [view large image]	Figure 01c7 T vs Transition Amplitude [view large image]	BTW, in applying the Gaussian integral to the integration, a Wick Rotation has been performed, e.g., T -i T, the operation is reverted afterward.