
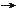 x
x + a
+ a )
)
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |

 is the Lagrangian density,
is the Lagrangian density, 
 is the
is the  th component of the field,
th component of the field,  denotes the space-time component,
denotes the space-time component,
 is an invariant function of its arguments. The form of
is an invariant function of its arguments. The form of  is further constrained by demanding that it is invariant under certain transformations such as space-time translation, Lorentz transformation, the gauge transformation, or the conformal transformation, etc.... This is to ensure that the equation of motion (field equation) is unchanged (symmetrical) under these operations. The corresponding conservation laws for these symmetries are summarized in Table 01 below.
is further constrained by demanding that it is invariant under certain transformations such as space-time translation, Lorentz transformation, the gauge transformation, or the conformal transformation, etc.... This is to ensure that the equation of motion (field equation) is unchanged (symmetrical) under these operations. The corresponding conservation laws for these symmetries are summarized in Table 01 below.| Symmetry | Group | Conservation Law |
|---|---|---|
| Space-time translation | (Translational) Poincare (x 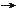 x x + a + a ) ) |
Energy-momentum |
| Space-time rotation | (Spatial) Lorentz  |
Angular momentum |
| Interal rotation of complex field | U(1) in scalar field | Total number of electric charges |
| Internal rotation of lepton or quark field | SU(2) in weak interaction | 3rd component of weak isospin |
| Internal rotation of quark field | SU(3) in strong interaction | Number of color charges |

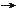
 +
+ 
 , subject to the boundary condition
, subject to the boundary condition 
 = 0 for t = t1 and t = t2, then the solution of the variational problem
= 0 for t = t1 and t = t2, then the solution of the variational problem 
 (S) = 0 yields a set of the Euler-Lagrange equations from which the equations of motion, or field equations can be derived:
(S) = 0 yields a set of the Euler-Lagrange equations from which the equations of motion, or field equations can be derived:
 | ---------- (1k) |

 | ---------- (1l) |
 , which is a function of x, y, z, and t (collectively represented by x in the equation),
, which is a function of x, y, z, and t (collectively represented by x in the equation),
