Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Quantum Field Theory

Noether's Theorem and Charge Conservation

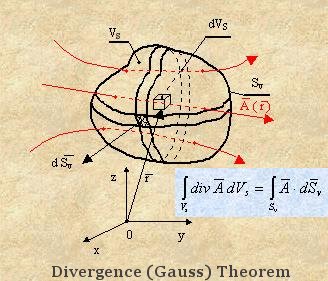Gauss Theorem The Noether's theorem in field theory takes the form of the conservation of current: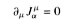


where the four-current J is defined as:
,
where is the index for the space-time, indicates the component of the field, and represents a small variation in the th parameter denoted as . From this conserved current, we can also establish a conserved

Figure 01d Gauss Theorem
[view large image]

 charge by integrating the equation over a volume in the three dimensional space. Applying the Gauss theorem (see Figure 01d), the term with spatial derivative can be converted into a surface integral, which would vanish
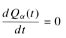if the three-current diminishes sufficiently on the surface. Under this condition, we obtain:
,
which implies the charge = constant. Note that the conservation of charge would not be valid if there is source or sink within the volume.

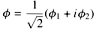The Noether's theorem can be illustrated in more details by using the two-component Klein-Gordon Equation as an example. The explicit form of the Lagrangian density in this case is:

,
where . These two independent scalar fields can be varied by the internal phase transformation:
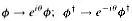or, in a more familiar form: ,
where is the parameter corresponding to ( is omitted for single parameter). This U(1) symmetry generates the four-current :. It follows that the conserved charge corresponding to this current is:

where N and N' represent the sums of number operators (in momentum space). In this form, N can be interpreted as the number of particles carrying charge -e (with various momentum), while N' is the number of anti-particles with charge +e. The sum of these numbers is a constant within a volume containing no source or sink.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.