Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Quantum Field Theory

Feynman Diagram

The first order term is:
---------- (16)
The mathematical entities inside the integral can be represented graphically by the following conventions:

which translates S(1) into a graph called the Feynman diagram:

It represents the process of the annihilation of a pair of nucleon and anti-nucleon and the creation of a pion.

In the next higher order term the normal operator will generate Green's function such as or SF(x - y) from the pairings, e.g.,

The pairing is referred to as propagator or internal line and graphically represented by a line running from a vertex at x to another vertex at y as shown in the diagram below:


which represents the annihilation of a pair of nucleon and anti-nucleon through a virtual nucleon.

Nucleons Scattering Figure 01h corresponds to the scattering of two nucleons by exchanging a pion. The internal line represents the probability amplitude for a virtual particle to travel from one place to another (x y) in a given time with greater than light speed, or to travel with off mass-shell 4-momentum k, which could have arbitrary value in violation of energy-momentum conservation but allowed by the uncertainty principle. Mathematically, it is expressed by the Green's function:

Figure 01h Nucleon-Nucleon Scattering [view large image]

where is a small positive real constant - a mathematical device taking advantage of the technique of contour integral; + 0 will be taken after the integration. The subscript F refers to the Feynman prescription for integrating the Green's functions. They are in a form such that positive energy solutions are carried forward in time, while negative energy solutions are carried backward in time. The latter solution can be interpreted as the anti-particle with positive energy moving forward in time.

Another graph such as the one below:


this loop diagram represents the process of virtual pair creation and annihilation - the vacuum fluctuation (time runs horizontally in this graph). It is this kind of graphs, which give rise to divergent results.

The Feynman rules are summarized in the tables below:

Feynman Rules Feynman Rules, Momentum Space

Table 02 Feynman Rules [view large image]

Table 03 Momentum Representations [view large image]
where in Table 02, the + and - superscripts refer to the positive frequency (eikx) and negative frequency (e-ikx) terms as shown in the Fourier decompositions below (also see Eq.(2)) . In the tables, N represents the nucleon and represents the anti-nucleon. In evaluating the S matrix, it is sometimes advantageous to go over to momentum space via the Fourier expansions:

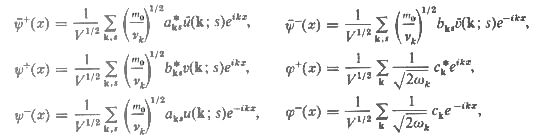
Then the Feynman rules (see Table 03) can be expressed in terms of the energy p and k = (mo2 + k2)1/2, and 4-momentum p and k, for the fermion and boson respectively, while v(p,s) and u(p,s) are Dirac spinors with spin s representing the nucleon and anti-nucleon respectively . The appearance of m0 in the formulas for both fermion and boson is rather confusing, it just indicates the rest mass for whichever particle in the process.

    As an example to demonstrate the power of Feynman diagram, the nucleon-nucleon scattering in Figure 01h will be used to evaluate the corresponding S matrix from the Feynman diagram (in momentum space, see Table 03):

  1. Collect the 4 quantum fields for the external nucleon lines (p1, 'p2, *p3, '*p4), plus other factors to be shown later.
  2. Multiply 2 coupling constants g0 and a delta function either (k - p1 + p3), or (k + p2 - p4) for the vertex x or x'.
  3. Write down a propagator F(k) for the internal line. It represents the virtual pions for all values of the 4-momentum k.
  4. Integrate over internal momenta. In explicit form :
    5. Feynman and Friends
  5. In this case of tree diagram, the delta functions enforce the rule for energy-momentum conservation such that the internal momenta k = p1 - p3 = p4 - p2. Thus, the integration can be carried out trivially. Such is not the case for a loop diagram, which diverges quadratically (see for example the self-energy diagram in Figure 03f).
  6. The integration of the k-space yields: 1/[(p1 - p3)2 - m2]
  7. The S-matrix becomes :
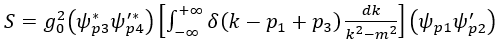
    S = (M/V)2(E1E3E'2E'4)-1/2(p1'p2*p3'*p4) {(g02)/[(p1 - p3)2 - m2]} ----- (29),
    where M and Eps are the mass and energy of the nucleons, V is the normalization volume.
  8. The scattering cross section is proportional to the squared S-matrix: |S|2.

    9. Feynman and Friends [view large image]
Evaluation of the S matrix with the Feynman rules in Table 02 yields the same result. For example, the external lines together with the contribution from the propagator would combine into a factor of exp[i(k+p3-p1)x], which gives a delta function with the same argument upon integrating over the x-space, and similarly for the y-space integration. Then the k-space integration can be performed exactly as outlined above. The rest is to collect all the factors associated with each of the steps. In fact, this is the procedure to derive the Feynman rules in momentum space.

It is worthwhile to repeat once again that Feynman diagrams can be divided into two types, "trees" and "loops", on the basis of their topology. Tree diagrams only have branches. They describe process such as scattering, which yields finite result and reproduces the classical value. Loop diagrams, as their name suggests, have closed loops in them such as the one for vacuum fluctuation. The loop diagrams involve "off mass-shell" virtual particles and is usually divergent (becomes infinity). Such virtual particles can appear and disappear violating the rules of energy and momentum conservation as long as the uncertainty principle is satisfied. They are said to be "off mass-shell", because they do not satisfy the relationship E2 = p2c2 + m2c4.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.