Quantum Field Theory

Yang-Mills Theory

The Yang-Mills (Figure 03i) theory was originally devised to discribe the strong interaction between nucleons (neutrons and protons, now recognize as not elementary) mediating by gauge bosons - the pion in this case. It was also involved in the early attempt to formulate a

		gauge theory for the weak interaction. It is a generalization of the U(1) gauge theory for QED with non-abelian group (for the internal space). It fails to account for the mass of the gauge bosons in the interaction. However, it provides a good framework for QCD in strong interaction as its mediating bosons are massless. Since non-abelian gauge bosons can be emitted and absorbed from the gauge bosons themselves (see Figure 03j), they create anti-shielding for the quark anti-quark pairs in the virtual particle cloud (the Yukawa cloud). The color charge becomes weaker at smaller probing distance, and leads to asymptotic freedom. Conversely, at larger distances, the color charge increases,
Figure 03i Yang-Mills [view large image]	Figure 03j Gluon Vertex	so that the quarks tends to bind more tightly together giving rise to quark confinement, which is the flip side of asymptotic freedom.

The mathematical formulation starts with the local gauge transformation of the fermion field:

' = exp(i

(x)

)

where

(x) is a function of x denoting the phase angles in the internal space, and

represents three 2x2 non-commuting matrices (generators) for the SU(2) group; and eight 3x3 non-commuting matrices for the SU(3) group. In other word, this kind of transformation is non-abelian.

The problem with the construction is that the derivatives of the fermion field are not covariant under this transformation. It can be shown that the formulation is invariant only if the derivative is replaced by the covariant derivative:

D = + i

^ab^a

where the space-time component is labeled by the index

, the index "a" is for the phase angles,

is the coupling constant, and

b =

^ab^a represents the new fields (the gauge bosons) introduced to render an invariant theory under the local gauge transformation. Then the Lagrangian density takes the form:

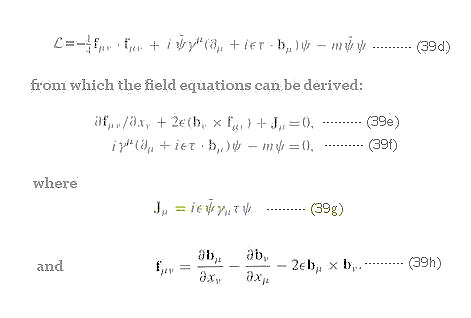
The field equation for the fermion in Eq.(39f) appears to be similar in form to the one for QED (see Eq.(13)) with the interaction Hamiltonian in Eq.(38b), except that the abelian gauge boson field A is now replaced by the non-abelian gauge boson fields
^ab^a.

The field equation for the gauge boson in Eqs.(39e) and the definition of f in Eq.(39h) is similar to the electromagnetic field equation in Eqs.(23) and (24), except an additional non-linear term, indicating that the b's interact among themselves (with the same coupling constant, also see Figure 03j) and is responsible for the anti-shielding effect.

While the f in Eq.(39d) can be identified to W in Eqs.(41a) and (42a) for the Standard Model. The Yang-Mills theory fails to account for the chiral nature of the fermion fields in weak interaction. Parity violation in weak interaction has not been discovered until 1957 - four years later than the introduction of the Yang-Mills theory.

The mass for the vector bosons in weak interaction is absent in the Yang-Mills theory. Only the fermion mass is hand written into the formulation. The Standard Model takes care of both via the interaction with the Higgs field in Eq.(41c). The problem with the gauge-field mass is recalled fondly in an anecdote by C. N. Yang (1922-).

The Lagrangian density Eq.(39d) in the Yang-Mills theory is virtually identical to the QCD's in Eq.(43), except that the number of fermions (quarks) is six altogether. Such data were not available to Yang and Mills in 1953.

For convenience, most of the formulas in quantum field theory are expressed in natural units with = 1, c =1, then becomes dimensionless. Otherwise, the mass term in the formulism would be m/c; while the interaction term would appear as (/c)b.

The Yang-Mills theory is applicable to the early universe when the temperature was higher than 250 Gev (see table on "A History of Cosmic Expansion"). The Higgs field, which endows mass to most of the elementary particles, was still in its symmetrical state, and was unable to interact with them. Thus, all particles are massless and the Yang-Mills theory is perfectly suitable to describe them.

The Yang-Mills theory has been used as toy model to study supersymmetry. Its Euclidean space-time version is the base for the notion of instanton.

Quantum Field Theory

Yang-Mills Theory

Figure 03i Yang-Mills [view large image]

Figure 03j Gluon Vertex

Go to Next Section or to Top of Page to Select or to Main Menu

Go to Next Section
or to Top of Page to Select
or to Main Menu