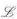 :
:
 and
and  are indices for the space-time components running from 1 to 4. Whenever an index appears in both the subscript and superscript, it signifies a summation over these components.
are indices for the space-time components running from 1 to 4. Whenever an index appears in both the subscript and superscript, it signifies a summation over these components. is related to the three gauge (vector) bosons with the index "a" running from 1 to 3.
is related to the three gauge (vector) bosons with the index "a" running from 1 to 3.
 is the anti-symmetric tensor for the electromagnetic field as shown in Eq.(24), where the vector potential A
is the anti-symmetric tensor for the electromagnetic field as shown in Eq.(24), where the vector potential A is now denoted by B
is now denoted by B .
.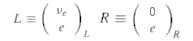 | ---------- (42f) |
 .
. are the Pauli matrices as shown in Eq.(10) in the appendix on "Groups" with i running from 1 to 3. The four 4X4 gamma metrices
are the Pauli matrices as shown in Eq.(10) in the appendix on "Groups" with i running from 1 to 3. The four 4X4 gamma metrices  are constructed from the Pauli matrices and the identity matrix,
are constructed from the Pauli matrices and the identity matrix, 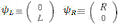 , and
, and  is the adjoint spinor of
is the adjoint spinor of  where
where 
 is the Hermitean conjugate ,
is the Hermitean conjugate ,  .
.
 and B
and B boson respectively. Ge is the Yukawa coupling constant, which defines the strength of the interaction between the Higgs field and the lepton fields.
boson respectively. Ge is the Yukawa coupling constant, which defines the strength of the interaction between the Higgs field and the lepton fields. is the Higgs doublet with four real components, three of which will be absorbed by the W
is the Higgs doublet with four real components, three of which will be absorbed by the W , and Z0 to become massive. The diagram below shows a simplified Higgs field in the shape of a Mexican hat:
, and Z0 to become massive. The diagram below shows a simplified Higgs field in the shape of a Mexican hat: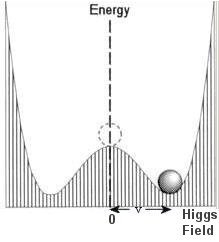
This form of field exhibits a drastic effect called "spontaneous symmetry breaking". When the origin of the field is shifted to v =
 (-2m2/
(-2m2/ )1/2 (the scalar field at minimum energy) by the transformation
)1/2 (the scalar field at minimum energy) by the transformation  ' =
' =  - v, the fields Wa
- v, the fields Wa and B
and B recombine and reemerge as the physical photon field A
recombine and reemerge as the physical photon field A , a neutral massive vector particle Z
, a neutral massive vector particle Z , and a charged doubled of massive vector particles W
, and a charged doubled of massive vector particles W
 . In terms of the Weinberg angle (mixing angle) tan
. In terms of the Weinberg angle (mixing angle) tan = g'/g,
= g'/g,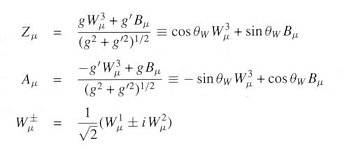
Thus, the transformation from (B
 , W
, W 3) to (A
3) to (A , Z
, Z ) can be considered as a rotation of the mixing angle.
) can be considered as a rotation of the mixing angle.The masses of the gauge bosons are obtained from the formula:

where we have used the known constants for GF = 1 / v221/2 = 1.14x10-5 Gev-2, e = g sin
 W = (4
W = (4
 )1/2 = 0.3028, and from the measurement of sin2
)1/2 = 0.3028, and from the measurement of sin2 W = 0.226
W = 0.226  0.004 to evalutate the masses for the gauge bosons. The theoretical values are in good agreement with MW = 80.4 Gev, and MZ = 91.19 Gev determined by experiments.
0.004 to evalutate the masses for the gauge bosons. The theoretical values are in good agreement with MW = 80.4 Gev, and MZ = 91.19 Gev determined by experiments.


 =
=  .
.


 represents the
represents the  b baryons. The bottom quark within these baryons can turn into an up quark during the process. It is from such observations that the weak interaction involves only
b baryons. The bottom quark within these baryons can turn into an up quark during the process. It is from such observations that the weak interaction involves only 

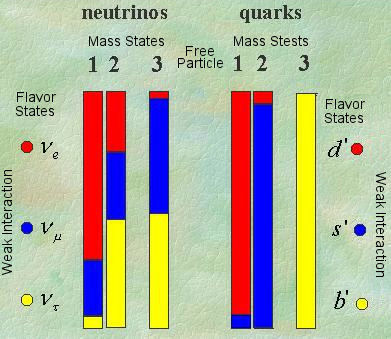
 tunrs some matrix elements into
tunrs some matrix elements into  )
and the mass (mixed) states (
)
and the mass (mixed) states (

 . Quantum Fields form the physical foundation of the Standard Model (SM) of particle physics. The Standard Model is fundamentally a quantum field theory (QFT), specifically a combination of quantum mechanics and special relativity, where the entities of interest are fields rather than particles.
. Quantum Fields form the physical foundation of the Standard Model (SM) of particle physics. The Standard Model is fundamentally a quantum field theory (QFT), specifically a combination of quantum mechanics and special relativity, where the entities of interest are fields rather than particles.
 Changing the gauge does not change the position of the ship (the field in QFT).
Changing the gauge does not change the position of the ship (the field in QFT). .
Pictorial Examples for Specific fields :
.
Pictorial Examples for Specific fields :