| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
This idea can be applied to the theory of cosmic inflation or to account for the mass of elementary particles in the Standard model via interaction with the Higgs boson as shown below. Let us start by examine how such unstable symmetry can arise mathematically. Considering the Lagrangian for a scalar field with the potential V: L = (1/2)       - V( - V( ) ---------- (46) ) ---------- (46)where V(  ) = (1/2)m2 ) = (1/2)m2 2 + ( 2 + ( /4!) /4!) 4, and 4! = 4x3x2x1. 4, and 4! = 4x3x2x1.
|
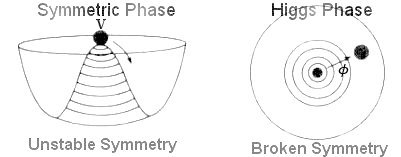
Figure 06f Scalar Field |
If m2 > 0, the system has real mass, the potential exhibits a minimum at the origin, where  = 0. This system is associated with a unique vacuum = 0. This system is associated with a unique vacuum  (see Figure 06f). (see Figure 06f). |
 = 0 is unstable; a particle would prefer to move down the potential to a lower-energy state at the bottom of one of the wells at
= 0 is unstable; a particle would prefer to move down the potential to a lower-energy state at the bottom of one of the wells at  = v =
= v =  (-6m2/
(-6m2/ )1/2. The states at
)1/2. The states at  = 0, and
= 0, and  = v are referred to as false vacuum, and true vacuum respectively (Fiigure 06f). Eq.(46) indicates that the system is symmetrical under
= v are referred to as false vacuum, and true vacuum respectively (Fiigure 06f). Eq.(46) indicates that the system is symmetrical under 
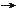 -
- . If the origin at the false vacuum is shifted to v, i.e.,
. If the origin at the false vacuum is shifted to v, i.e.,  ' =
' =  - v, then the Lagrangian in Eq.(46) becomes:
- v, then the Lagrangian in Eq.(46) becomes:

 '
'

 ' - V'(
' - V'( ') ---------- (47)
') ---------- (47) ') = |m|2
') = |m|2 '2 + (1/6)
'2 + (1/6) v
v '3 + (
'3 + ( /4!)
/4!) '4. In this way, the scalar particle has acquired a positive mass squared given by 2|m|2, but the original symmetry between
'4. In this way, the scalar particle has acquired a positive mass squared given by 2|m|2, but the original symmetry between  and -
and - has been spontaneously broken because the field has been shifted (resulting in the occurrence of the
has been spontaneously broken because the field has been shifted (resulting in the occurrence of the  '3 term) and there is a true vacuum at
'3 term) and there is a true vacuum at  ' = 0. Note that the valley in diagram (b) has a depth of (3/2)(m4/
' = 0. Note that the valley in diagram (b) has a depth of (3/2)(m4/ ). The zero point of the potential can be shifted up or down without any effect on subsequent calculation.
). The zero point of the potential can be shifted up or down without any effect on subsequent calculation. |
The formulation can be generalized to complex scalar field with two independent components corresponding to positively and negatively charged fields. In a slightly different notations, the Lagrangian for a complex scalar field has the form similar to Eq.(46): L = (    )( )(   *) - V( *) - V( , , *) ---------- (48) *) ---------- (48)where V(  ) = m2 ) = m2  * + ( * + ( /4)( /4)(  *)2. *)2.
|
Figure 06g Complex Scalar Field [view large image] |
 )2 + (Im
)2 + (Im )2 = v2, where v = (-2m2/
)2 = v2, where v = (-2m2/ )1/2 (see Figure 06g). Therefore, there are infinitely many possibilities for the stable configuration: any scalar field
)1/2 (see Figure 06g). Therefore, there are infinitely many possibilities for the stable configuration: any scalar field  satisfying the condition for minimum energy will do. The Lagrangian in Eq.(48) is invariant under the global gauge transformation:
satisfying the condition for minimum energy will do. The Lagrangian in Eq.(48) is invariant under the global gauge transformation: = (
= ( 1 + i
1 + i 2)ei
2)ei /(2)1/2
/(2)1/2 1-
1- 2 plane. In analogy to the previous example, the origin of one of the field components, e.g.,
2 plane. In analogy to the previous example, the origin of one of the field components, e.g.,  1 is shifted to a point at the circle of minimum energy:
1 is shifted to a point at the circle of minimum energy: =
=  1 - v
1 - v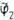 =
=  2
2 , and
, and 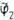 , the Lagrangian is transformed to:
, the Lagrangian is transformed to: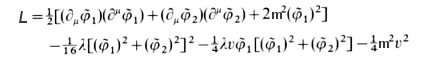
 acquires a (positive) mass squared of -2m2. The novel feature in this example is that the field
acquires a (positive) mass squared of -2m2. The novel feature in this example is that the field 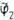 remains massless. Such massless modes, which arise from the degeneracy of the ground state after spontaneous symmetry breaking, are called "Goldstone bosons". The appearance of Goldstone bosons seems to be in contrary to real world experience since no such massless, spin-0 particle exists.
remains massless. Such massless modes, which arise from the degeneracy of the ground state after spontaneous symmetry breaking, are called "Goldstone bosons". The appearance of Goldstone bosons seems to be in contrary to real world experience since no such massless, spin-0 particle exists. and electromagnetic vector potential A
and electromagnetic vector potential A has the form:
has the form:

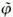 ' = e-iq
' = e-iq
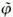 , with q
, with q = tan-1(
= tan-1(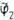 /
/ )
) ' = H =
' = H =  cos(q
cos(q ) + i
) + i 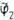 sin(q
sin(q )
)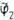 ' = 0
' = 0
 , which has acquired a mass qv. The remaining scalar field H has also acquired a mass (-2m2)1/2. The total number (four) of degrees of freedom is unaltered. Instead of a massless gauge boson, having two (transverse) modes, plus a complex field
, which has acquired a mass qv. The remaining scalar field H has also acquired a mass (-2m2)1/2. The total number (four) of degrees of freedom is unaltered. Instead of a massless gauge boson, having two (transverse) modes, plus a complex field  composed of two real components, we now have a massive vector field A'
composed of two real components, we now have a massive vector field A' having three modes - two transverse and one longitudinal (a requirement for massive spin-1 boson), plus one real scalar field H. This is just a theoretical model to illustrate the effect of spontaneous symmetry breaking. Of course, the photon remains massless in the real world. It requires both spontaneous symmetry breaking (with v
having three modes - two transverse and one longitudinal (a requirement for massive spin-1 boson), plus one real scalar field H. This is just a theoretical model to illustrate the effect of spontaneous symmetry breaking. Of course, the photon remains massless in the real world. It requires both spontaneous symmetry breaking (with v 0) and the coupling of the gauge field to the scalar field (q
0) and the coupling of the gauge field to the scalar field (q 0) to acquire a mass. A more complicated version of this model is applicable to the electroweak interaction in the Standard model. It has been shown subsequently by 't Hooft that the spontaneous symmetry breaking formulation remains renormalizable; the ultraviolet divergences encountered are no worse than those occurring in QED.
0) to acquire a mass. A more complicated version of this model is applicable to the electroweak interaction in the Standard model. It has been shown subsequently by 't Hooft that the spontaneous symmetry breaking formulation remains renormalizable; the ultraviolet divergences encountered are no worse than those occurring in QED. |
As each term in the Lagrangian of the Standard model represents a different process, Figure 06h shows the various Higgs interactions in the form of Feynman diagrams. Diagram (a) represents a fermion emitting or absorbing a Higgs particle. Diagram (b) shows the corresponding process for the gauge bosons. They can also interact simultaneously with two Higgs, as shown in (c), which also represents a gauge boson scattering a Higgs particle. The Higgs also interacts with itself, as shown in diagrams (d) and (e), which are related to the shape of the scalar potential (Figure 06g). Diagram (f) depicts an electron acquiring its mass. |
Figure 06h Higgs Field Interaction |
 |
By taking into account the higher term of the SM (Standard Model) perturbation series, the vacuum potential of the Higgs field V is in the form :
 |
Figure 06i Stability of the Universe [view large image] |
and the sum is over all SM particles acquiring a Higgs-dependent mass Mi. The precise form of V1 is not important in the present context, it just shows that the Higgs potential also depends on the particles it acts upon. Furthermore, only the heaviest top quark in the sum is retained in the following consideration. |