Relativity, Cosmology, and Time

Special Relativity

The search was on in the late 19th Century for the elusive ether. Finally in 1887 Michelson and Morley demonstrated conclusively that the speed of light in different inertial frames is the same everywhere (Figure 02b). The Maxwell's equations for electromagnetic wave also indicates that the speed of light is a constant regardless of the relative motion of the person measuring that speed. But as just mentioned above, the velocity of light is different in different inertial frame according to the Galilean transformation. The theory of special relativity was postulated to reconcile this kind of inconsistency. The theory does away with the idea of absolute frame of reference such as the ether, and treats all inertial frames on an equal footing.

Figure 02b Michelson-Morley Experiment [view large image]

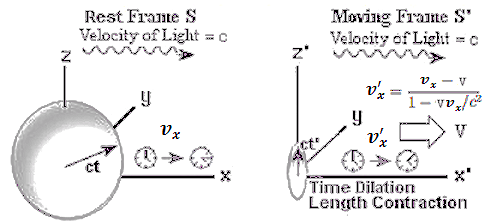Mathematically if a spherical light wave is generated at the origin of the S and S' inertial frames when they are coincided at t = 0, the statement about the constant velocity of light in different inertial frames can be expressed as: x2 + y2 + z2 = c2 t2   or   x2 + y2 + z2 - c2 t2 = 0    (for an observer in the S frame) ---------- (6) x'2 + y'2 + z'2 = c2 t'2   or   x'2 + y'2 + z'2 - c2 t'2 = 0     (for an observer in the S' frame) ---------- (7)

Figure 02c Constant Speed of Light [view large image]

• The independent time variable t is now treated almost on the same footing as the other spatial dimensions except carrying a negative sign earning "ct" the designation as pseudo-coordinate (Eqs.6, and 7).




The length L' = x'2 - x'1 at t'2 = t'1 in the moving inertial frame is now different to the length L with respect to an observer in the S system. According to the first formula in Eq.(8b), the relation is given by : L = x2 - x1 = L' / (1 - V2/c2)1/2 or L' = L (1 - V2/c2)1/2, which is known as the Lorentz contraction. The length of a moving rod is shorter according to an observer in the S' frame. The phenomena is demonstrated in high energy collision, when the round shape of atom becomes a pancake with the flatten face perpendicular to the direction of motion (Figure 03).

Figure 03 Lorentz Contraction from S' Frame [view large image]



• The time interval T' = t'₂ - t'₁ of a clock sitting in the S' system appears to take longer to tick with respect to a stationary observer in the S system. According to the 4^th formula in Eq.(8b), the time intervals is given by T = T' / (1 - V²/c²)^1/2 or T' = T (1 - V²/c²)^1/2 for a clock sitting at x', i.e., this clock appears to run slower according to an observer in the S system (Figure 02c). The effect is known as time dilation and T' is referred to as the proper time - the time read by a clock moving together with the frame. The phenomenon is demonstrated in the decay of unstable particle moving at near the speed of light. The lifetime of such particle appears to be much longer than the one measured in a stationary lab. The diagrams in Figure 04a show the muon decay as experienced in its own frame and from the view point of a stationary observer on Earth.

  		The twin paradox is another consequence of time dilation. As shown in Figure 04b, one of the twin (at O) leaves on a space journey during which he travels close to the speed of light, while his sister remains on Earth. Because of his motion, time runs more slowly in the spacecraft as seen by the earthbound twin. So on his return the space traveler (at B) will find that his sister has aged more than himself as indicated by the clock readings in line OB (for the sister) and OAB (for the brother). The paradox arises because it can be argued that the sister is moving near the speed of light relative to her brother and so the brother should be getting older instead. A number of experiments have confirmed that the traveling twin would indeed be younger. The two world-lines are different, and not interchangeable; the traveling twin's frame is not an inertia one at the turning point.
  Figure 04a Dilation in S Frame	Figure 04b Twin Paradox

  For an infinitesimal interval of space-time, Eq.(6) can be written in the form: c2 dt2 - dx2 - dy2 -dz2 = 0 ---------- (9) This is called the null line for object moving at the speed of light. In place of the invariant lenght d in Eq.(5) under the Galilean Transformation, for object moving with velocity not equal to the speed of light, the space-time interval "ds" (aka the "world line" - the path of a particle in 4-D space-time) is : ds2 = c2 dt2 - dx2 - dy2 - dz2 ---------- (10) which is invariant under the Lorentz transformation. For a clock at rest in a reference frame, that is, with dx = dy = dz = 0, d = ds/c is called the proper time.

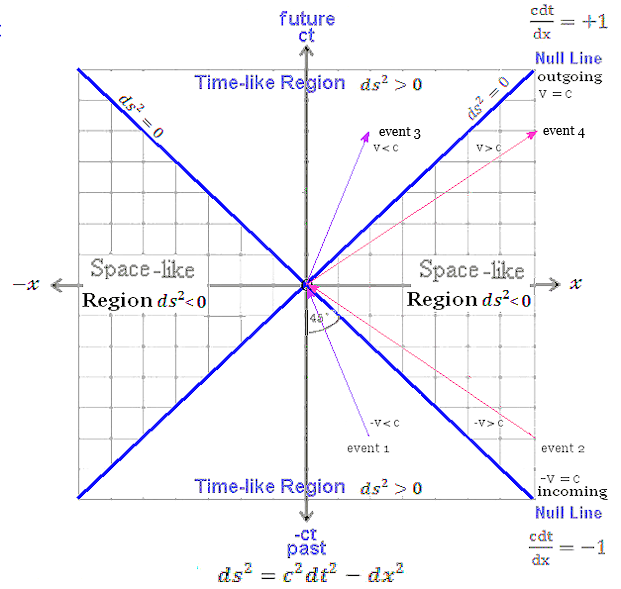
  Figure 04c Minkowski Space-time [view large image]

  In general, by denoting v2 = [(dx/dt)2 + (dy/dt)2 + (dz/dt)2], Eq.(10) can be re-written as : ds2 = (1-v2/c2)c2dt2.

  The interval is called time-like if ds2 0. As shown in figure 04c, event 1 can be related causally to an observer at the origin x = 0, ct = 0 (the "now") from the past with incoming velocity v c. If ds2 < 0, it is called space-like, which implies event 2 is entirely unrelated to that observer, since it would require a flow of information at speed faster than the speed of light. Similarly, time-like separation can influence a receiver in the future, while outgoing communication is impossible with space-like linkage. The space-time interval ds (or proper time d) plays the role of the time parameter in Newtonian mechanics to keep track of the development of events as shown in the generalized equation of motion in Eq.(12b). Note that the velocity of light c is constant in all Lorentz frame of references in Figure 05 as originally envisioned.

  Figure 05 Minkowski Space-time Transformation [view large image]

  BTW, an event is a point in the four dimension space-time.

  Events take place simultaneously to an observer in S, e.g., t = to at x = x1 and x = x2, are separated by a time interval in S' according to the 4th formula in Eq.(8a) (see Figures 05) : t'2 - t'1 = [(x1 - x2)(V/c2)] / (1 - V2/c2)1/2 Figure 05a shows the different perspective according to the stationary observer C, who sees simultaneity of two lightnings, while D in the moving bus detects the lightnings in different time.

  Figure 05a Simultaneity [view large image]

  Specifically in the moving bus, the signal from A takes longer time t'1 to reach D than t'2 from B.

  
  
• Closer examination reveals that Eq.(10) is not a sum of squares of the coordinate differentials. One of these is associated with an opposite sign. This is called pseudo-Euclidean geometry and is the reason for the un-usual appearance of the space-time axes when subject to a rotation in the Minkowski space-time as shown in Figure 05 (don't ever try to visualize the geometric configurations in such pseudo-Euclidean space - it will drive you crazy). Mathematically, the Minkowski space-time rotation can be expressed in a form resembling to the 2-dimensional rotation by re-writing Eq.(8b) in term of the hyperbolic functions:
  
  x = x' cosh(A) + c t' sinh(A)
  ct = x' sinh(A) + c t' cosh(A)
  
  where tanh(A) = (V/c), sinh(A) = (V/c) , cosh(A) = are the hyperbolic functions, and = 1 / (1 - V² / c²)^1/2. As V approaches c, tanh(A) ~ 1, the x' and ct' axes merge together at the null line (see Figure 05).


• In Galilean transformation, the velocity with respect to the S' system is v'_x = v_x -V, which is now replaced by
  v'_x = (v_x - V) / (1 - v_xV/c²) in special relativity (see Figure 02c). Incidentally, this formula yields correctly v'_x -c as V c.


• Using the space-time interval ds as the parameter independent of different inertial frames (in particular d = ds/c with dx = dy =dz = 0, i.e., in the rest frame is called the proper time), the velocity in the 4 dimensional space-time can be defined as:
  u_k = dx_k/d = v_k,
  u₀ = ic(dt/d) = ic,
  where the index k runs from 1 to 3 for the x, y, z dimensions and ct is denoted as the 0th or the rather misleading ID as the 4th dimension.
  By definition the square of the 4-velocity u² = (u₀)² + (u_k)² = -c² is invariant under the Lorentz transformation.


• Similarly the 4-momentum is defined as:
  p_k = m_ov_k,
  and p₀ = im_oc.
  The square of the 4-momentum p² = (p₀)² + (p_k)² = -m_o²c² is another 4-scalar quantity invariant under the Lorentz transformation.
  The 4th component is linked to the total energy E by the formula: p₀ = iE/c, thus
  E = m_oc² = mc²
  where m = m_o. The relationship is justified by the correct limit at low speed when E m_oc² + m_ov²/2. This is the origin of the most celebrated formula derived by Einstein. For particle with no mass m₀ = 0, it has to move with the velocity of light, i.e., v = c to render a finite energy E.


• Thus, the mass for a particle moving at velocity v is given by m = m_o / (1 - v²/c²)^1/2, where m_o is the rest mass (relative to the observer's rest frame). This formula shows that m as v c. It means that objects with mass can never be accelerated to the speed of light or greater.


• It also shows that mass and energy are equivalent. They can be converted to each other. The total energy E of a particle is given by the formula E = m c² or E = m_o c² + T. The first term is the rest mass energy, and the second term is the kinetic energy (at speed up to c)
  T = [1/(1 - v²/c²)^1/2 -1] m_oc².



In term of the 3-momentum p, E = (mo2 c4 + p2 c2)1/2 from which the relationship between v and p can be derived in the form : (v/c)2 = 1/[1 + (moc/p)2]    or    p2 = mo2c2{(v/c)2/[1 - (v/c)2]} For mo2 > 0, the particle is always moving slower than the velocity of light. For mo2 = 0, v is always equal to c. If mo2 < 0 then v > c, i.e., the particle is moving faster than the velocity of light. Such particle is called tachyon, which has the peculiar property that it slows down to approach the velocity of light with increasing momentum p, while its speed goes up to infinity as p falls to |mo|c (see Figure 06a).

Figure 06a Mass and Velocity [view large image]

There is no direct evidence that tachyons exist, and most physicists believe there is something wrong or it requires some sort of interpretation when they appear in a theory. The spontaneous symmetry breaking potential in the Higgs mechanism is one example of tachyon in physics.

Note that the Higgs particle is not tachyonic, it acquires real mass after symmetry breaking from the unstable configuration. Another example is the quantized bonsonic string, which admits tachyonic state. It is eliminated after introducing super-symmetry into the theory.


• Table 01 illustrates the differences between timelike and spacelike objects, where x and p denote the 3-D spacetime vector and 3-D momentum respectively, and v = | dx/dt |. In quantum field theory, the virtual particles possess spacelike or off mass-shell characteristics, which enable physicists to resolve a variety of problems. Off mass-shell means that the relation m_o²c² = E²/c² - p² is no longer valid. For a real photon ds = 0, and m_o = 0, otherwise it is an off mass-shell virtual photon.
  
  

  Mathematical Entity	Timelike	Spacelike	Spacelike Property
  4-D Spacetime Vector	x = (ct, x)	x = (ct, x)	Outside light cone
  Spacetime Interval	ds2 = c2dt2 - dx2 0	ds2 = c2dt2 - dx2 < 0	v > c - tachyon
  4-Momentum	p = (E/c, p)	p = (E/c, p)	Outside light cone
  4-Momentum Squared	mo2c2 = p2 = E2/c2 - p2 0	mo2c2 = p2 = E2/c2 - p2 < 0	Off mass-shell - tachyon
  4-Momentum Transfer	p' - p = [(E' - E)/c, (p' - p)] = q	p' - p = [(E' - E)/c, (p' - p)] = q	Outside light cone
  4-Momentum Transfer Squared	(p' - p)2 = (E' - E)2/c2 - (p' - p)2 = q2 0	(p' - p)2 = (E' - E)2/c2 - (p' - p)2 = q2 < 0	Off mass-shell

  Table 01 Spacelike Characteristics

  A general rule for space-like quantity is for those 4-scalar such as ds, m_o, or q to become a complex number.


• In special relativity the equation of motion for a particle is:
  
  f_k = m_o(du_k/d)
  
  where the space component of the velocity is u = v/(1-v²/c²)^1/2, the time component is u₀ = c /(1-v²/c²)^1/2, while the space components of the four vector f_i form a vector f / (1-v²/c²)^1/2 where f = m₀(dv/dt), the time component is f₀ = f(v/c) / (1-v²/c²)^1/2 (since f_ku_k = 0). This equation is invariant under the Lorentz transformation. In general, all laws of physics are required to be invariant under the Lorentz transformation. It means that all physical laws are prescribed to retain the same form in all inertial frames of reference (as these frames are only artificial objects). This is the "principle of general covariance" originally envisioned by Einstein for special relativity. It has since then been generalized to encompass many different kinds of transformation such as the coordinate transformation and gauge transformation, ... etc.



• Historically, when deriving the formulas of relativistic transformation, Poincare, Einstein and Lorentz originally proposed a more general form with a scale factor as shown in Eq.(11a), but all three came to the conclusion later that it should be equated to 1, i.e. the multiplier was excluded from the formulas. However, there is a modern work (see "Memoir on the Theory of Relativity and Unified Field Theory") where it is argued that this conclusion was wrong, and that the physical meaning of the scale multiplier is to reflect the Doppler effect. In this case, the scale factor is in a form given by Eq.(11c).
  
  x' = (V)(V)(x - Vt),    y' = (V)y,    z' = (V)z,    t' = (V)(V)(t - Vx/c²) ---------- (11a),
  where (V) = (1 - V²/c²)^-1/2 ---------- (11b),
  (V) = [(1 + V/c)/(1 - V/c)]^1/2 ---------- (11c),
  thus, (V)(V) = 1/(1 - V/c) ---------- (11d).
  
  They transform the space-time interval (relative to the origins) as x'² + y'² + z'² - c²t'² = ²(V) (x² + y² + z² - c²t²) ---------- (11e).
  
  
  Here's some comments (see a pictorial displays for the 2 different versions in Figure 06b) :
  
  
  • The Einstein's version (Figure 06b,a) asserts that the velocity of light is a constant c = 3x10¹⁰ cm/sec regardless of the motion of the inertial frame. For an observer in a stationary frame O, light takes a time interval t = OB/c to arrive at B; light from a moving frame O' would arrive the same time at B if they both flashed at the same instant and same location.
  
  
  • The original version (Figure 06b,b) takes into account the Doppler shift with an additional multiplier (V) as shown in Eqs.(11a,b,c,d). The velocity of light is c + V, it is no longer independent of the relative motion of the inertial frames. Einstein's version is a special case for (V) = 1.
  
  
  • Beside taking into consideration the Doppler effect, the original version also change the scale of the space-time interval as shown in Eq.(11e). It is structured to compensate the velocity dependence so that both signals from O and O' would arrive point B at the same time. Such formulation is called scale invariance.
  
  
  • The problem with the original version is related to the addition of Doppler effect. In such formulation, the factor for the dilation of clock, and the shortening of length becomes (1 - V/c) in the moving frame instead of (1 - V²/c²)^1/2. As a result, the moving clock could tick faster, the length could appears to be longer when the velocity V is negative (in the approaching scenario with V = -|V|), and there is no evidences for such phenomena.
  
  

  	The mass in the moving frame would decrease according to m = m0/(1 - V/c) if V is negative; it is also contrary to experiment. All such discrepancies are attributed to inaccurate measurements or mis-interpretations by proponents of the original version. It is claimed that the original version resolves the Twin Paradox naturally, because
  Figure 06b Special Theory of Relativity - 2 Versions [view large image]	Age-of-Travelling-Twin = T'(outbound) + T'(inbound) = T(1 - |V|/c) + T(1 + |V|/c) = 2T = Age-of-Earth-bound-Twin (see "Twin Paradox").

Go to Next Section
 or to Top of Page to Select
 or to Main Menu