Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Relativity, Cosmology, and Time

General Relativity

Free-falling Frame Equivalence The inertial frames of reference in both classical mechanics and special relativity move with a constant velocity related to each others. Such arrangement seems to become impossible in the presence of gravity, which produces acceleration (change of velocity). However, there is a class of inertial frames of reference that can be obtained locally by letting it freely falling. This kind of frames would generate an opposite force, which exactly nullifies the acting force. The local region (such as in an elevator) would experience zero gravity as shown in Figure 07a. Figure 07b shows the similar kind of situation in producing gravity with acceleration.

Figure 07a Free-falling Frame

Figure 07b Equivalence Principle
[view large image]

 The inter-changeable nature of gravity and acceleration (at least locally) is known as the principle of equivalence.

Drop Tower, Old and New As shown in Figure 07b, the principle of equivalence is valid only when the gravitational mass mg is equal to the inertial mass ma. The latest challenge to the theory of General Relativity is about the equality of these quantities. It is suggested that new physics would emerge if they turn out to be un-equal. A modern version of the "leaning tower" experiment (Figure 07c, the one on the left was used by Galileo in 1589) inaugurated in 1990 provides free fall environment up to 9.3 seconds, from which various kinds of atoms have been found to fall at the same rate to accuracies of 11 decimal places. A 2016 project leaded by the French will carry out further measurements in the micro-gravity condition of space to achieve accuracy 100 times better than those from laboratories on Earth.

Figure 07c Drop Towers, Old and New [view large image]

 The drop tower experiment assumes mg = ma, which implies that all objects accelerate at the constant rate of g = 9.8 m/sec2 if the principle of equivalence is valid.

Anyway, according to Einstien, the space-time interval in Eq.(10) is still valid for the observer confined to the free-falling frame of reference (inside the elevator), where no external force is perceived. However, since the gravitational field is in general not uniform, the global space-time interval outside the local frame is expressed by the more general formula:

ds2 = gik dxi dxk ---------- (11)

where the notations have been simplified such that x = x1, y = x2, z = x3, ct = x4; the indices i, k run from 1 to 4 and the repeated dummy index in the equation is understood to be summed over the 4 space-time coordinates. The gik is known as
Worldline space-time metric tensor, which is a second rank tensor and a function of the space-time. For the inertial or free-falling frame (flat space-time), g11 = g22 = g33 = -1, g44 = 1, and gik = 0 for i k. Eq.(11) can be alternatively viewed as the space-time interval of a curved world-line (Figure 07d) as opposed to a straight world-line for the free field case.

Figure 07d Null Cones in Flat and Curved Spacetime

Figure 07d shows the difference between the flat and curved spaces in terms of the light (null) cones. In the Minkowskian flat space, all the null cones align identically with the boundary at 45o for the propagation of photon, all the massive particles is confined within
the cone - a vertical straight line represents a particle a rest, other straight lines for moving with constant velocity, and the curved line for accelerating/decelerating motion. In the Lorentzian curved space, the cones oriented in different directions according to the curvature. At the event horizon of a black hole, the cone would shrink 45o so that no photon or any kind of objects can escape to outside (see Figure 09f). The principle of equilibrium can be portrayed as the small segment of a curvilinear path that is pointing at the time direction by selecting a suitable frame of reference, e.g., the freely falling frame, at a particular space-time point such as "p" in diagram b. In general this special status will disappear a short while later.

Mathematically the space-time metric gik is determined by the nonlinear differential equations (see "Differential Equation" for a very brief introduction) as postulated by Einstein:

Rik = (8G/c4) (Tik - gikT/2) ---------- (12a)
where 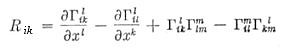is a second rank tensor (Ricci Tensor) related to the curvature of space-time,
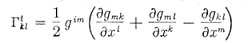is the Christoffel symbol, and Tik is the energy-momentum tensor (Figure 07e), T its trace.
Thus, gravity is geometrized and the geometry of the space-time is ultimately determined by matter-energy. Eq.(12a) is invariant under general coordinate transformations to satisfy the requirement that physics should not change by the re-assignment of coordinates.

Energy-Momentum Tensor

Figure 07e Energy-Momentum Tensor [view large image]

See more details for "Scalar Curvature".

The equation of motion for a particle in relativity is the geodesic (shortest path) in 4-dimensional space-time:

d2xi/ds2 + ikl (dxk/ds) (dxl/ds) = 0 ---------- (12d)

Since ui = dxi/ds is the four-velocity, d2xi/ds2 = dui/ds is the four-acceleration of the particle, we can consider the quantity
-miklukul as the "four-force", acting on the particle in the gravitational field. Here, the tensor gik plays the role of the "potential" of the gravitational field - its derivatives determine the field strength ikl.

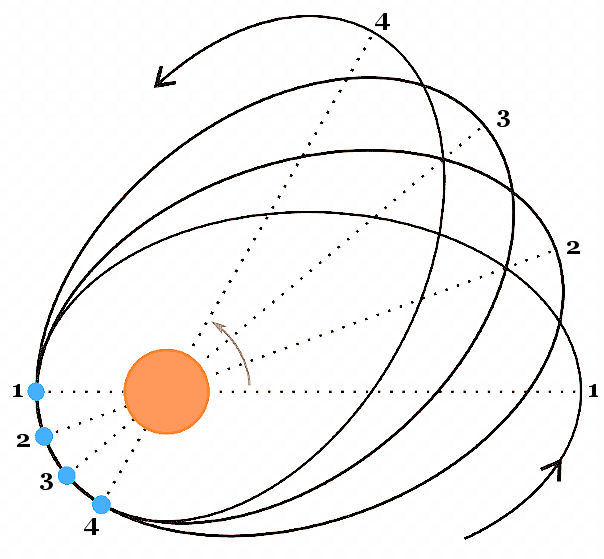Perihelion Advance Using the gravitational field equation and the equation of motion, Einstein presented a calculation on the effect of GR on the advance of the perihelion of Mercury:

= 6GM/(c2a(1 - e2)) ---------- (12e)

where M is the mass of the Sun, a is the length of the semi-major axis, and e is the eccentricity of the ellipse. In Figure 08, the amount of the advance is greatly exaggerated. The actual advance due to the effect of GR is only 0.43 seconds of arc per year. The most recent and most accurate results seem to be converging towards a value that makes the GR predictions agree well with observation.

Figure 08 Perihelion Advance [view large image]
The example above is just one of the most remarkable predictions substantiated by observation. In fact, no observation has ever been made anywhere in nature which conflicts with general relativity. However, the equations also admit weird solutions, which defy common sense. Thus, among all the successful examples it comes with other more puzzling possibilities as commented by Michio Kaku:

Einstein's equations, in some sense, were like a Trojan horse. On the surface, the horse looks like a perfectly acceptable gift, giving us the observed bending of starlight under gravity and a compelling explanation for the origin of the universe. However, inside lurk all sorts of strange demons and goblins, which allow for the possibility of interstellar travel through wormholes and time travel. The price we had to pay for peering into the darkest secrets of the universe is the potential downfall of our most commonly held beliefs about our world - that its space is simply connected and its history is unalterable.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.