Relativity, Cosmology, and Time

Schwarzschild's Solution and Black Hole (2018 Edition)

• Flat Space Approximation - For r >> r_s, the space-time metric reduces to the expression for flat space-time:
  
  ds² = c²dt² - dr² - r² (sin² d² + d²) ---------- (13a)
  


• Newtonian Limit - At weak field and non-relativistic limit where v²/c² << 1, it can be shown that the the gravitational potential in classical mechanics and the metric tensor g₀₀ in general relativity is linked by the formula :
  
  g₀₀ = 1 + 2/c² ---------- (13b).
  
  Specifically, by comparing to the Schwarzschild metric in (Eq.13)
  
  = -GM/r or in term of the gravitational force (applied on m, exerted by M) F = -m(d/dr) = -GMm/r² ---------- (13c) ,
  
  which are just the usual gravitational potential and force for point mass M in classical mechanics. It also reveals that at the non-relativistic limit only the time dilation effect (relating to g₀₀) is important. The effect of spatial curvature (relating to g₁₁) is negligible at this point.
  
  
• Interior Solution - Eq.(13) is not the only solution for the case of a centrally symmetric field. Inside a sphere of material with boundary R, density , and total mass M, the space-time metric (neglecting the angular parts) is in the form (Figure 08a,a) :

  Figure 08a Schwarzschild Metric - Interior, Critical Point, Black Hole [view large image]

  
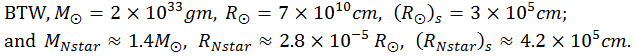  In equilibrium, the pressure gradient dp/dr provides just enough opposition to the gravitational inward crush as shown in the equation below :

  Figure 08b1 Polytropic Equation of State [view large image]

  Also see another scale of the Sun's density (Figure 08b2), which emphasizes the near constant profile. This equation is for the case of hydrostatic equilibrium in ordinary stars where the stability is maintained by nuclear burning (Figure 08c2). The full-fledged version goes by the moniker of Tolman-Oppenheirmer-Volkoff (TOV) equation which includes both the special relativistic effect in p/c2 and the general relativistic effect in 1/[r-rs(m/M)]. The equation becomes invalid when the star fails to generate outward pressure to counter the inward crush by gravity.

  Figure 08b2 Sun's Density Profile [view large image]

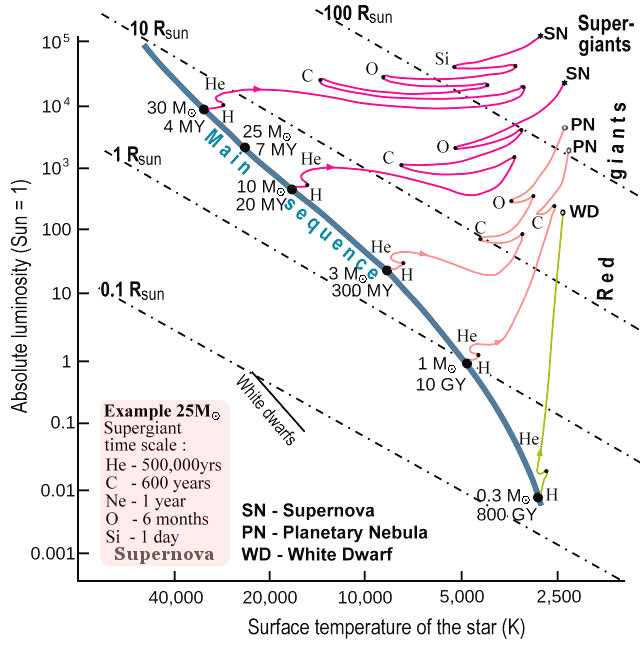
  		For example, the maximum mass supported by electron degeneracy is 1.4 Msun in white dwarf with R ~ 6x108cm, rs ~ 4x105cm. On the other hand for neutron star, it is estimated that nuclear repulsion can up hold a maximum of about 2 Msun. At R ~ 6.6x105cm and rs ~ 6x105cm, AR2 = rs/R = 0.9, density ~ 5x1015 gm/cm3, such star is at the limit of hydrostatic balance (see Figure 08d). It lasts for a long long time.
  Figure 08c1 Interior of the Sun [view large image]	Figure 08c2 Hydrostatic Equilibrium	In Figure 08c1, 1 bar = 10-6 dynes/cm2 = 10-6 gm/cm-sec2, 1 bar/c2 ~ 10-15 gm/cm3.

  
  

  		Critical Point (Figure 08a,b) - Supergiant stars of mass ~ 25 Msun undergoes successive shell burning with decreasing time scale as indicated in Figure 08e. Eventually, it generates an iron core which could not provide thermal pressure to support the crushing gravity. The collapse is delayed for a short while by degeneracy pressure of electrons and then neutrons (see Figure 08d). When the density reaches to about 6.6x1015 gm/cm3, the core approaches to the critical radius R = rs ~ 6x105 cm (for a final mass of about 2 Msun). At this point the gravitational force becomes infinity as shown by the TOV equation.
  Figure 08d Eq. of State, Cold-Dead Matter [view large image]	Figure 08e Post-Main-Sequence [view large image]	There is nothing that can stop the collapse to black hole. The event occurs while the star is still a supergiant, the remaining hydrogen-rich atmosphere is ejected during the process known as type II supernova.

  
  
• See "Black Hole Interior"



• Black Hole Space-time - The fate of the collapsing matter is supposed to be compressed into a point at infinite density according to conventional wisdom. Other possibilities include : (1) more levels of degeneracy support such as from the quarks (see quark star) or the hypothetical preons (see Preon Star); (2) the unknown effect of quantum gravity, (3) and then the Penrose universes via rotating black hole. Anyway theory dictats that once the ball of matter falls inside the Schwarzschild radius r_s, space-time is separated into two regions outside and inside r_s with distinct properties as described below (and depicted in Figures 08f and 08g) :

  		The Schwarzschild metric approaches to the Minkowski form when r >> rs. For the ds = 0 null line, the speed of incoming light dr/dt = -c(1 - r/rs) 0 as r rs. Thus, light cannot get inside according to a distant observer. Inside rs, dr/dt changes sign - the incoming becomes outgoing. The speed of light dr/dt at r = 0 is infinity, and approaches 0 as r rs. That's the popular notion about light cannot get out from inside the black hole.
  Figure 08f BH Space-time	Figure 08g Black Hole and White Hole Light Rays [view large image]	Similar effect causes outgoing light to propagate out slowly from rs, and plunging into the center inside rs with dr/dt as r 0.

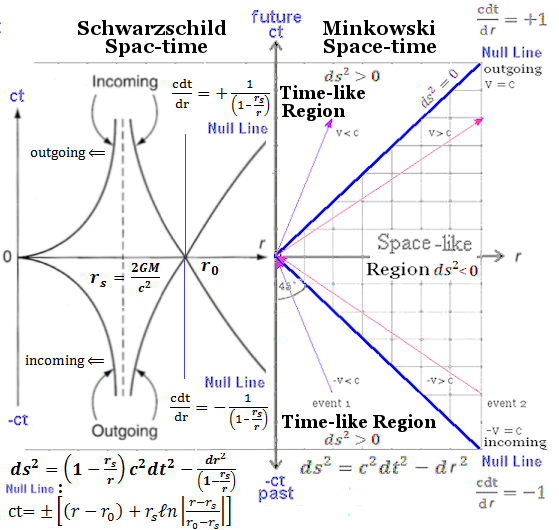
  • From the geodesics equation for particle with mass, the time reaching r_s from R₀ is given by
    t = -(r_s/c)n[(r - r_s)/(R₀ - r_s)] ---------- (13d)
    showing the similar effect of slowing down (of light speed) as r r_s.
  • However, for a plunging (local) observer toward the black hole with his/her own clock, the proper time
    
    which shows that it takes a finite time to reach any point including r_s and r = 0.
  • Integrating the null line equation for light propagation
    c(dt/dr) = 1/(1 - r_s/r)
    yields (- sign for incoming, + sign for outgoing, see Figure 08f) :
    t = (1/c)[(r - r₀) + r_sn|(r - r_s)/(r₀ - r_s)|] ---------- (13e)
    where r₀ corresponding to time t = 0 outside r_s (see Figure 08f). This formula is almost identical to Eq.(13d) for particle with mass.
  • Defining a new time coordinate
    cT = ct + [r_sn|(r - r_s)/(r₀ - r_s)|],
    we obtain :
    c(dT/dr) = r/(r - r_s) + r_s/|(r - r_s)| ---------- (13f).
    Thus, for the incoming ray
    c(dT/dr) = -1,
    it goes straight through r_s to r = 0. The situation is similar to the local observer using his/her own clock, although there is no such thing as proper time for light (since cd = ds 0).
    However, according to the other solution for the going ray near r_s,
    c(dT/dr) = (r + r_s)/(r - r_s)
    it approaches the normal speed c(dT/dr) = +1 outside for r >> r_s, but becomes an incoming ray inside (see Figure 08g). This form is similar to the view of distant observer in Figure 08f.
    Therefore, the time T represents both views of local and distant observers of the black hole. This is sometimes referred to as "tortoise time" since it takes a long long time to get out just outside the event horizon according to the distant observer.
  • Defining another new time coordinate with the replacement of the "+" to "-" sign
    cT = ct - [r_sn|(r - r_s)/(r₀ - r_s)|],
    we obtain :
    c(dT/dr) = r/(r - r_s) - r_s/|(r - r_s)| ---------- (13g).
    Thus, for the outcoming ray
    c(dT/dr) = +1,
    it goes straight through from the center to infinity. This is the local observer's view using his/her own clock. Such object is called the white hole splitting out light and matter in opposite to the black hole which grabs up everything.
    However, according to the other solution for the incoming ray near r_s,
    c(dT/dr) = -(r + r_s)/(r - r_s)
    

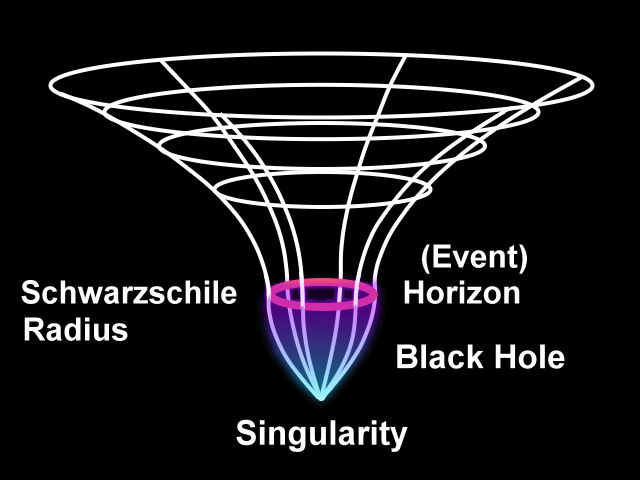
    	it starts with the normal speed c(dT/dr) = -1 outside for r >> rs, but becomes outgoing ray inside from the center (see Figure 08g). This locus is similar to the view of distant observer in Figure 08f. Therefore, this time T represents both views of local and distant observers of the white hole, which is not yet observed in this world.
    Figure 08h White Hole [view large image]	Figure 08h is an embedding diagram of a white hole - the upside down version of the black hole in Figure 09a. Also see "wormhole".

  
  

  		Embedding Diagram - The concept of black hole is often evolved by the escape velocity ve = (2GM/r)1/2 = c at r = rs = 2GM/c2 from inside. It implies that even light cannot escape the grip of gravity at this point. Figure 09a is an embedding diagram of a black hole as its most popular visual image. Actually, the hole within the circle is not physical, it depicts only the curvature of space (inversely proportional to the size of circle). In Figure 09b, the 2-D circles are the projection of 3-D spheres - the hyperspace. The vertical lines denote the "stretch" of space (proportional to the length) as a function of the radius r.
  Figure 09a Black Hole, 3-D Spatial Curvature [view large image]	Figure 09b 2-D Embedding Diagram

  
  

  Gravitational redshift is generated as the photons loss energy in overcoming the pull of the gravitational field (see Figure 09c). For the case of a black hole, the shifted wavelength is computed by the formula: = o / (1 - rs/r)1/2 where r is the distance of the light source with respect to rs, and the observer is assumed to be at infinity. The redshift becomes infinity when r = rs. This is the effect that makes light invisible with the source at rs.

  Figure 09c Redshift [view large image]

  On the other hand if the positions of the source and observer are switched, the wavelength will be blue shifted according to the formula: = (1 - rs/rob)1/2 o. There would be no change of wavelength if both observer and source are falling together into the black hole.

• Time Dilation - The gravitational field also induces time dilation as experienced by a far away stationary observer. It is in a similar form:
  
  T = T_o (1 - r_s/r)^1/2
  
  

  		where T is the time interval recorded by an observer plunging toward the black hole and To is the corresponding time perceived by a stationary observer. Thus, for the stationary observer it takes an infinite long interval for the other observer approaching the Schwarzschild radius rs. However, the adventurer is not aware this curious effect on the time interval. His journey may be interrupted only by the tidal force, which is much more ferocious for black hole with smaller size (the tidal force at rs is equal to 2GM / rs3 = c6/(2GM)2, the + and - signs represent the stretch and squeeze parallel and perpendicular to the radial direction respectively, see Figure 09d). Figure 09e shows the time dilation for a space traveler located at a distance of 1.1 rs from the center of a black hole. The mass of the Earth M 6x1027 gm giving rs 1 cm. With the Earth's surface at about 0.63x109 cm, and the GPS satellite about 2.65x109 cm from the center, the % difference of clock rate between the two locations is about 50x10-9 (with respect to T0), which is one of the corrections that has to be made in order to produce an accurate map reading.
  Figure 09d Tidal Force	Figure 09e Time Dilation

  
  
• Wormhole Hole - It is the link between the black hole and white hole. The space-time metric for a static wormhole (also known as the Einstein-Rosen Bridge) can be expressed in the form :
  

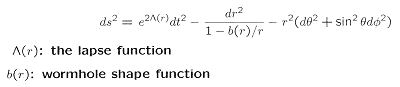  ---------- (15a)

  The lapse function defines the proper time as function of r; while the shape function determines the shape of the worm hole. The shape function takes on a very simple form for the case of the Schwarzschild's metric, i.e., b(r) = 2GM / c2 = rs. The throat of the wormhole is located at r = b(r) = rs in this case. Figure 09h is a computer generated embedding diagram of a blackhole, a wormhole, and a whitehole. The surface of the diagram measures the curvature of space. Color scale represents rate at which idealized clocks measure time; red is slow, blue fast.

  Figure 09h Wormhole [view large image]

  Another way to conceptualize a wormhole topology is to have the spatial part of the space-time metric in Eq.(15a) imbedded in a flat hyperspace with the extra-dimension denoted by W:

  		dl2 = dW2 + dr2 + r2 (sin2 d2) = dr2 / (1 - rs/r) + r2 (sin2 d2) ---------- (15b) Eq.(15b) can be used to equate dW = (r/rs - 1)-1/2dr. Integration of the equation gives W2 = 4rs(r - rs), which is a parabola function with vertex at W = 0, r = rs. Sweeping the curve around the W axis to include all values of from 0 to 2 results in a paraboloid surface as shown in Figure 09i.
  Figure 09i Worm- hole in Hyperspace [view large image]	Figure 09j Worm- hole Throat [view large image]

  
  Inside the wormhole, g₁₁ and g₄₄ change sign as shown in Eq.(13). The region becomes space-like, which means two events cannot be linked unless the signal propagates with greater than light speed. This peculiar property is also related to the instability of the wormhole. However it is suggested that if there is a large amount of negative mass/energy -m (in the forms of a thin spherical shell, which appears in the embedding diagram as the yellow circle as shown in Figure 09j) to sustain the structure, then creation of a

  		wormhole may become feasible. The negative mass ensures that the throat of the wormhole lies outside the horizon (since the new event horizon is now 2(M-m)G/c2), so that travelers can pass through it, while the positive surface pressure of such exotic material would prevent the wormhole from collapsing. This would allow for shortcut in space travel within the wormhole between two distant points (Figure 09k), or for the possibility of time travel courtesy of LHC (Figure 09l).
  Figure 09k Space Travel [view large image]	Figure 09l Time Travel [view large image]

  
  

Go to Next Section
 or to Top of Page to Select
 or to Main Menu