Relativity, Cosmology, and Time

Kerr's Solution and Rotating Black Hole

---------- (15c)

Since most collapsing massive objects would have some initial angular momentum, the Kerr's metric seems to be a more realistic representation for the black hole space-time. However, it is argued that the collapsing object would lost its rotational energy in the form of gravitational wave and ends up in a perfect spheroidal shape. Whichever to be the case, followings are some comments on the Kerr's metric and its modification to the Schwarzschild's black hole:


• At r , the Kerr's metric reduces to the one for flat space-time (same as Eq.(14)):
  
  ds² = c²dt² - dr² - r² (sin² d² + d²) ---------- (15g)
  
  
• The Kerr's metric reduces to the Schwarzschild's metric in Eq.(13) naturally when a = 0, i.e., with no rotation.
  
  

It was shown theoretically that light ray is deflected by gravitational field, e.g., binding of distant star light near the sun (see Figure 09m). The angle of deflection can be computed from the equation of motion Eq.(12b), or from the equation of energy conservation: = 4GM/Rc2, where M is the mass of the source and R is the distance from the source. At the surface of the Sun, = 1.75" (derivation from Newtonian mechanics is half as much). This prediction was confirmed by Sir Arthur Eddington's 1919 solar eclipse expeditions. If the light ray comes close enough to a dense

Figure 09m Bending of Light [view large image]

object, the path will be bent so much that it runs around in a circle. For non-rotating black hole such special trajectory occurs at r = 3rs/2 = 3GM/c2. The sphere with such a radius is called the photon sphere. However, the orbit is unstable; it can be

disrupted with very small perturbation. This precarious orbit is derived from the condition d²r / d² = 0. There are two photon spheres for the rotating black hole - an outer one for light ray traveling in a direction opposite to the spin of the black, and an inner one for co-rotating light ray.


• As r descends further toward the center, the space-time metric g₄₄ (or g_tt) vanishes at
  
  r = [GM + (G²M² - a²c²cos²)^1/2] / c² ---------- (15i)
  
  

  This is called static limit. It can be intuitively characterized as the region where the rotation of the space-time is dragged along with the velocity of light. Within this region, space-time is warped in such a way that no observer can maintain him/herself in a non-rotating orbit, but is forced to become co-rotating (Figure 09n). The surface of this region is elliptical with its major axis at = /2 (the equator), and r = 2GM / c2 (= the non-

  Figure 09n Frame Dragging [view large image]

  rotating Schwarzschild's radius). The minor axis is in the directions of = 0, and (the poles), and r = [GM + (G2M2 - a2c2)1/2] / c2 (see Figure 09o).

  It is found in 2006 that a spinning superconductor generates a much larger drag than that from a regular rotating mass. The effect is attributed to some sort of "gravitomagnetism" (Figure 09n, no relation to electromagnetism) produced by massive gravitons similar to the Meissner effect produced by massive photons. The discovery may fulfill the "anti-gravity device" perpetrated by science fictions.
  
  

  	A rotating black hole is very different from a Schwarzschild black hole in that the spin of the black will cause the creation of two event horizons instead of just one (see Figure 09o). The outer event horizon occurs at r+ = [GM + (G2M2 - a2c2)1/2] / c2 ---------- (15j) The inner horizon (sometimes called the Cauchy horizon) is located at r- = [GM - (G2M2 - a2c2)1/2] / c2 ---------- (15k)
  Figure 09o Kerr's Solution [view large image]	The Ergosphere is the region between the static limit and the outer event horizon. Since this region is outside the event horizon, particles falling within the ergosphere may escape the black hole extracting its spin energy in the process.

  The separation between the two horizons is 2 (G²M² - a²c²)^1/2 / c². For a = 0, r_- =0, hence for a non-rotating black hole, the inner event horizon can be considered as fallen into the center. As the spin increases, the two horizons move toward each other and merge at r = GM / c² when a / c = GM / c². In case a / c > GM / c², there will be no event horizon, the black hole becomes a "naked singularity", i.e., it is not covered by an event horizon.

  The mere thought of such possibility makes a lot of physicists very uncomfortable. Nevertheless, the Penrose's conjecture on cosmic censorship, which forbids the occurrence of naked singularity, may not hold up any longer in view of the Kerr's solution and more recently the revelation of computer simulations (with one such results shown in Figure 09oa). Other stellar configurations that can develop into naked singularity; include inhomogeneous density (such as onionlike structure), shearing of material near a singularity, and very rapid collapsing rate. Each of such

  Figure 09oa Naked Singularity [view large image]

  case has a threshold separating the formation of black hole or naked singularity.

  Note 1: The only physical part of a black hole is the singularity. The static limit, and event horizon are not physical barrier; they only mark the imaginary boundaries between types of space.
  Note 2: A proposal in 2007 suggests that naked black hole should be detectable via the "gravitational lenses" effect. Existing telescopes should have sufficient spatial resolution to spot naked singularities in the center of the Milky Way. Other methods rely on special signatures from high-energy explosions, gamma-ray bursts, and spinning rate.




Talking about black hole spinning rate, by measuring the line broadening of the Fe-line emission in the X-ray region it is reported in 2013 that the central black hole in NGC 1365 spins rapidly near to the naked black hole limit (Figure 09ob), which can be expressed in the form : 1 > Jc/GM2 = A, where J is the black hole's angular momentum and A 1 for a naked black hole. Various models with different parameters (such as disk inclination, ionization state and emissivity profile) were run to match the observed data. The minimum spin was found to be A 0.84 at 90% confidence. The maximum rate is A = 0.97 when the disk inclination is limited to 55-60o. Beside boosting the case for cosmic censorship, this result indicates that the black hole acquires the angular momentum from a small number of feeding events. The black hole formation process is intimately linked to galactic evolution.

Figure 09ob BH Spin in NGC 1365 [view large image]

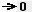• As r , a singularity develops in the form of a ring at the equator (see Figure 09p), where /2, and cos 0 in such a way that r > (a / c) cos. The Kerr's metric then becomes:
  
  ds² = (1 - 2GM / c²r) c²dt² - (2GMa / c²r) dt d - (a²/c²) (1 + 2GM / c²r) d² ---------- (15n)
  
  The severity of the singularity depends on the angular momentum per unit mass a. If a is sufficiently large it would be very mild; on the other hand it becomes a point singularity at the limit a 0. Away from the ring of singularity in the region where r ~ 0, the Kerr's metric has the form:
  
  ds² = c²dt² - cos² dr² - (a²/c²) (cos² d² + sin² d²) ---------- (15o)
  
  Interesting theoretical physics can take place around this ring singularity. Since 1 g₁₁ = cos² in Eq.(15o), the spatial curvature is negative, which acts like a repulsive force. One consequence is that nothing can actually fall into this region unless approaching in a trajectroy along the ring's side. Any other angle and the negative spatial curvature actually produces an antigravity field that repels matter. It could be the mechanism that produces the jets observed in many black holes.




The Penrose diagram in Figure 09p summarizes all regions of space-time associated with a rotating black hole. A penrose diagram is not meant to accurately portray distances, it describes only the causal structure. Only radial and time directions are represented while angular directions are suppressed. The units of space and time are scaled in such a way that any object moving at the speed of light will follow a path at an angle of 45o to the vertical. All possible paths for physical objects must stay closer than 45o to the vertical. The green diamond represents our entire Universe over its entire history and destiny, from the infinite past to the infinite future (it takes an infinite amount of time to cross the outer event horizon from the view point of a distant observer). The purple diamond is the region between the outer and inner event horizons, where everything plunges inward. The red area denotes the space between the inner event horizon and the ring singularity, where the space-time re-acquires its normal characteristic with rising curvature toward the ring singularity. The other half in yellow is the region inside the ring singularity, where the gravity becomes repulsive. The blue diamonds can be interpreted as another universes or another part in our own universe. This concept is similar to the wormhole in the Schwarzchild's solution.

Figure 09p Penrose Diagram [view large image]

As depicted in the Penrose diagram, the space-time metric g11 (or grr) changes sign when crossing over the first event horizon, and then reverses back again at crossing over the second horizon. Thus between the two horizons, space and time exchange places. Instead of time always moving inexorably onward, the radial dimension of space moves inexorably inward to the Cauchy horizon. After that the Kerr solution predicts a second reversal, which implies no more plunging inward. In this strange region inside the Cauchy horizon the observer can, by selecting a particular orbit around the ring singularity, travel backwards in time and meet himself, in violation of the principle of causality (cause must precede effect). It is surmised that a closed time-like curve (CTC, Figure 09q) to loop back to the past is possible in a heavily curved space-time (Line A in Figure 09p). Another possibility admitted by the equations for the observer in the central region is to plunge through the hole in the ring into an antigravity region (Line B). Or he can travel through two further horizons (or more properly anti-horizons), to emerge at coordinate time t = - into some other universe (Line C). These exotic properties of rotating black holes have inspired several science fiction stories.

Figure 09q Closed Time-like Curve (CTC)





A more realistic rotating black hole would have an accretion disk around the equator and a pair of jets ejecting along the poles. An accretion disk is matter that is drawn to the black hole. As matter is gradually pulled into the center, it gains speed and energy. It can be heated to temperatures as high as 3 billion K by internal friction, and emit energetic radiation such as gamma rays. Some of the particles that has funneled into the disk-shaped torus by the hole's spin and magnetic fields, can escape the black hole in the form of high speed jets along the poles (Figure 09ra).

Figure 09ra Disk and Jets [view large image]

Black Holes are very difficult to detect because they are black. It would be a definitive proof of their existence if we can see the "shadow" in the form of a dim spot in the centre of the glowing accretion disc (Diagram c in Figure 09rb). Most of the circumstantial evidences come from observing high velocity objects moving tightly in small space as shown in Diagram a, Figure 09rb. Other evidences involve detecting gravity waves from merging black hole(s) or the double image from a spinning black hole (see Diagram b and d in Figure 09rb), which throws out huge jets of debris to advertise its presence. The final answer to whether our black hole ideas are correct would be sending a probe to a nearby candidate and have it transmit data as it makes its final plunge.

Figure 09rb Black Hole Detections

• Black holes are characterized by mass and spin. It has been known long time ago that the mass can be calculated from the speed of orbiting materials. Estimation of spin is more difficult until recently when it is possible to examine the X-rays from the accretion

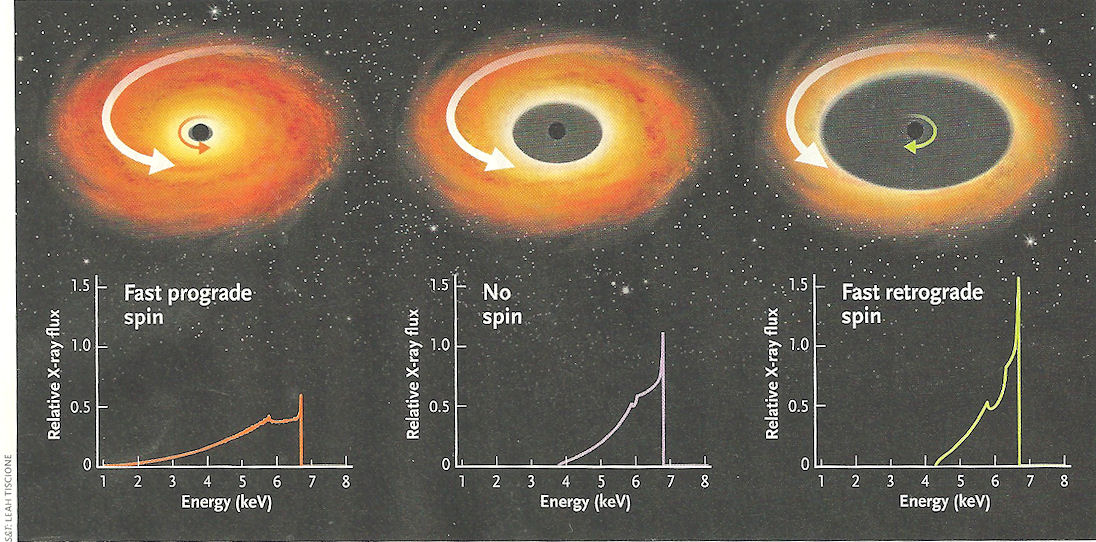  disk's innermost edge. One of the techniques is to observe the line profile of the Fe K emission line at 6.4 kev. As shown in Figure 09rc, the broadening of the emission line depends on whether the accretion disk is co-rotating (prograde spin), anti-rotating (retrograde spin), or the hole is not spinning. The extent of broadening is determined by both Doppler and gravitational shifts. However, the total shift is always toward the red (lower energy) as the latter effect always overwhelms the former. The spin of the black hole can be determined by constructing spectral models that take relativity into account. The spin is directly related

  Figure 09rc Black Hole Spin [view large image]

  to the location of the disk's inner edge. Table 02 lists the spin for a few of the black holes. The spin s in the table is relative to the tangential velocity v = c (the speed of light), i.e., s / sc = v / c (at the event horizon).

  
  

  Black Hole	Spin	Astronomical Characteristics
  GRS 1915	0.98 0.01	Micro-quasar (a 33 Msun black hole acting like a quasar)
  Cygnus X-1	0.05 0.01	X-ray Binary (stellar black hole + O star)
  MCG-6-30-15	> 0.98	Bright core of spiral galaxy
  NGC 7469	0.69 0.09	Interacting galaxy
  Markarian 335	0.70 0.12	Seyfert galaxy

  Table 02 Spin of Some Black Holes

  Some peculiar properties of the black hole have been unveiled by studying its spin :
  
  
  1. It is found that black holes that grow primarily by accretion will spin faster than those that grow mostly by mergers with other black holes as the latter case happened at random orientations, which most likely would not impart substantial angular momentum to the spin of the system.
  2. Rotational energy of the spin can be converted to jets, which shoot out like geysers from the core. It is thought that magnetic field plays a crucial role in the process.
  3. Theoretical study concludes that retrograde-spinning can power jets up to 100 times stronger than their prograde counterparts. However, retrograde spin only persists for a short fraction of the lifetime of the super-massive black holes consisting with the rarity of such phenomenon.
  
  There are plenty of unanswered questions about the role of spin in other aspects such as the accretion rate, the evolution of the galaxy, its relationship with mass, and its distribution among the super-massive and stellar black holes.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu