
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
 |
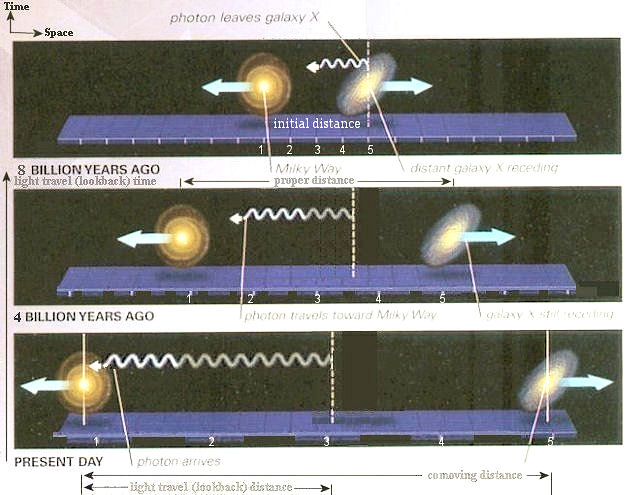
where v is the recessional velocity (in km/sec) of the astronomical object due to the expansion of the universe (Figure 11a), D is the proper distance (in mega parsecs = Mpc) to the same object including the effect due to the expansion (Figure 11b), and H0 is called the Hubble constant, which is in unit of (km/sec)/Mpc and can be interpreted as the increase in expanding velocity for every Mpc from the observer. The inverse of H0 is equated to the age of the universe ~ 13.8 Gyr (see more accurate formula). |
Figure 11a Cosmic Expansion |
Figure 11b Proper Distance [view large image] |
A recent practice often expresses H0 = 100h (km/sec)/Mpc with the dimensionless h 100 times smaller than H0, i.e., h = H0/100[(km/sec)/Mpc], h = 0.7 is the popular choice. |
 e /
e /  0) - 1 = v/c, where
0) - 1 = v/c, where  e is the red shifted wavelength,
e is the red shifted wavelength,  0 is the wavelength of the original spectral line; while the proper distance D is obtained by Parallax or Cepheid Variables of those "Standard Candles" closer to Earth. In term of z, the Hubble's Law can be expressed as z = (H0/c)D = D/DH, where DH = c/H0 is the cosmic horizon. This formula is valid only for D << DH.
0 is the wavelength of the original spectral line; while the proper distance D is obtained by Parallax or Cepheid Variables of those "Standard Candles" closer to Earth. In term of z, the Hubble's Law can be expressed as z = (H0/c)D = D/DH, where DH = c/H0 is the cosmic horizon. This formula is valid only for D << DH. |
 |
For objects further away, the standard candles (Figure 11c) usually invokes the magnitude-distance relation to calculate D : m = M - 97.5 + 5xlog(D), where m is the apparent magnitude which can be measured directly, M is the absolute magnitude, which is unique for a special class of astronomical obejcts. The distance D can be calculated from the above formula once M is known. |
Figure 11c Standard Candles |
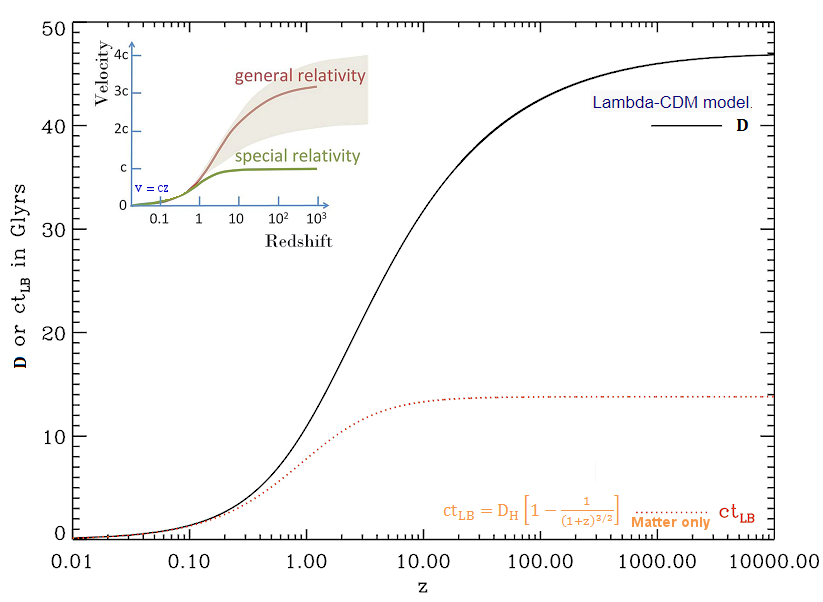
Figure 11d lambdaCDM Model [view large image] |
As shown in Figure 11d, neither the naive v = cz nor the special relativistic expression : v = c[(1 + z)2 - 1] / [(1 + z)2 + 1] is suitable as they have not taken the cosmic expansion into account. |
 2 + sin2
2 + sin2 d
d 2)).
2)). = 0, d
= 0, d = 0, the proper distance is defined by : dD = R(t)dr.
= 0, the proper distance is defined by : dD = R(t)dr.  dD = R(t)
dD = R(t) dr = R(t)r, where r is the initial separation (distance) of the two objects and does not change over time.
dr = R(t)r, where r is the initial separation (distance) of the two objects and does not change over time. e at time te, then dt = [(te +
e at time te, then dt = [(te +  e/c) - te] =
e/c) - te] =  e/c; similarly the observer would receive the red shifted wave with dt =
e/c; similarly the observer would receive the red shifted wave with dt =  0/c . Equating the ratio yields
0/c . Equating the ratio yields  e/R(te) =
e/R(te) =  0/R(t0), thus :
0/R(t0), thus :  0 /
0 /  e) = R(t0)/R(te), or
1 + z = 1/R(t) with the usual convention of equating R(t0) = 1 and re-labeling te to t. It is through this relation the cosmological models are linked to the red shift z (Figure 11d).
e) = R(t0)/R(te), or
1 + z = 1/R(t) with the usual convention of equating R(t0) = 1 and re-labeling te to t. It is through this relation the cosmological models are linked to the red shift z (Figure 11d). |
(dR/dt)2/R2 = H(R)2 = (H0)2( M/R3 + M/R3 +  k/R2 + k/R2 +   ) ---------- Eq.(2), ) ---------- Eq.(2),where  M = 8 M = 8 G G M/3 H02, M/3 H02,  k = -kc2/ H02, k = -kc2/ H02,   = =  c2/3 H02 are the density parameters, and c2/3 H02 are the density parameters, and  M is the baryonic M is the baryonic  B + dark matter B + dark matter  DM denstiy, k the spatial curvature, DM denstiy, k the spatial curvature,  the cosmological constant as dark energy (all of them for the current epoch). This combination consists the modern Standard Cosmological Model called the cosmological constant as dark energy (all of them for the current epoch). This combination consists the modern Standard Cosmological Model called  CDM model. The red curve in Figure 11e is the solution with CDM model. The red curve in Figure 11e is the solution with  M = 0.3, M = 0.3,   = 0.7 and k = 0. = 0.7 and k = 0.
|
Figure 11e Cosmological Models [view large image] |
 M(1+z)3 +
M(1+z)3 +  k(1+z)2 +
k(1+z)2 + 
 )1/2] dz, which can be interpreted as the infinitesimal change in the proper distance corresponding to the infinitesimal change in expansion speed dv or dz. The comoving distance Dc = D(t0) is just the sum of dD to z =
)1/2] dz, which can be interpreted as the infinitesimal change in the proper distance corresponding to the infinitesimal change in expansion speed dv or dz. The comoving distance Dc = D(t0) is just the sum of dD to z =  to 0, while the proper distance is :
to 0, while the proper distance is : dz' / [
dz' / [ M(1+z')3 +
M(1+z')3 +  k(1+z')2 +
k(1+z')2 + 
 ]1/2 ---------- Eq.(3).
]1/2 ---------- Eq.(3). CDM model.
CDM model.
 |
Since ds = 0 for the photon cdt = dD, but it has to be modified by the Doppler effect due the cosmic expansion as well. Thus, an additional term is introduced into the equation, i.e., cdt + vdt = (1+z)cdt, or dDT = cdt = dD/(1+z) = R(t)dD ---------- Eq.(3a), DT = -DH  dz' / {(1+z')[ dz' / {(1+z')[ M(1+z')3 + M(1+z')3 +  k(1+z')2 + k(1+z')2 +   ]1/2} ---------- Eq.(3b). ]1/2} ---------- Eq.(3b).The original Hubble's Law is recovered for z ~ 0, i.e., DT ~ Dc = D(t0) ~ cz/H0 or V(t0) ~ H0D(t0). The age of the universe is computed from DT integrating from z  to 0, it is not exactly equal to 1/H0 (see Figure 11u). to 0, it is not exactly equal to 1/H0 (see Figure 11u).
|
Figure 11e1 Cosmic Distance |
Figure 11e1 is another attempt to explain the subtlety of Cosmic Distances. See also "Types of Cosmic Distance". |
 CDM models (in term of comoving distance Dc vs z) with observational data. The supposedly linear relationship between velocity and red shift is distorted by :
CDM models (in term of comoving distance Dc vs z) with observational data. The supposedly linear relationship between velocity and red shift is distorted by :  dz' / [
dz' / [ M(1+z')3 +
M(1+z')3 +  k(1+z')2 +
k(1+z')2 + 
 ]1/2 ---------- Eq.(4)
]1/2 ---------- Eq.(4)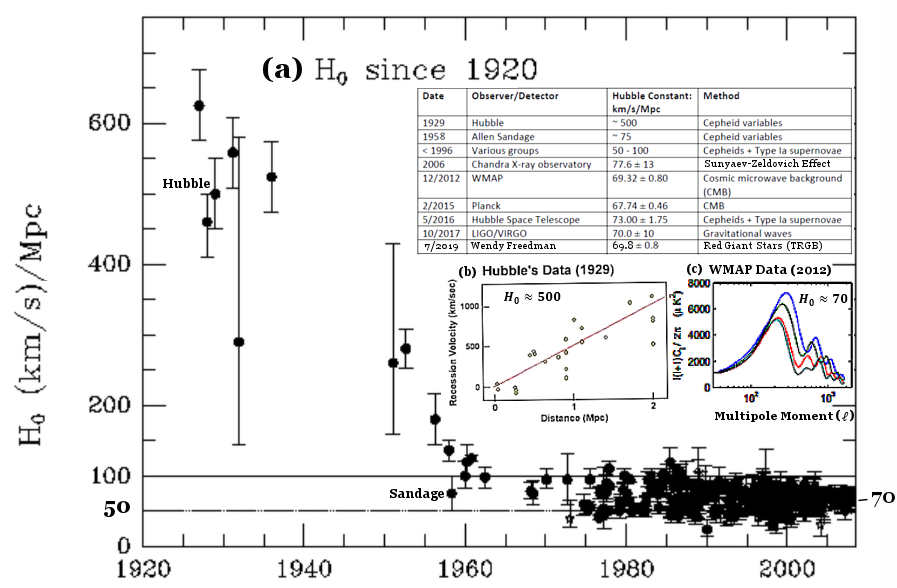 |
 |
 i( i( i) = 1. i) = 1. |
Figure 11f Measurements of H0 |
Figure 11g Modern Hubble Diagram [view large image] |
 |
 |
Figure 11h illustrates how to adjust the input parameters to match a theoretical model to the observational data, which are measured by WMAP. The demonstration software is supplied by NASA's "Build a Universe". The Blue curve is the result of the "best fit". The official value for H0 is actually ~ 71 (km/sec)/Mpc (instead of 73 in the demonstration run, see "WMAP parameters"). The ESA/Planck team has its own "Cosmological parameters", which quotes a H0 value of 67.7 (km/sec)/Mpc - a rather substantial difference from the WMAP's estimate (see Tension). The latest estimate of H0 ~ 70 (km/sec)/Mpc in 2019 is derived from the TRGB measurement. |
Figure 11h CMBR Analyzer |
Figure 11i CMBR, H0 Dependence |
Figure 11i shows the effect of varying the Hubble constant on the CMBR theoretical curve. The most affected portion is related to the time-dependent perturbations of the gravitational field at large scale. |
 |
(decoupling) time. Initially, it traveled with the CMBR together. It lost energy and stalled as the photons stream ahead faster. The sound horizon with a fixed radius (in comoving coordinates) then became a relic with higher matter density to produce more astronomical objects such as galaxies at that location which is estimated to be about 153 Mpc ~ 500 Mlyr from the point of origin. Detection of such feature would yield information on some of the cosmic parameters as shown below after a brief summary on its evolution (see visual aid in Figure 11l). |
Figure 11j BAO Horizon in Light Travel Distance |
Figure 11j shows the BAO horizon expanding with the cosmic expansion. |
 |
|
Figure 11k BAO in Comoving Coordinates [view large image] |
 |
 |
|
Figure 11l BAO Evolution of ONE Primordial Wavelet |
Figure 11m Density Correlation |
a peak in the diagram. There would be a lot of such spherical structures known as standard rulers mixing with other astronomical objects in certain part of the universe as the cosmos expanded (see Figure 11m2,a). |
 |

|
Figure 11m2 Hubble Parameter [view large image] |

|

 c2 , where
c2 , where  is the matter/energy density and p the pressure.
is the matter/energy density and p the pressure. CDM parameters
CDM parameters  M = 0.25,
M = 0.25, 
 = 0.75, and
= 0.75, and  and equation of state p/
and equation of state p/ c2 = w.
c2 = w. G
G /3 ,
/3 , 
 + 3[(dR/dt)/R](
+ 3[(dR/dt)/R]( + p/c2) = 0 ---------- Eq.(6),
+ p/c2) = 0 ---------- Eq.(6), G
G /3) (1 + 3w) ---------- Eq.(7).
/3) (1 + 3w) ---------- Eq.(7).
 until recently when the dark energy acceleration took over at z ~ 0.8 (see "Vacuum Energy Density").
until recently when the dark energy acceleration took over at z ~ 0.8 (see "Vacuum Energy Density"). =
=  0/R3(1+w) =
0/R3(1+w) =  0(1+z)3(1+w) ---------- Eq.(8).
0(1+z)3(1+w) ---------- Eq.(8).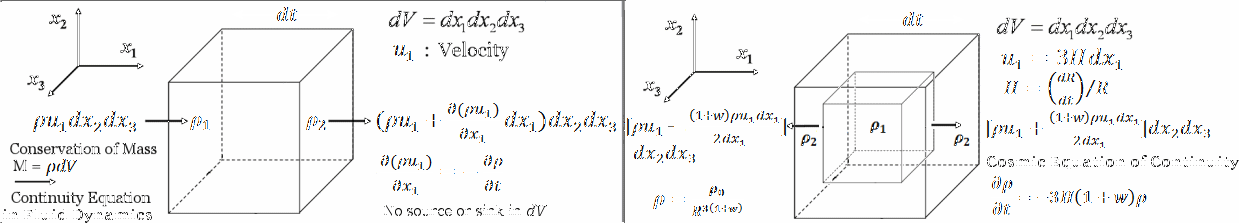 |
This is the rationale to replace   by by   /R3(1+w) as mentioned previously in BAO. Comparison with the equation of continuity in fluid dynamics shows that it is really not an equation for the conservation of mass (Figure 11n). It actually dictates the variation of the matter-energy density as the result of cosmic expansion. /R3(1+w) as mentioned previously in BAO. Comparison with the equation of continuity in fluid dynamics shows that it is really not an equation for the conservation of mass (Figure 11n). It actually dictates the variation of the matter-energy density as the result of cosmic expansion.
|
Figure 11n Continuity Equation |
It reveals that : |
 --------- Eq.(9a), or
--------- Eq.(9a), or ), or
), or  )/log(1+z)]} - 1 ---------- Eq.(9b),
)/log(1+z)]} - 1 ---------- Eq.(9b),  = [
= [
 (1+z)4 +
(1+z)4 +  M(1+z)3 +
M(1+z)3 + 
 ] .
] .

 1/R4.
1/R4.
 1/R3. It has been over taken by dark energy at z ~ 0.8 (R ~ 0.56).
1/R3. It has been over taken by dark energy at z ~ 0.8 (R ~ 0.56).  =
=  0 = constant. Matter-energy is somehow infused into the universe to keep
0 = constant. Matter-energy is somehow infused into the universe to keep  unchanged during the accelerated expansion - probably as "Vacuum Energy Density" from the newly created space in the expansion.
unchanged during the accelerated expansion - probably as "Vacuum Energy Density" from the newly created space in the expansion. |
 have to be taken into account to determine w as shown in Figure 11o, which is calculated by a Basic program have to be taken into account to determine w as shown in Figure 11o, which is calculated by a Basic program
|
Figure 11o w-parameter and cosmic density vs log(1+z) [view large image] |
running in lap-top computer. The computation is cut off at log(1+z) ~ 4, beyond which it returns the "out of range" error message. |
 vanishes except the dark energy, which then becomes the critical density and thus
vanishes except the dark energy, which then becomes the critical density and thus  = 1. The continuity equation could be satisfied only if w = -1 as shown by Eq.(9a).
= 1. The continuity equation could be satisfied only if w = -1 as shown by Eq.(9a). c2.
c2.
 |
 |
Figure 11p Cosmic Timeline [view large image] |
Figure 11q [view large image] Cosmic Parameters |
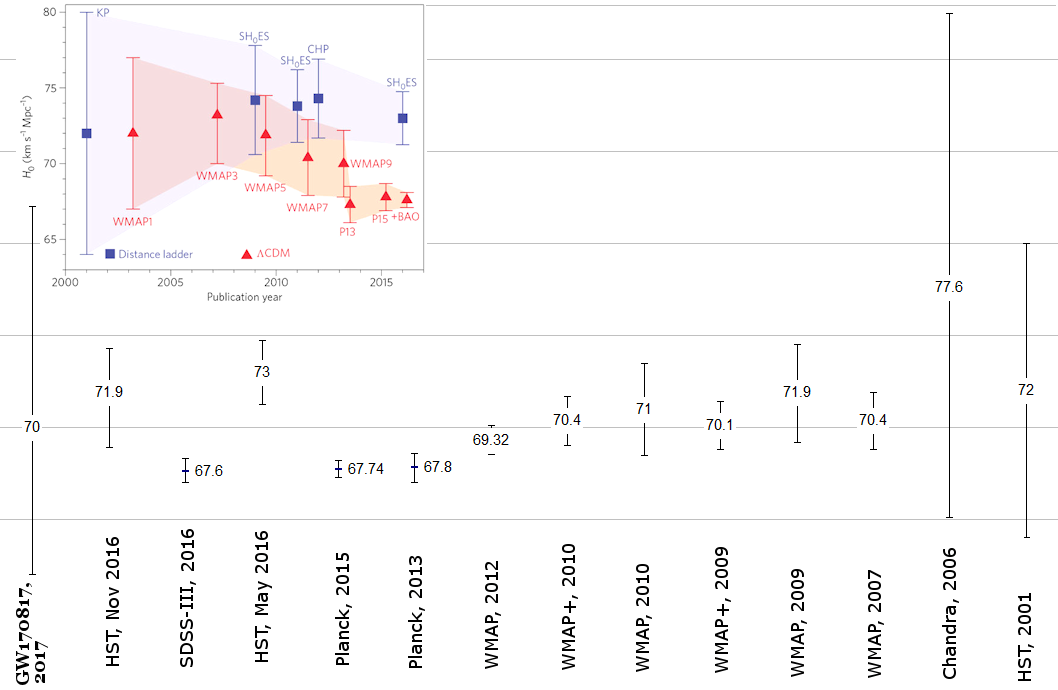 |
 |
Meanwhile, the SHOES Program (Supernovae and H0 for the Equation of State) have made precision measurement (<5%) of H0 by refining the SN and Cepheids observations. Their results are plotted in the insert of the same graph. There is a considerable discrepancy with the Planck's values after 2013 when the respective error bar would not overlap anymore. The measurement of the so called shear power S8 from the "KiDS-450 Weak Lensing Power Spectrum" has contributed additional tension with another |
Figure 11r Hubble Constant in 21st Century |
Figure 11s Shear Power S8 [view large image] |
substantial difference from the Planck's evaluation (Figure 11s). It demands an explanation (see "How Heavy is the Universe? Conflicting Answers Hint at New Physics"). |
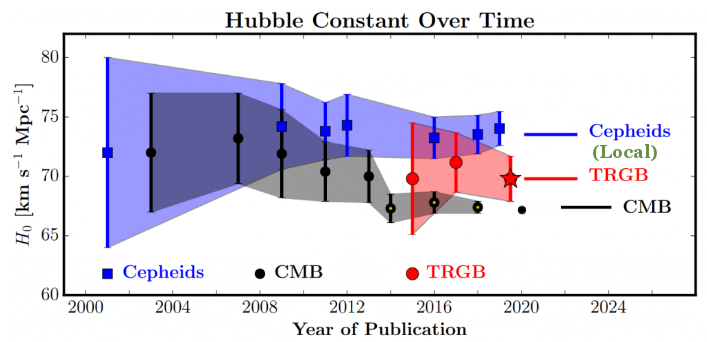 |
2018 Update on the "tension" - "Star Map Adds to Cosmic Confusion" 2019 Update on the "tension" - The 2019 TRGB data produce a Hubble constant H0 ~ 70 (km/sec)/Mpc which sits right at the middle between the contentious measurements from local Cepheids and the faraway CMB (see Figure 11t, and New Measure of Hubble Constant"). |
|
Figure 11t Hubble Constant, 2019 [view large image] |
 |
 |
The grand finale for CMB observation occurred on July 17, 2018 when the Planck Collaboration released to the public a new and improved version of the data acquired by the Planck satellite. Among other cosmic parameters (see "Planck Data, 2018"), the Hubble constant remains little change at a value of 67.4 km/sec-Mpc (Figure 11u) corresponding to 13.8 billion years for the age of the universe (see formula in Figure 11v) with  M = 0.317, and M = 0.317, and   = 0.683. Thus the tension is un-resolved by this final measurement (funding for another CMB satellite is unlikely). It remains the biggest controversy in the modern view of the Universe. Note that although the expansion = 0.683. Thus the tension is un-resolved by this final measurement (funding for another CMB satellite is unlikely). It remains the biggest controversy in the modern view of the Universe. Note that although the expansion
|
Figure 11u Hubble Constant, 2018 + 2020 [view large image] |
Figure 11v Age of the Universe, 2018 |
rate has a problem, the age of the universe as derived by WMAP and Planck turns out to be rather consistent, thank to the slightly different values of the density parameters. |
 |
 |
In July 2020, the Atacama Cosmology Telescope (Figure 11w) collaboration submitted 2 CMB research papers for publication. From the observed CMB map (Figure 11x), it calculates a value of H0 = 67.6  1.1 km/s-Mpc in very close agreement with Planck's H0 = 67.9 1.1 km/s-Mpc in very close agreement with Planck's H0 = 67.9  1.5 km/s-Mpc. Indeed its derived cosmic parameters are in agreements with CMB measurements by WMAP and Planck as a group; but the tension with the "local" measurements remains un-resolved. It is suggested that perhaps 1.5 km/s-Mpc. Indeed its derived cosmic parameters are in agreements with CMB measurements by WMAP and Planck as a group; but the tension with the "local" measurements remains un-resolved. It is suggested that perhaps
|
Figure 11w Atacama Cosmology Telescope [view large image] |
Figure 11x ACT-CMB, 2020 |
there's something wrong with the  CDM cosmological model. CDM cosmological model.See "Mystery over Universe’s expansion deepens with fresh data" by Nature, 23 July 2020. See the September 2021 H0 = 71 (km/sec)/Mpc via EDE. |
 |
In 2024, there were 2 publications (see "Could JWST solve cosmology’s big mystery?" + "The biggest mysteries") on the Hubble constant using the same standard candles (Cepheid, TRGB, and Carbon Stars) from JWST observations. The two results are at odd with 73 vs 69.1 km/sec-Mpc respectively (see Figure 11y). The discrepancy could cause by the fewer data (than by Hubble Space Telescope), choice of Density Parameters, or theoretical modeling. Anyway, the tension is still around at this point. | |
Figure 11y Hubble Constant, 2024 [view large image] |
 c2 = E/V, and c2d
c2 = E/V, and c2d = dE/V - (
= dE/V - ( c2/V)dV;
c2/V)dV; R3 and dV = (3V/R)dR,
R3 and dV = (3V/R)dR,
 + 3[(dR/dt)/R](
+ 3[(dR/dt)/R]( + p/c2) = 0, or
+ p/c2) = 0, or 
 = -3H(1+w)
= -3H(1+w) , where H = (dR/dt)/R.
, where H = (dR/dt)/R.