Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Relativity, Cosmology, and Time

Cosmological Constant and de Sitter Universe

It is found lately that the cosmic expansion may be accelerating. An additional term with the cosmological constant is added to the gravitational equation (18a) as a possible candidate for the dark energy to drive the acceleration. It was originally introduced by Einstein to address the failure of constructing a static universe. Thus Eq.(18a) becomes:

Cosmological constant (dR/dt)2 + kc2 = 8GR2 / 3 + R2 c2 / 3
where R(t) is the scale factor related to the size of the universe, the cosmological constant. It can be expressed in term of the corresponding density by the formula = 8G / c2. Assuming a flat universe, current observations of distance supernovae, the cosmic microwave background radiation, and the dynamics of galaxies together favor a value of = 0.7 c, the numeric value for is about 1.3x10-56 cm-2. Past attempts to identify the cosmological constant with the vacuum energy of the various quantum fields was not very successful. See "Vacuum Energy Density" for a 2015 update. The effect of the cosmological constant on the cosmic expansion is summarized in Figure 10h.

Figure 10h Cosmological Constant [view large image]

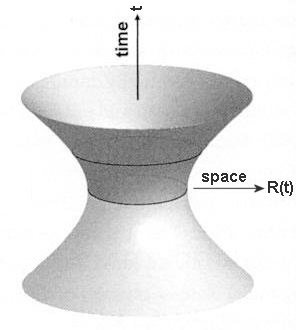
The de Sitter universe is devoid of matter energy containing only vacuum energy. It follows that Eq.(20a) is simplified to:

(dR/dt)2 + kc2 = R2 c2 / 3     or     (dR/cdt)2 - R2 / 3 = -k ---------- (20b).

For k = 0, the solution is: R(t) = R0 eHt
de Sitter Universe where H = (/3)1/2c = (dR/dt)/R is the Hubble constant, and R0 is a constant.. This solution shows the weird property of a constant matter-energy density , i.e., vacuum energy is continuously being created to fill up the void in the wake of the expansion. The idea is similar to the steady state universe, which requires the continuous creation of matter. Since the event horizon is dh = c / H = 1 / (/3)1/2 = constant; therefore, like the earth's horizon, the de Sitter horizon can never be reached - it is always a finite distance away. The de Sitter universe with k = 0 starts at t - from a singularity. It reaches a size of Ro at t = 0, and expands to infinity as t +. Alternatively, Ro at t = 0 can be taken as the initial condition. The universe then can either grow or decay exponentially. Note that Eq.(20b) is time reversal invariant. For some reason, this universe chose to grow exponentially in the positive time direction.

Figure 10i de Sitter Universe with k = +1
[view large image]

 For k = +1, R(t) = R0 cosh(Ht) R0 eH|t| as t .
Figure 10i depicts a de Sitter universe with k = +1 from t - to t +. It shrinks to a minimum size of (c/H) at t = 0.

For k = -1, R(t) = R0 sinh(Ht) (R0/2) eHt as t . Its size shrinks to zero at t = 0. There is no solution for negative t as R also becomes negative.

All de Sitter universes expand forever exponentially. Such behaviour is similar to the situation at the very beginning and very end of our universe, either when energy matter had not been created or they have been diluted so much at the end.

The anti-de Sitter (AdS) universe is also described by Eq.(20b) except that is now negative.

For k = -1, R(t) = R0 sin(Ht).

where H = (-/3)1/2c. There is no solution for k = 0, and k = +1. Since a negative implies attraction, the AdS undergoes a cycle of expansion and contraction with a time scale of /H (see Figure 10h).

The simple de Sitter, anti-de Sitter models suggest that for large positive , everything flies apart so quickly that there is no chance for matter to assemble itself into sturctures like galaxies, stars, planets, atoms or even nuclei. On the other hand, with large negative , the expanding universe quickly turns around and terminates the evolution of life before it can arrive at the present state. The estimated value of about 0.7x10-29 gm/cm3 seems to be fine tuned for the existence of life. Nobody is able to find an explanation for such coincidence yet.

The steady state universe requires continuous creation of matter in order to keep the expanding universe uniform everywhere and anytime. The refutation of the theory came with the observation that quasars were found only at large distances. The discovery of microwave background radiation, which indicates a much denser state further back at the time of Big Bang, finally ruled it out completely.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu

.