Relativity, Cosmology, and Time

Five Dimensional Space-time

It is found that when 4-dimensional theory is formulated in a 5-dimensional space-time, novel features emerge as the theory is reduced back to 4-D. The Kaluza-Klein theory introduced in the 1920s is the most famous example, which unifies the theories of gravitation and electromagnetism. The technique of compactification to hide the extra-dimension is now used extensively in the superstring theory. It is from the process of compactification that produces various particle properties.

Figure 10r 5-D Space-time [view large image]

If experimenters discover new heavy particles with the same charges as familiar ones and masses that are similar to one another, those particles will be strong evidence of extra dimensions. If such particles also occur at regular intervals of mass, it would very likely mean that a simple curled-up dimension has been discovered. But more complicated extra-dimensional geometries will yield more complicated patterns of masses. If enough such particles are discovered, the KK particles would then reveal not only the existence of extra dimensions, but also the their sizes and shapes. Since no KK particle has been detected so far, it seems to indicate that the size of the curled-up dimension could be very small.

Figure 10s KK Tower [view large image]

In unit of ev, the mass of the KK tower Mn = (n/R) x 1.2 x 10-4 ev. Thus, the new LHC collider (to be operational in 2007) with available energy up to 14 Tev can probe the curled-up dimension down to the size of about 10-17 cm.

Several conclusions can be drawn from this simple example:


• The compactification of a dimension creates a quantization of the momentum corresponding to the compactified coordinate. The momentum is labeled by integers.
• The mass spectrum in the space-time dimensions that are not compactified is shifted by an effective mass term coming from the compactified dimension.
• The radius of the compactified dimension can be totally arbitrary as long as it can hide that dimension from observation.
• In general the components with from 1 to 4 will recover the original theory with additional term. The = 0 component will generate some kind of physical property. In some other theories when there are cross terms between the = 1, ...,4 and the = 0 components, other theories will emerge from the reduction.

Some comments on the Kaluza-Klein theory:


• The extra dimension is not curl-up and satifies the periodic condition. It is proposed instead that g_ik should not depend on x₀, which implies g₀₀ is a constant.
• The reduction of the (, ) (from 1 to 4), (0, ), and (0, 0) components of the curvature tensor respectively generates the gravitational, electromagnetic, and scalar fields.
• The reduced equations for gravity is similar to the original gravitational field equations in Eq.(12a). The additional term is the electromagnetic stress-energy tensor, and k ~ g₀₀ is the gravitational constant.
• The electromagnetic equations are modified by a factor of (-g)^1/2, where g is the determinant formed from g_ik.
  F = g_0, - g_0, is the electromagnetic anti-symmetric tensor defined in the original equations. Indices separated by a comma will denote differentiation with respect to the corresponding coordinate.
• The massless scalar field is called radion or dilaton. It can be interpreted as the length or size of the fifth dimension as a function of the usual four dimensions of space-time. In string theory, the dilaton always appears together with gravity.
• The equation of motion in the reduced 4-D space-time takes the form:
  
  
  
  where ₀ is the mass density. The interaction terms involve the gravitational field interacting with the energy-momentum density, and the electromagnetic field interacting with the charge-current density.

Nowadays, we know that electromagnetism and gravity are far from being the whole story. A satisfactory unified theory must accommodate a good deal more like the weak and strong interactions. In fact, five dimensions are not enough; we might just manage with ten (such as in the string theory). The Kaluza-Klein method has been generalized to Yang-Mills theory in (4+N)-dimensional spac-time. If supersymmetry is added to the formulation, the new components of the super curvature tensor emerge as

Figure 10t Supergravity [view large image]

quarks and leptons. Such formulism is called supergravity. The decomposition is illustrated in a much simplified form in Figure 10t.

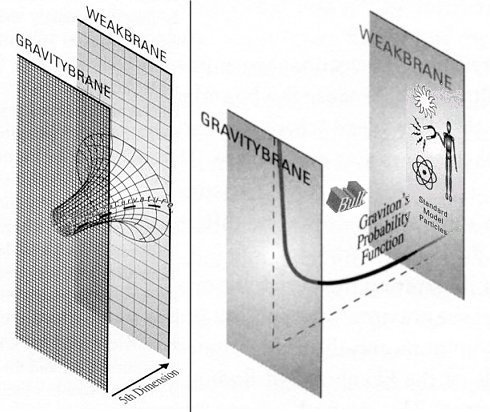An interesting application of warped 5th dimension has been developed by Lisa Randall. In this model, the 5th dimension is located in between two 3-D branes. It is found that the extra dimension is severely warped in the form of anti de Sitter space with positive curvature by the presence of positive energy Gravitybrane and negative energy Weakbrane even though the branes themselves are completely flat (see Figure 10ua). The strength of gravity depends on the position of the 5th dimension. As shown in Figure 10ua (in term of graviton's probability function), it can be very strong on the Gravitybrane but becomes feeble on the Weakbrane where all the forces and particles in the Standard Model are confined. Only the gravitons can move anywhere in the branes and in the bulk. This model

Figure 10ua Warped 5-D Space-time [view large image]

explains why gravity is weak in our world although it can be very strong in another brane. As the number of gravitons decreases exponentially, the separation between the two branes in the order of a few Planck length is sufficient to explain the hierarchy problem of huge

difference in mass between the Planck scale mp=(c/G)1/2 and the Electro-weak scale. If the mass of these two scales is similar at the Gravitybrane, then the Planck mass on the Weakbrane would be boosted up by a factor of 1016 as the gravitational constant G is correspondingly reduced when the two branes are separated by 32 curvature units away. It is suggested that LHC could be used to verify this theory by detecting the decay products,

Figure 10ub KK Particle Decay Mode

e.g., an electron/positron pair, from the predicted KK graviton (Figure 10ub). The model of Gravity Leak to Extra-dimensions provides another prediction on KK particle production.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu