
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
were developed in the form of calendars. The Egyptian pioneers first divided a day into 24 units. Other calendars were linked to religion and the need to predict days of ritual significance, such as the summer solstice. All calendars had to resolve the incommensurate cycles of days, lunations and solar years, usually by intercalating extra days or months at regular intervals. The Julian calendar was established at 46 BCE. The first mean of measuring daily time was probably the Egyptian sundail, dating from about 1500 BCE (Figure 11a). It was soon followed by the water clock or clepsydra and the sandglass or hourglass, in which time is measured by change in level of flowing water or sand. The earliest mechanical clocks containing movable parts were built about 700 years ago. It had no minute hand. In the beginning, time is cyclic, but it becomes |
Figure 11a Sundail |
linear when the cycles are added up together turning into history. |
 |
When Newton published the three natural laws in 1686, time is no longer confined to record the daily and yearly rhythms. It had become a mathematical entity - a parameter to keep track of motions in a fixed, infinite, unmoving space. Einstein changed this with his relativity theories, and once wrote, "Newton, forgive me." In the new theories, time is treated almost on the same footing as the spatial dimensions with some essential differences. Recently, theory in quantum gravity considers time and space to be discrete at Planck scale with a minimum temporal interval and spatial size of about 10 -43 sec and 10-33 cm respectively. At this scale, they are useless as framework for the motion of other objects. It is suggested that time and space are the active participants in the dynamics of this world. |
Figure 11b Newton [view large image] |
 |
While space and time can emerge in mathematical formula or graph in symbol or curve (Figure 11c,a), the five senses of human fail to perceive space and time directly. We recognize space through its representation by some features such as a house, a hill, or a galaxy, ... (Figure 11c,b) and similarly, the representation of time has to be a sequence of events (Figure 11c,c). Scholars over the eon have lamented about the difficulty of defining time. A lot of confusion could be mistaken representation of time as the "TIME" itself. Thus, instead of trying to define time or provide an answer to the philosophical question of "What is time?", some of the characteristics and/or interpretations of time-representation are listed in the followings : |
Figure 11c Representations of Space, Time [view large image] |
 |
The arrow of time often invokes an image of time flying into one direction. In reality, time is ticking at its own pace; only the underlying representation is moving in that direction as shown by the entropy evolution in Figure 11e below. In this instance, the universe has so many different configurations (in terms of position and velocity) for the objects to occupy; there is very little chance that they will return to the more confined pattern once the holding force is removed. The situation is quite different for a closed system of only one or two particles, it is more likely for them to return to the previous configuration. Thus, the arrow is applicable mostly to an emsemble of many objects. |
Figure 11d Arrows of Time |
 |
|
Figure 11e Thermodynamic Arrow of Time [view large image] |
 |
|
Figure 11f Cosmic Expansion |
expansion. Figure 11f illustrates one more time that it is the ever increasing cosmic expansion that causes the apparent flow of time in one direction. |
 |
|
Figure 11g Einstein and Friend |
integrated into an estimate of how much time has passed - producing the subjective time. It is suggested that such subjective time can be manipulated by brain chemistry, in particular the dopamine (one kind of neurotransmitters that controls arousal levels). It is known that patients with disorders in its secretion, |
 |
The asymmetry between past and future has two aspects. On the one hand, we know events happened in the past by memory recall, history books, fossil records, and astronomical observations etc., but we know nothing about the future. The direction of time in which we remember the past and not the future is referred to as the psychological arrow of time (Figure 11g). On the other hand, we can only move forward into the future and can never go backward to the past physically. This kind of asymmetry is related to the principle of cause and effect (causality), which is an important concept in physical theories. For example, the notion that events can be ordered into causes and effects is necessary to prevent contradictions such as the grandfather paradox, which asks what happens if a time-traveller kills his own grandfather before he ever meets his grandmother. Within special relativity, causality can be preserved by forbidding information from traveling faster than the speed of light - the worldline is not allowed to loop back to the past. It is strongly suspected that general relativity also preserves causality and forbids agents from changing the past, despite the possibility of developing a closed time-like curve. In term of the huge number of possible configurations, the asymmetry can be explained by the very low probability for reproduction of the past events; by the same token we cannot predict what will be the next configurations. Regardless, the idea of using time machine to visit the past is still a hot topic in science fictions. Figure 11h shows a fictitious time machine. |
Figure 11h Time Machine |
  |
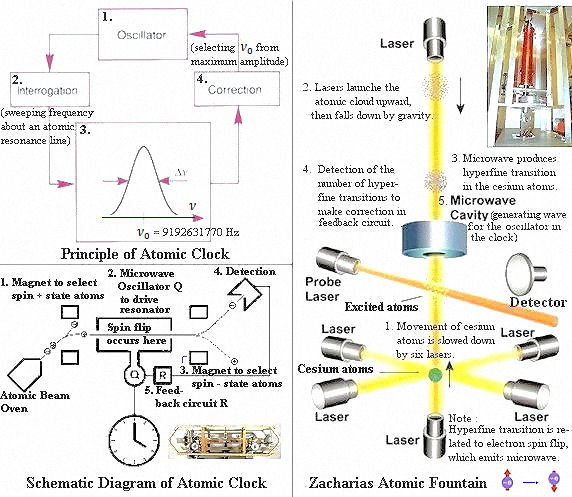 |
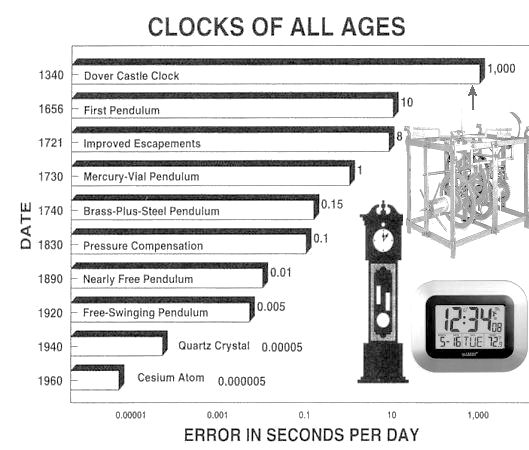
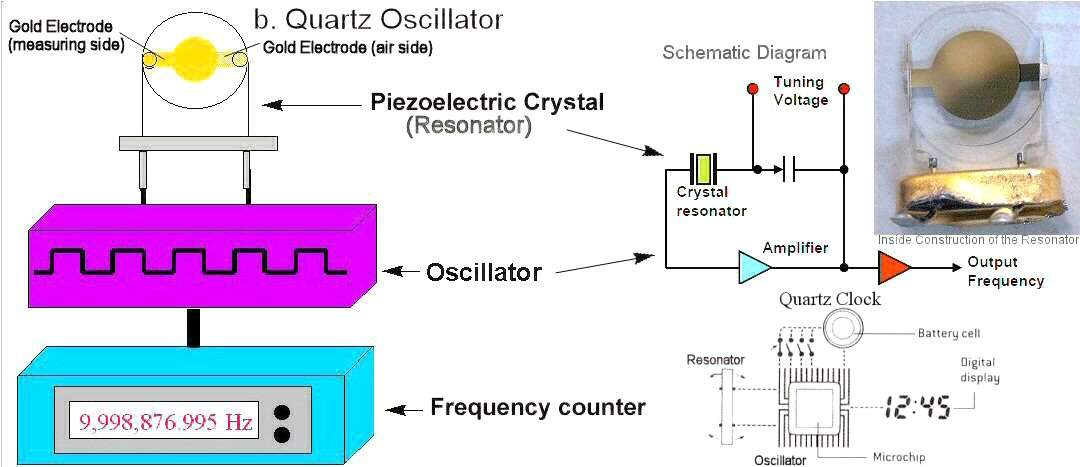
Modern quartz clocks use the piezo-electric properties of the quartz crystal, which vibrates at a specific frequency when placed in an alternating electric current circuit. The induced "crystal current" (the oscillator) is amplified and used to operate an LED display or electrically actuated hands (see Figure 12b). The circuit advances the time display by 1 second for every 9,998,876,995 oscillations (Hz). Atomic clocks use the frequency of atomic emission to regulate a quartz crystal clock (see Figure 13). One second is now defined as 9,192,631,770 oscillation (the frequency of the atomic line emission) associated with the microwave from the hyperfine transition of cesium atoms. All types of design depend on the tuning of the microwave cavity |
Figure 12 a, b Clocks [view large image a, b] |
Figure 13 Atomic Clock |
to find the frequency, which induces the maximum number of transitions between the hyperfine states. This is used as reference to measure error in the output frequency (to the clock). Any deviation |
 |
In the next generation atomic clock, the microwave cavity is replaced by the frequency comb, which generates a train of million laser pulses each one with a different frequency (in optical range). The frequency comb is used to probe a lattice of atoms cooled to microKelvin temperature. The sweep produced a profile (the bell curve in Figure 14a). Due correction is made according to the difference between the frequencies at the peak (corresponding to the most intense signal induced by one of the comb frequencies) and the actual output to the clock. It is |
Figure 14a Atomic Clock, Next Generation [view large image] |
claimed that this new model is ten times more accurate than the conventional atomic clock. One of the problems is synchronization, which is more difficult to achieve than the microwave signals from the older model. |
 c. They are the consequence of trying to reconcile the following two equations :
c. They are the consequence of trying to reconcile the following two equations : |
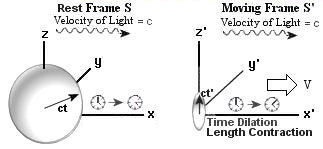 |
x2 + y2 + z2 = c2 t2 or x2 + y2 + z2 - c2 t2 = 0 (for an observer in the S frame) ---------- (1) x'2 + y'2 + z'2 = c2 t'2 or x'2 + y'2 + z'2 - c2 t'2 = 0 (for an observer in the S' frame) ---------- (2) |
Figure 14b Classical Mechanics [view large image] |
Figure 14c Special Relativity [view large image] |
Thus, the simple Galilean transformation between inertial frames : x' = x - Vt, is replaced by the Lorentz transformations (Figures 14b,c): |
 |
 c, or else it becomes an imaginary variable which has no place in the present context. Violation of this rule creates non-senses in other variables such as mass. The rule also makes sure that cause goes before effect, i.e., the light curve cannot be bend backward toward the past (see Figure 14d). c, or else it becomes an imaginary variable which has no place in the present context. Violation of this rule creates non-senses in other variables such as mass. The rule also makes sure that cause goes before effect, i.e., the light curve cannot be bend backward toward the past (see Figure 14d).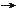 c, and 1/(1 - V2/c2)1/2 c, and 1/(1 - V2/c2)1/2   . . |
Figure 14d Light Cone |
 |
In general relativity, time or actually i ct attains an equal footing with the spatial coordinates and denoted as x4 = i ct. Space and time are merged together called space-time. For example, the space-time interval for a particle is expressed in the form : -ds2 = g  dx dx dx dx where where  and and  are the indices running from 1 to 4. In particular, the space-time interval for a point mass M in spherical coordinates is : are the indices running from 1 to 4. In particular, the space-time interval for a point mass M in spherical coordinates is :-ds2 = -(1 - 2GM/c2r) c2dt2 + dr2 / (1 - 2GM/c2r) + r2 ( d  2+sin2 2+sin2 d d 2) ---------- (4) 2) ---------- (4)in which g44 = (1 - 2GM/c2r), g11 = 1/(1 - 2GM/c2r), g22 = r2, g33 = r2 sin2  . .For the case when r = 2GM/c2, g44 = 0, while g11  . This is the Schwarzschild radius or event horizon . This is the Schwarzschild radius or event horizon
|
Figure 14e Black Hole |
of a black hole (Figure 14e) for which it is often dubbed as space-time warp. In fact, space-time behaves as usual, only the metric tensor g11 becomes infinity and nobody know what's beyond the horizon. |
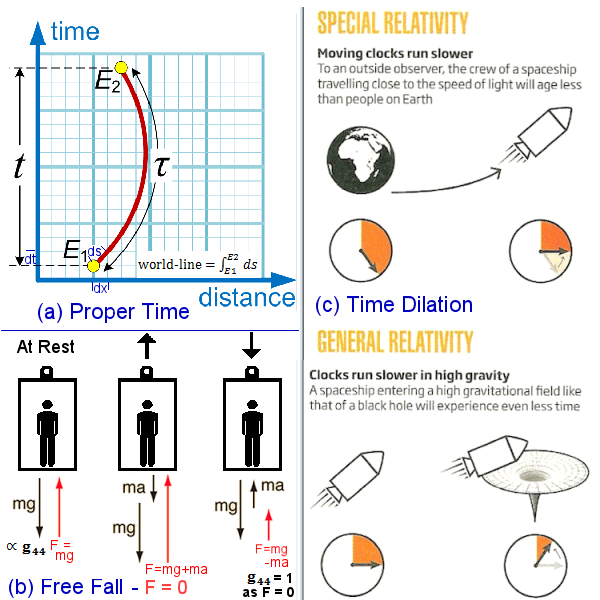 |
On the other hand, time dilation (Figure 15,c) may be a kind of time warp from the view point of the proper time  , which is defined as the time moving together with the observer and hence the spatial derivatives vanish in this particular choice of frame, i.e., ds2 = c2d , which is defined as the time moving together with the observer and hence the spatial derivatives vanish in this particular choice of frame, i.e., ds2 = c2d 2 (Figure 15,a); while for another observer ds2 = c2dt2[1-(V/c)2]. Since the space-time interval ds is an invariant under the Lorentz transformation between different inertia frames, the proper time d 2 (Figure 15,a); while for another observer ds2 = c2dt2[1-(V/c)2]. Since the space-time interval ds is an invariant under the Lorentz transformation between different inertia frames, the proper time d = dt[1-(V/c)2]1/2, which shows that proper time runs slower according to an outside observer and hence the twin paradox. = dt[1-(V/c)2]1/2, which shows that proper time runs slower according to an outside observer and hence the twin paradox.
In general relativity, the proper time would be the one associated with the free-fall frame where the supporting force F becomes zero (Figure 15,b). Thus, ds2 = c2d  2 ; while for a rest frame ds2 = g44c2dt2 . It follows that d 2 ; while for a rest frame ds2 = g44c2dt2 . It follows that d = (g44)1/2dt. For the case of running around a black hole horizon (g44)1/2 ~ (1 - 2GM/c2r)1/2, the proper time runs very slow according to an outside observer not plunging into the black hole. = (g44)1/2dt. For the case of running around a black hole horizon (g44)1/2 ~ (1 - 2GM/c2r)1/2, the proper time runs very slow according to an outside observer not plunging into the black hole.
|
Figure 15 Proper Time |
The proper time in cosmological expansion is d = R(t)dt, where R(t) is the scale factor. The corresponding space-time interval is : -ds2 = -c2dt2 + R(t)2 [dr2 + r2 (d = R(t)dt, where R(t) is the scale factor. The corresponding space-time interval is : -ds2 = -c2dt2 + R(t)2 [dr2 + r2 (d 2 + sin2 2 + sin2 d d 2)], where t is the co-moving time. 2)], where t is the co-moving time.
|
 0, i.e., it almost stopped ticking at the beginning of the universe according to an external observer, i.e., the spectral line is red shifted to infinity. BTW, this is the beginning of time according to the "Standard Cosmology". The latest data from observation of the CMBR yield an age of 13.8 billion years. Some cosmological models assert that there is no beginning of time (see "Cyclic Universe").
0, i.e., it almost stopped ticking at the beginning of the universe according to an external observer, i.e., the spectral line is red shifted to infinity. BTW, this is the beginning of time according to the "Standard Cosmology". The latest data from observation of the CMBR yield an age of 13.8 billion years. Some cosmological models assert that there is no beginning of time (see "Cyclic Universe").  E
E  t >
t >  , and in the commutative relation (Et - tE)
, and in the commutative relation (Et - tE) = i
= i
 . The uncertainty principle implies that the energy of the system is stationary (the eigen-energy) if
. The uncertainty principle implies that the energy of the system is stationary (the eigen-energy) if  t
t  ; on the other hand virtual particle with certain
; on the other hand virtual particle with certain
 |
mass-energy  E can pop up to its brief existence in finite E can pop up to its brief existence in finite  t allowed by the uncertainty. The eigenvalue solutions in Quantum Mechanics are very important in understanding the atomic and molecular structures, while the virtual particles would alter the dynamic of particle interactions (Figure 16a). The commutative relation requires E to be an operator in the form i t allowed by the uncertainty. The eigenvalue solutions in Quantum Mechanics are very important in understanding the atomic and molecular structures, while the virtual particles would alter the dynamic of particle interactions (Figure 16a). The commutative relation requires E to be an operator in the form i d/dt. d/dt.
|
Figure 16a Quantum Time [view large image] |
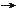 -t operation (designated by T). However, the observable universe does not show such symmetry, primarily due to the "second law of thermodynamics".
-t operation (designated by T). However, the observable universe does not show such symmetry, primarily due to the "second law of thermodynamics". |
|
Figure 16b Time Reversal, Symmetry and Violation [view large image] |
Figure 16b shows the time reversal invariance in physical law and quantum process with T represents the operation. It also portrays a sequence of time irreversible implosion. |
 |
Another kind of time transformation is the translation or adjustment of the clock by a certain amount. The following example shows in detail the conservation of energy if the dynamics of the system is invariant under time translation, i.e., from t to t0 + t. This is a simple case of a falling object of mass m under the gravity g at height h from the surface of the Earth (Figure 16c).
|
Figure 16c Conservation of Energy [view large image] |
 |
 |

|
Figure 16d Effective Theories [view large image] |
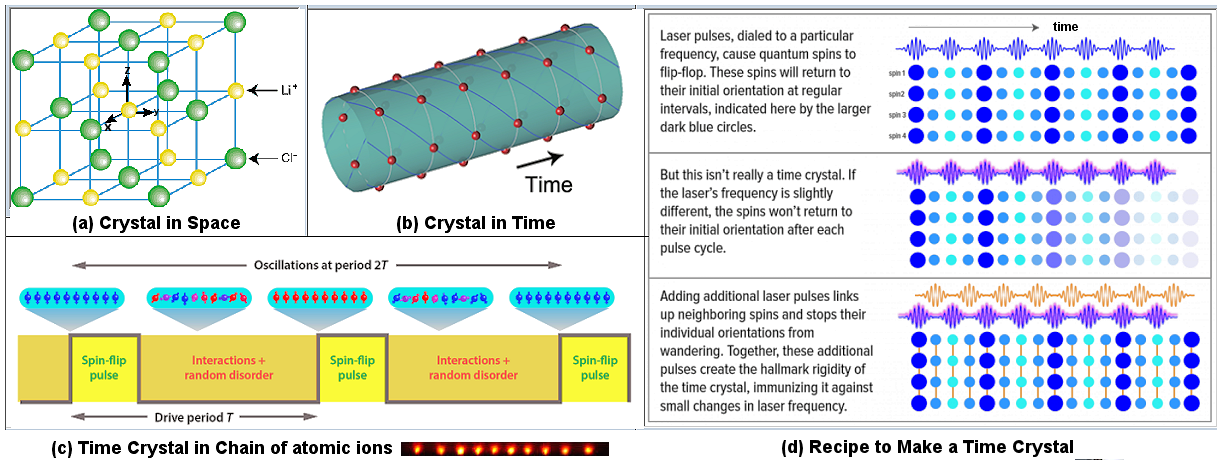 |
the continuous translational symmetry is replaced by the discrete translational symmetry (Figure 17d,a). It is suggested in 2012 that the continuous temporal symmetry could be broken similarly in time. The original idea envisioned a collection of objects repeating a certain pattern at regular interval (dubbed time crystal, Figure 17d,b). It would be in ground state and the motion would last forever. Subsequently, a theorem was derived in 2015 to show that such system is impossible to create in ground state and in equilibrium. |
Figure 17d Time Crystal [view large image] |
 |
|
Figure 17e Time Crystal in Dimond |
 |
The difference between time crystal and the spatial one is mainly on the interaction to hold the thing together. In time crystal it has to be infused from outside artificially and thus the structure collapses once the external support is removed or becomes ineffective by coupling with the environment. Depending on the interaction time  1, the lifetime of the time crystal can reach to about 60x10-6 sec as shown in Figure 17f. Anyway, this is a very simple example out of a host of new phases that exist in relatively unexplored out-of-equilibrium states. 1, the lifetime of the time crystal can reach to about 60x10-6 sec as shown in Figure 17f. Anyway, this is a very simple example out of a host of new phases that exist in relatively unexplored out-of-equilibrium states. |
Figure 17f Lifetime [view large image] |
It is suggested that the two spin orientations in time crystal can be used as the qubits in room temperature quantum computing. Other application includes detection in tiny changes of temperature and magnetic field. |
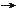 it'. This simple substitution is rather controversial in the community of theoretical physicists. Some argue that it is merely a mathematical trick, or a convenient tool devoid of any physical significance. Others suggest that imaginary time is the true physical quantity. Whatever its merit, imaginary time does provide an alternate computational technique and conceptional viewpoint as shown in the following examples (Note that imaginary and real are just mathematical terminologies in this context. It has nothing to do with the usual connotation of mental perspective.).
it'. This simple substitution is rather controversial in the community of theoretical physicists. Some argue that it is merely a mathematical trick, or a convenient tool devoid of any physical significance. Others suggest that imaginary time is the true physical quantity. Whatever its merit, imaginary time does provide an alternate computational technique and conceptional viewpoint as shown in the following examples (Note that imaginary and real are just mathematical terminologies in this context. It has nothing to do with the usual connotation of mental perspective.).

 |
Meanwhile, if the imaginary time is substituted into Eq.(10), it changes into a form familiar to Euclidean geometry: ds2 = dx2 + dy2 + dz2 + c2 dt'2 ---------- (7) While the real time in Eq.(10) restricts the time direction within the light cone, for the imaginary time there is no difference between the time direction and directions in space. Thus according to Hawking, it is possible for such space-time to be finite in extent and have no singularities that formed a boundary or edge. As shown in |
Figure 17a The "No Boundary" Proposal |
Figure 17a, space-time would be like the surface of the earth, only with two more dimensions. Such Euclidean sphere has zero points at the North and South Poles, but these points would not be any more singular than these Poles on earth. This is the "No Boundary" proposal, which not only avoids the singularity in space but also |
 |
universes. The sum over histories is actually performed backward in time from the current state of the universe such as three-dimensional and flat, then construct the set of all possible histories that would end up like ours (with variables such as inflation, big crunch, ...), and finally sum them up by assigning a weighting factor to each to produce the probability amplitude for the history of a certain universe (see Figure 17b). Although the answer matches observations (i.e., our universe is the most probable) and incur no singularity, many physicists argue that this is |
Figure 17b Sum over Histories [view large image] |
just giving up on the problem of explaining why our universe is the way it is - it is not, they say, science. |
 |
In an equally un-orthodox idea, the Schrodinger equation in quantum mechanics has been carried over to cosmology. The only difference being that its solutions, instead of describing the possible values of the position or momentum of a particle, represent the possible geometrical shapes of the Universe. Quantum effects are thus introduced into cosmology with such interpretation. This is called Wheeler-DeWitt equation: [ d2/dR2 - U(R) ]  = 0 ---------- (8) = 0 ---------- (8)where R is the scale factor, U is the "potential" (a function of R, the curvature, the cosmological |
Figure 17c Wave Function of the Universe |
constant, the densities of matter, and radiation), and  is the wave function of the universe, in which the particle position is replaced by the radius R for a multitude of universes. The analogy has been extended further by quantization of the Wheeler-DeWitt wave function leading to the is the wave function of the universe, in which the particle position is replaced by the radius R for a multitude of universes. The analogy has been extended further by quantization of the Wheeler-DeWitt wave function leading to the |
 |
Instead of playing with "no time", how about constructing theory with 2 dimensions of time? It was found long time ago that such theory leads to negative probability. Worse still, it admits the weird case of time travel backward as shown in Figure 19. Thus, the two-dimensional time gives every appearance of being a non-starter. However, it is shown in a research work in 2007 that the problems disappear if some kind of symmetry is imposed on position and momentum, and the theory involves one more spatial dimension, i.e., our 4-D space-time is generalized to 6-D space-time with 4 spatial dimensions and two time dimensions. It is suggested that the world we see around us is merely a "shadow" of a 6-D world. According to this idea, the standard model is just one shadow (projection) of this 6-D world. There are other shadows that include gravity, finally uniting it with the standard model. Although the effects of an extra time dimension are subtle, it is purported to be very real out there. For example, the problem associated with the axion (a not yet observed entity) can be resolved by the application of 2D-time physics without such hypothetical particle. |
Figure 19 Two Dimensional Time [view large image] |
 |
Another attempt to do away with time asserts that it is all an illusion. The thermal time hypothesis (Figure 20) suggests that a statistical effect gives rise to the "appearance" of time. Similar to temperature, which is the average of the momentum of each molecule, the same applies to the thermal time but including many more constituents such as space (which is expanding on the average). It predicts that the ratio of the observer's proper time to the thermal time is the surrounding temperature. A toy model has been constructed successfully from the CMBR data to explain the cosmic expansion as described by standard cosmology. It can also reproduce the temperature of a black hole associated with the Hawking radiation. The idea follows the rework of quantum mechanics without time. The evolution in time is replaced by the variation of correlations between things as mentioned above. Instead of "collapsing" the wave function of an electron, both the electron and the measuring device are described by a single wave function, and a single measurement of the entire set-up causes the collapse. |
Figure 20 Thermal Time |
It is anticipated that combining quantum mechanics with general relativity would become less daunting when it is rewritten in time-free form. The loop quantum theory is an example adopting such idea. |
 |
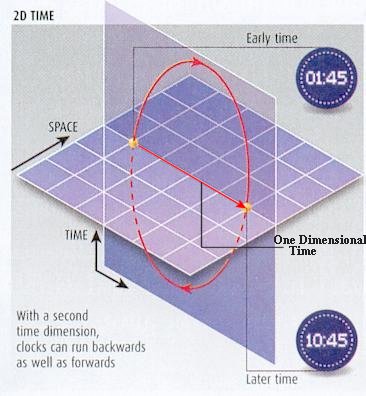
 |
Time was invented for the convenience of human to keep track of the changing NOWs. Note that the representation in phase space is background independent. The spatial coordinates x, y, z are absent in the picture, and so is the time. Essentially, this is the foundation of the so-called relational theory in which all that matters is the relationships or links between the events. It plays a crucial role in the formulation of loop quantum gravity, in which space and time are discrete quantities and evolve dynamically like the atoms. This idea was originated more than 100 years ago by Ernst Mach (honored by the Mach number = v/vsound) known as the Mach's Principle. The relationship between |
Figure 18a End of Time |
Figure 18b Configuration Space [view large image] |
objects in space is "relativity" in its original sense. Einstein's "relativity" is different in that it only "relates" space with time. |
 |
Then along came Julian Barbour who forewent an academic career to pursue Mach's idea. The task was highly unrewarding as no funding agencies would support such activity. He had to make a living by translating Russian text in scientific articles and lived in an idyllic farmhouse (Figure 18c, also see his Home Page) at South Newington. A March 2012 article in the Discover magazine presents the progress of his work on the subject since 1969. He is now a visiting professor at Oxford. In 2008 he won his first-ever official research grant and used the money to travel to conferences, as well as funding collaborators. Following is a summary of the progress: |
Figure 18c Julian Barbour and His Farmhouse |
See "timeless" published in 1999. |
 |
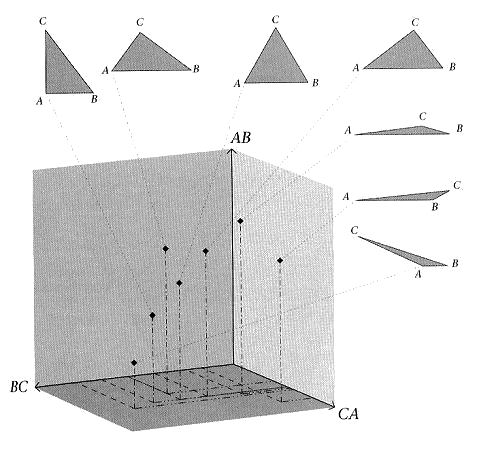
becomes rapidly unmanageable as the constituent number goes beyond three. Human perception of the configuration ranges from great detail to just a casual glance depending on the occassion. The ingenuity of the concept of time is to allow the different view points to link together in a sequence that is more useful than an individual event. There may be other way to view the configuration, but it would be a great mistake to do away with time. BTW, most living organisms may perceive only the NOWs, as they live from one moment to another. Most action is by instinct, some may learn from the past, a lot don't plan for the future. See an E. coli bacterium in action (Figure 18d). |
Figure 18d E. coli bacterium in Action [view large image] |