Relativity, Cosmology, and Time

Beginning of Time (2019 Version)

		Most models of early universe assume that time starts with the Big Bang. Study of a recent theory reveals that it may not be so. Time emerged gradually along with a sequence of events as illustrated in the followings. The novel features include a "rediscovery" of the Wheeler–DeWitt equation which suggests the disappearance of time in the formulation some 50 years ago. A simplified derivation for quantization of the Friedmann Equation (Matter-only) shows the same conclusion about timeless but also reveals a mechanism that can mimic the
Figure 01 Cosmic History and Planck Scale [view large image]	Figure 02 Interactions, 4-types [view large image]	phenomenon of inflation. Here's the mathematical formalism for such interpretation.

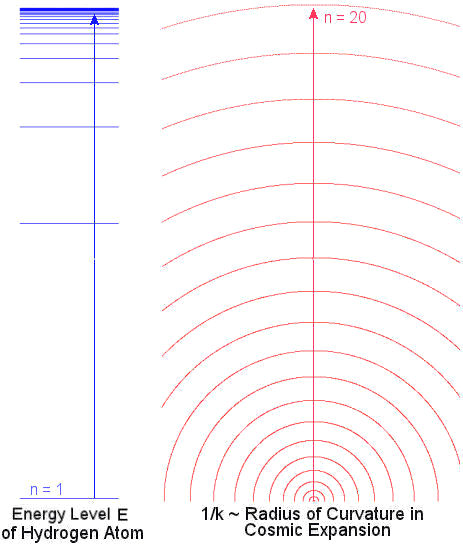Figure 03 H Atom Energy Level & Cosmic Curvature	See more cumbersome detail in the original derivation of "Quantization of the Friedmann Equation (Matter-only)" in 2011.

Some comments on the quantized Friedmann Equation :


1. Starting out from the gravitational field equation in General Relativity with relativistic invariance (which treats space and time on same footing), the cosmic expansion equation in Eq.(1a) singles out time as the sole variable so that the space-time unity is broken.


2. What's more, time is absent altogether in Eq.(2), which can be interpreted as representing a static configuration. It is similar to an isolated hydrogen atom just sitting there alone until a photon comes along to induce transition to other state. Similar occurrence could happen to the Planckian universe via interaction with graviton. However, the transition is to smaller spatial curvature k (see Eq.(3)) manifesting as "inflation" of space. The "inflation" terminates as the transition approaching the continuum, i.e., as n and k 0, that's when time began and standard (classical) cosmology took over.


3. The Planck length L_PL is the only parameter in the quantized Friedmann Equation. The form of mass/energy is not specified in
   Eq.(2). Actually, "mass" is a misnomer; it did not exist until some time later. Anyway, invoking E = Mc², the energy E can assume various form, it is not essential to pin-point which type(s) at this level. However, according to the conventional theory of inflation by Alan Guth, high energy particles were created near the end of the process.


4. The formulas in General Relativity is non-linear in the metric tensors ( ~ gravitational fields), this is the root of the problem for its quantization. The present scheme linearizes the Friedmann Equation and in the process enables the superposition of states - a key feature of quantum theory. For simplicity, it is assumed that the system is at its ground state with no superposition.


5. According to classical theory, this Planckian universe is a black hole since its radius L_PL < r_s = 2L_PL. It is not known what's the effect of qunatization on this black hole. A string theorist suggests that it turns into a fuzzball with no sharp event horizon (see "The Fuzzball Fix for a Black Hole Paradox")


6. When quantum fields are included into the vacuum of the Planckian universe (Figure 04), there would be virtual particles popping

   		up and vanishing briefly and incessantly according to the Uncertainty Principle tE (Figure 05). The t is an arbitrary time interval. There is lot of confusion about the meaning of time. Especially, about the time in quantum theory, which defines time as a variable different from space; while in general relativity, time is at the same level as space and is malleable (see "Quantum Time").
   Figure 04 Quantum Fields [view large image]	Figure 05 Virtual Particles [view large image]	Anyway, Quantum fluctuation has profound effect on the large structure such as super galactic cluster in the later epoch of the universe.

   
   
7. The Planckian energy density _PL = E_PL/[(4/3)(L_PL)³] = 10¹¹⁴ erg/cm³ persists during the quantum expansion. The mechanism could be similar to the virtual particle contribution to constant vacuum energy density, which seems to be a viable explanation in the very early universe (see Figure 06). However it is too large for standard cosmology. The problem could be with applying a quantum concept to classical physics in identifying this _PL to dark energy. The ad hoc merging does not always work.
   
   BTW, the standard theory of inflation proposes an inflaton field in the very early universe. The rapid expansion was driven by the constant vacuum energy density, which also has a value of 10¹¹⁴ erg/cm³ (see "Theory of Cosmic Inflation"). So ultimately, it is the constant energy density that drives the inflation in both cases (see a very simple explanation).


8. Since the quantum fields and virtual particles permeated throughout the space (Figures 04 and 05), there is no need to devise a mechanism for attaining a homogeneous and isotropic state.


9. According to the Holographic Principle, the black hole entropy is given by :
   S = (k_Bln2)[(R_Sh)²/(L_Pl)²],
   where R_Sh is the radius of the event horizon and L_Pl the basic unit in Planck length. As shown earlier, at the very beginning of the universe R_Sh = 2L_Pl, so that the entropy S = 4(k_Bln2) ~ 4k_B. This is the lowest amount of entropy at the beginning of the universe. It resolves the astronomical problem about the origin of low cosmic entropy. BTW, the cosmic entropy for today is about 10¹⁰³ k_B according to Ethan Siegel. This amount can be estimated from the average galactic R_Sh of about 10¹³ cm and the number of galaxies in present day of ~ 2x10¹².    About S ~ 10⁹⁶ k_B (for ~ 10¹¹² erg/cm³, T ~ 5x10³⁰ K, and V ~ 1 cm³) was infused during the "inflation" as shown in Figure 06. It has been increased ever since as the universe expands.


10. The temperature of black hole can be derived from the Hawking's radiation :
    T = [(E_Pl)²/Mc²]/8k_B,
    where M is the mass of the black hole. For black hole with the Planck mass T = E_Pl/8k_B = 5x10³⁰ K = 4x10¹⁷ Gev (see "A History of Cosmic Expansion" for comparison).


11. As mentioned earlier, time did not exist in the earliest era of cosmic expansion. For comparison purpose, the evaporation time of black hole is given by the formula (see another "Hawking's Radiation") :
    t_ev = 2x10⁶⁷(M/M_sun)³ years.
    which yields t_ev ~ 2.5x10^-42 sec for black hole with Planck mass (see "A History of Cosmic Expansion" for comparison).


12. The end of inflation as n marks the transition from quantum to classical cosmological model, which involves time (see Eq. (1)). This boundary is the "new" absolute zero time (Figure 01). It shifts the conventional cosmic time scale up by an negligible amount ~ 10^-33 sec. This instance could be associated with the appearance of particles, the emergence of strong interaction, and chiral symmetry breaking (Figure 02, also see "Naturalness, Chiral Symmetry, and Spontaneous Chiral Symmetry Breaking").


13. There is a discontinuity in time at the moment of transition. Time progresses forward only, there is no backward time at that point. Thus, time symmetry is violated at this point. Since charge and particle numbers also emerge at this moment (from zero to something), charge symmetry is also violated. Then the cardinal rule of CPT invariance in Quantum Field Theory is violated as each one is broken at that moment.

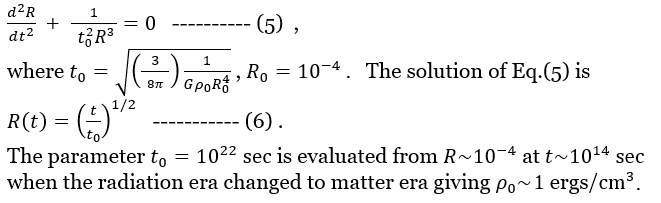
Figure 06 Energy Density Evolution [view large image]	Figure 07 Cosmic History, Very Early	Figure 06 shows the evaluation of the t0 and 0 parameters at the recombination point, while Figure 07 is a rough sketch for the evolution of the scale factor in very early universe.

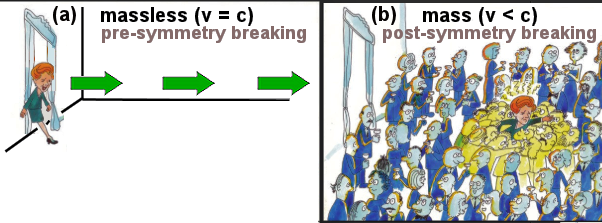		The same sketch also shows a very brief period of the order 10-10 sec when all the particles are massless. The Standard Model (SM) of elementary particles dictates that before the so-called "Electro-weak Symmetry Breaking", the Higgs field existed in false vacuum and could not interact with other particles making them massless (Figure 08,a) and all of them move at the speed of light (Figure 09,a).
Figure 08 SM, Parameters	Figure 09 Mass, Origin of [view large image]	See "Largranian for WS Model of SM", WS stands for Weinberg-Salam - two of the 1979 Nobel prize recipients for formulating the Stand Model. The third one is SG, who produced the QCD.

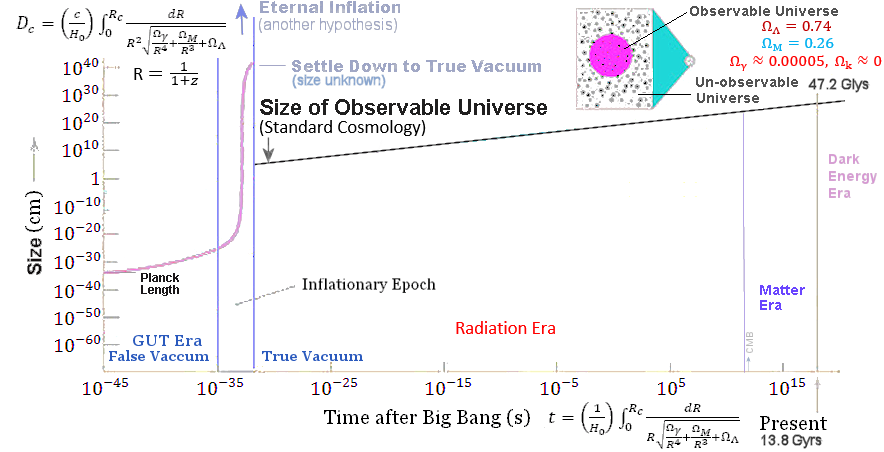BTW, As shown in Figure 08, this is also the point when the electro-weak interaction separated into the weak (with massive mediating bosons - making the force short range) and electromagnetic (with the massless photon - producing long range force) interactions. The size of the universe at t ~ 10-32 sec is R(t)x(size at current epoch) ~ 10-27x1028 cm = 10 cm. This is actually the size of observable horizon such as the one shown in Figure 07. The inflation could go beyond to the un-observable part as illustrated in Figure 10.

Figure 10 Cosmic Expansion [view large image]

In special relativity, the space-time interval ds is an invariance under the Lorentz transformation with ds2 = c2dt2 - (dx2 + dy2 + dz2). Since ds 0 for light wave as demanded by the theory, dt2 = (dx2 + dy2 + dz2)/c2 which shows that time is not an independent variable, it is proportional to the distance before the electro-weak transition. The proper time is defined by the clock sitting at x = y = z = 0, or ds cd = cdt. For an external observer moving with a relative velocity v, d = dt[1-(v/c)2]1/2 (Figure 11). Since v = c for all particles in that period, hence cd ds 0 as defined previously.

Figure 11 Inertial Frames

Accordingly, time can be defined as the rate of change R (for anything), e.g., on a particle's position R = dx/dt; beforce the electro-weak symmetry breaking, R = c; R c afterward depending on the interaction between the particle and Higgs. Such R is usually referred to as velocity v, the closely related entity is the linear momentum mv.

Back to "Ideas about Time".