Superstring Theory

Quantization

The Gupta-Bleuler quantization of the string requires the identification of the canonical momentum conjugate to X, i.e., P, which is defined as:

(which is defined as the integrand in Eq.(1)).

The spectrum of states is calculated from the Hamiltonian:

---------- (16)

For a closed string it takes the form:

---------- (17)

For an open string:

---------- (18)

This Hamiltonian is the simplest possible one for an extended object. While the last term is the energy for the center-of-mass, the sum is over an infinite set of independent harmonic oscillators, which is basically uncoupled from each other. This form admits simple products of the Fock spaces of all possible harmonic oscillators as its eigenstates:

---------- (19)

with the vacuum state defined by the annihilation operators: ---------- (20)
Each term in the sum in Eqs.(17) and (18) is similar to the number operator in quantum field theory. Eq.(15) shows that the norm for the time-like component is negative, i.e.,

---------- (21)

which is called ghost. This kind of negative probability is unacceptable in physical theory. Elimination of ghost states is possible by choosing the "light cone gauge", which defines two new coordinates according to the transformations:

X⁺ = ( X⁰ + X^D-1), X^- = ( X⁰ - X^D-1) ---------- (22a)

In this form, X⁺ can be chosen to describe the motion of the center-of-mass only; while X^- can be expressed in terms of the transverse degrees of freedom with

= 1, ..., D-2. There is no more time component and thus no more ghost states. In the light cone gauge the energy-momentum tensor can be defined as T₊₊ = ( T₀₀ + T₀₁) / 2, and T_-- = ( T₀₀ - T₀₁) / 2. The commutative relation for T₊₊ has the form:

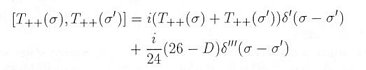---------- (22b)

In order to define the physical state properly, the second term on the righ-hand side of Eq.(22b) arised from an anomaly (an anomaly is the failure of a classical symmetry to survive the process of quantization and regularization) has to be removed. Thus, the dimension of the coordinate system has to be twenty six, i.e., D = 26. The constraint equations in Eq.(3) can now be written as: T₊₊ = T_-- = 0. Classically, these constraints can be implemented without much difficulty. However, quantum mechanically it is not possible to impose the conditions without inconsistency. It may be formulated in terms of the Fourier components of T₊₊ and T_-- as the conditions for the physical state |

>. Since the mass square M² = pp, the constraint in Eq.(3) yields the following formula for the closed string after integrating over

from 0 to

and evaluating at

= 0:

---------- (22c)

where the index i = 1, ..., D-2, and a is a formally infinite constant arising from the commutators. It is now regularized to be 1. For the open string:

---------- (22d)

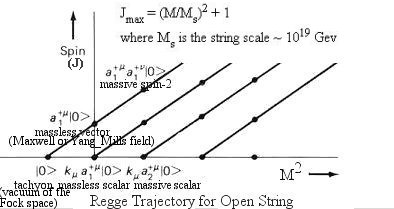		It was found in the 1960s that the spin (or angular momentum) of a family of resonances (short-lived elementary particles) is related to the square of mass by a simple line on a graph, which is known as Regge trajectory. Figures 03a and 03b show the theoretical derivation of such relationship for a few low-lying string states of the closed and open strings respectively.
Figure 03a Regge Trajectories, closed string [view large image]	Figure 03b Regge Trajectories, open string [view large image]

Considering the

_n⁺'s, or a_n⁺'s (

= n^1/2a) as components of vector, then following the rule of tensor calculus, the "outer product" such as a⁺a⁺ is a tensor of rank 2. Conversely, the "inner product" (contraction) of two vectors such as ka⁺ lowers the rank 1 vectors to a scalar with rank 0. All the bosonic spin states can be constructed from this scheme in accordance with Eq.(19). The value of M² corresponding to the various string states are computed from either Eq.(22c) or (22d) with the pairs of

's acting as number operator. Table 01 shows many of the low-lying string states as depicted in
Figures 03a and 03b.

String Type	Spin	M²	Name
Open	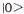0	-2	vacuum with tachyon
Open	0	0	massless scalar
Open	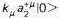0	2	massive scalar
Open	1	0	massless vector (photon)
Open	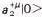1	2	massive vector
Open	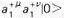2	2	massive spine-2
Closed	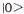0	-8	vacuum with tachyon
Closed	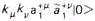0	0	massless scalar
Closed	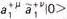2	0	massless spin-2 (graviton)

Table 01 Low-lying Bosonic String States

Figure 03a displays a massless spin-2 particle in the spectrum of the closed string. This graviton-like particle was a great embarrassement when the string was first being developed as a model of hadrons. Now it is interpreted as a natural incorporation of gravity with the quantum theory of string. When the mathematics of this harmonic mode is worked out, it is found that the equations governing the large-scale behavior of a collection of gravitons are exactly those of general relativity. Thus, the superstring theory can be considered to give a fundamental generalization of general relativity. But the concepts behind this generalization remain largely mysterious.

Eqs. (19) and (22c,d) in the quantized theory of string show that each vibrational mode corresponds to a particle with distinct spin and mass. Unfortunately, as shown in Table 01 only the massless states have counterparts of particles in the real world (observed in the case of photon or not-yet-observed in the case of graviton), other states are either unreal (such as the tachyon) or too heavy in the range of 10¹⁹ Gev and beyond.

See an "Introduction to Superstring Theory".