Superstring Theory
Supersymmetry and Superstring
The superstring theory is based on the introduction of a world sheet super-symmetry that relates the space-time coordinates
X (
( ,
, ) to a fermionic partners
) to a fermionic partners 
 (
( ,
, ), which are two-component world sheet spinors. The action S consists of three parts:
), which are two-component world sheet spinors. The action S consists of three parts:
S = S0 + S1 + S2 ---------- (23)
In this equation:

The first term in Eq.(24) is just the action for the bosonic string in Eq.(1), the second term is new for the fermionic partner. S0 possesses world sheet reparametrization invariance and global world sheet supersymmetry under the supersymmetry transformation. However, if the transformation is local (i.e., it is a function of  and
and  ), it introduces an extra term, which is cancelled by S1 -
), it introduces an extra term, which is cancelled by S1 -
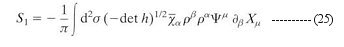
where the two-dimensional supergravity "gravitino" is related to the local supersymmetry transformation by the formula - 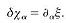 This cancellation scheme in turn gives another extra term, which is finally cancelled by S2 -
This cancellation scheme in turn gives another extra term, which is finally cancelled by S2 -
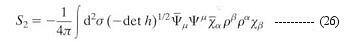
The action S in the form of Eq.(23) is the locally world sheet supersymmetric action for the superstring. In covariant gauge, the equations of motion are:

where J is the supercurrent. Eqs.(29) and (30) amount to the constraint equations, which reduce the degrees of freedom in the theory. The solutions for the bosonic string are similar to those Eqs.(4) and (5). The fermionic degrees of freedom can also be separated into right and left-movers, such as:
is the supercurrent. Eqs.(29) and (30) amount to the constraint equations, which reduce the degrees of freedom in the theory. The solutions for the bosonic string are similar to those Eqs.(4) and (5). The fermionic degrees of freedom can also be separated into right and left-movers, such as:

where 
 is the Dirac spinor with 2D/2 components (in a single-column matrix). It can be decomposed into two Weyl spinors
is the Dirac spinor with 2D/2 components (in a single-column matrix). It can be decomposed into two Weyl spinors  R
R and
and  L
L . If the space-time dimension is taken to be D = 10, then there are 32 components for the Dirac spinor, and 16 each for the Weyl spinors. In the Type IIA and IIB theory, these Weyl spinors have opposite and same chiralities respectively. The Heterotic theories have only one copy of the Weyl spinors. The Type I theory is derived from the Type IIB theory by taking one copy from its even parity sector (and adding open strings and Chan-Paton factors to cancel anomalies).
. If the space-time dimension is taken to be D = 10, then there are 32 components for the Dirac spinor, and 16 each for the Weyl spinors. In the Type IIA and IIB theory, these Weyl spinors have opposite and same chiralities respectively. The Heterotic theories have only one copy of the Weyl spinors. The Type I theory is derived from the Type IIB theory by taking one copy from its even parity sector (and adding open strings and Chan-Paton factors to cancel anomalies).
The surface terms arising from the variation of the action vanish with the boundary conditions:
 |
for closed strings; |
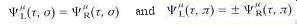 |
for open strings. |
The periodic boundary conditions are referred to as Ramond boundary conditions denoted by R, and the anti-periodic boundary conditions - Neveu-Schwarz boundary conditions, denoted by NS. For the right movers, the mode expansion is:

A similar mode expansion can be written down for the left movers with oscillators 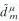 and
and 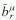 . For the open superstring, the mode expansions of the right and left movers are not independent of each other, i.e.,
. For the open superstring, the mode expansions of the right and left movers are not independent of each other, i.e., 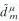 =
= 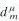 ,
, 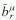 =
= 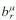 , and the "2n or 2r" in Eqs.(31) and (32) is replaced by "n or r" in the exponent. There is also an additional factor of 1/21/2.
, and the "2n or 2r" in Eqs.(31) and (32) is replaced by "n or r" in the exponent. There is also an additional factor of 1/21/2.
Quantization of the fermionic degrees of freedom is achieved by imposing the canonical anti-commutation relations (with the momenta (i/2 )
)
 R or L):
R or L):

In terms of the mode expansion oscillators, the anti-commutators for Ramond boundary conditions are:

with left- and right-mover oscillators anti-commuting. (Notice that the R or NS boundary conditions may be chosen independently for the right and left movers.)
Additional ghosts from the time-like fermionic oscillator appear in superstring theory. All ghosts can be removed via the light cone gauge in the form of Eq.(22a) and
 + = (
+ = ( 0 +
0 +  D-1)/(2)1/2,
D-1)/(2)1/2,  - = (
- = ( 0 -
0 -  D-1)/(2)1/2 ---------- (37)
D-1)/(2)1/2 ---------- (37)
It can be shown that a local world sheet supersymmetry transformation may be used to choose  + = 0; while
+ = 0; while  - can be expressed in terms of the transverse degrees of freedom with
- can be expressed in terms of the transverse degrees of freedom with  = 1, ..., D-2. Once again, there is no more time component and thus no more ghost states. However, in this case the removal of anomaly demands the dimension of the coordinate system to be ten, i.e., D = 10 (instead of D = 26 for the bosonic string). Tachyon also occurs in the super-string theory. The GSO projection is used to impose extra restriction for the removal of some unwanted states including the tachyon. Following the same procedure as in the case of bosonic string, the mass sqaure for the superstring is:
= 1, ..., D-2. Once again, there is no more time component and thus no more ghost states. However, in this case the removal of anomaly demands the dimension of the coordinate system to be ten, i.e., D = 10 (instead of D = 26 for the bosonic string). Tachyon also occurs in the super-string theory. The GSO projection is used to impose extra restriction for the removal of some unwanted states including the tachyon. Following the same procedure as in the case of bosonic string, the mass sqaure for the superstring is:

In the NS sector the correcponding result is:

Thus, the world of elementary particles are unified by a tiny string, which would represent all the particles according to its vibrational frequency.
.

 (
( ,
, ) to a fermionic partners
) to a fermionic partners 
 (
( ,
, ), which are two-component world sheet spinors. The action S consists of three parts:
), which are two-component world sheet spinors. The action S consists of three parts:
 and
and  ), it introduces an extra term, which is cancelled by S1 -
), it introduces an extra term, which is cancelled by S1 -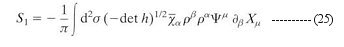
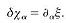 This cancellation scheme in turn gives another extra term, which is finally cancelled by S2 -
This cancellation scheme in turn gives another extra term, which is finally cancelled by S2 -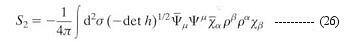

 is the supercurrent. Eqs.(29) and (30) amount to the constraint equations, which reduce the degrees of freedom in the theory. The solutions for the bosonic string are similar to those Eqs.(4) and (5). The fermionic degrees of freedom can also be separated into right and left-movers, such as:
is the supercurrent. Eqs.(29) and (30) amount to the constraint equations, which reduce the degrees of freedom in the theory. The solutions for the bosonic string are similar to those Eqs.(4) and (5). The fermionic degrees of freedom can also be separated into right and left-movers, such as:

 is the Dirac spinor with 2D/2 components (in a single-column matrix). It can be decomposed into two Weyl spinors
is the Dirac spinor with 2D/2 components (in a single-column matrix). It can be decomposed into two Weyl spinors  R
R and
and  L
L . If the space-time dimension is taken to be D = 10, then there are 32 components for the Dirac spinor, and 16 each for the Weyl spinors. In the Type IIA and IIB theory, these Weyl spinors have opposite and same chiralities respectively. The Heterotic theories have only one copy of the Weyl spinors. The Type I theory is derived from the Type IIB theory by taking one copy from its even parity sector (and adding open strings and Chan-Paton factors to cancel anomalies).
. If the space-time dimension is taken to be D = 10, then there are 32 components for the Dirac spinor, and 16 each for the Weyl spinors. In the Type IIA and IIB theory, these Weyl spinors have opposite and same chiralities respectively. The Heterotic theories have only one copy of the Weyl spinors. The Type I theory is derived from the Type IIB theory by taking one copy from its even parity sector (and adding open strings and Chan-Paton factors to cancel anomalies). 
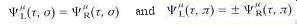

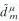 and
and 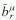 . For the open superstring, the mode expansions of the right and left movers are not independent of each other, i.e.,
. For the open superstring, the mode expansions of the right and left movers are not independent of each other, i.e., 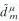 =
= 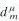 ,
, 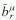 =
= 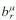 , and the "2n or 2r" in Eqs.(31) and (32) is replaced by "n or r" in the exponent. There is also an additional factor of 1/21/2.
, and the "2n or 2r" in Eqs.(31) and (32) is replaced by "n or r" in the exponent. There is also an additional factor of 1/21/2. )
)
 R or L):
R or L):

 + = (
+ = ( 0 +
0 +  D-1)/(2)1/2,
D-1)/(2)1/2,  - = (
- = ( 0 -
0 -  D-1)/(2)1/2 ---------- (37)
D-1)/(2)1/2 ---------- (37) + = 0; while
+ = 0; while  - can be expressed in terms of the transverse degrees of freedom with
- can be expressed in terms of the transverse degrees of freedom with  = 1, ..., D-2. Once again, there is no more time component and thus no more ghost states. However, in this case the removal of anomaly demands the dimension of the coordinate system to be ten, i.e., D = 10 (instead of D = 26 for the bosonic string). Tachyon also occurs in the super-string theory. The GSO projection is used to impose extra restriction for the removal of some unwanted states including the tachyon. Following the same procedure as in the case of bosonic string, the mass sqaure for the superstring is:
= 1, ..., D-2. Once again, there is no more time component and thus no more ghost states. However, in this case the removal of anomaly demands the dimension of the coordinate system to be ten, i.e., D = 10 (instead of D = 26 for the bosonic string). Tachyon also occurs in the super-string theory. The GSO projection is used to impose extra restriction for the removal of some unwanted states including the tachyon. Following the same procedure as in the case of bosonic string, the mass sqaure for the superstring is:
