Home Page Overview Site Map Index Appendix Illustration About Contact Update FAQ


Holographic Principle

Contents

Holographic Principle
Holography
Black Hole Entropy
Holographic Universe
Holographic Space-time

Holographic Principle

Holographic Principle is about encoding information from (D+1)-dimensional space onto D-dimensional space. It can be the interference pattern on a photographic plate from a three-dimensional object, or the entropy impressed on the surface of a black hole, or a physical theory translated into another form. Such principle is now embraced by some physicists, who claim that it will become part of the foundations of new physics, from which quantum theory and relativity may both deduced as special cases. The followings will explored the above-mentioned examples in more detail.

[Top]

Holography

Holography was invented in 1947 with the advancement of laser technology. It is a photographic process which does not capture an image of the object being photographed, as is the case with the conventional technique, but rather records the phases and amplitudes of
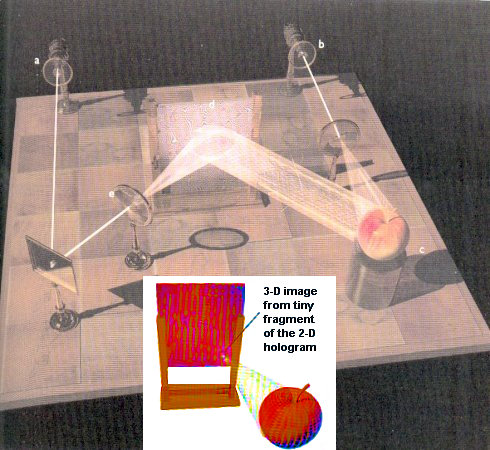
inflation light waves reflected from the object. The wave amplitudes are readily encoded on an ordinary photographic film. The phases are recorded as interference patterns produced by the reflected light and a reference coherent light (from the same laser). Each point on the hologram received light reflected from every part of the illuminated object and, therefore, contains the complete visual record of the object as a whole. When the hologram obtained from the development of a film exposed in this way is placed in a beam of coherent light, two sets of strong diffracted waves are produced - each an exact replica of the original signal bearing waves that impinged on the plate when the hologram was made. One set of diffracted waves produces a virtual image, which can be seen by looking through the hologram. It appears in a complete three-dimensional form with highly realistic perspective effects. In fact, the reconstructed picture has all the visual properties of the original object.

Figure 01 Holography
[view large image]

 Figure 01depicts the process of making a hologram:


The small insert in Figure 01 shows the reproduced three-dimensional virtual image in the reversed process.

[Top]

Black Hole Entropy

    Theoretical physicists has suggested that entropy or information of matter-energy inside the black hole is encoded on the surface of the event horizon similar to holography, which stores information in 3-dimensional space on a 2-D flat sheet. The derivation is surprisingly simply as shown in the following.

  1. The derivation begins by throwing a photon with wavelength into the black hole with mass m and radius R. In order to approach the black hole in an un-defined location, the wavelength should be about the size of the event horizon, namely, ~ R.
  2. The energy carries by such photon is E = h = hc/ = 2c/R.
  3. The corresponding increase in mass would be m = E/c2 = 2/Rc (via the most celebrated formula E = mc2).
  4. The increase in surface area at the event horizon can be calculated from the definition R = 2Gm/c2, and yield:
    RR = 4 (G/c3) = 4 (LPl)2,
    where G/c3 = (LPl)2 = (1.62x10-33 cm)2 is the Planck area - the smallest area (the most basic unit) conceivable before the full impact of quantum gravity set in.
  5. Thus the number of basic unit on the event horizon surface area ASh is:
    n = ASh/RR = ASh/[4(LPl)2].
  6. Since the basic unit is either present or absent at any point on the surface, the number of arrangements is N = 2n.
  7. According to definition, the absolute value of information | I | = log2(N) = n = (RSh)2/(LPl)2 = 1.2x1066 (RSh)2 bits, where we have used the formula ASh = 4(RSh)2. Note that the entropy S = (kBln2) | I |, where kB is the Boltzmann constant.
inflation If originally a roughly spherical distribution of matter is contained inside an area A', the matter is induced to collapse to form a black hole as shown in diagram (a), Figure 02. Then the black hole's area A must be smaller than A', so its entropy must be less than (c3/G)(A'/4). Because entropy cannot decreases, so the original entropy must be less than that as well. This is the holographic bound as shown in diagram (c), Figure 02.

The "universal entropy bound" is an even more stringent limit on the amount of entropy or information that can be contained within a volume of space. This time we throw some macroscopic mass m with radius R = d/2 into the black hole. It is derived by imaging that a capsule of matter is engulfed by a black hole about the same size (see diagram (b), Figure 02). The small increase in the black hole's size places a limit on how much entropy the capsule could have contained. If we put water in the capsule, then m = water(4/3)R3. Thus the increment in event horizon surface area is A = 8RR = 8(2G/c2)water(4/3)R4.

Figure 02 Black Hole En-tropy [view large image]

 Following the prescription in the previous derivation, the increment in information is:
|I| = (c3/G)(A/4) 2x1039 R4 bits.

This is plotted as the red line in diagram (c), Figure 02. The holographic and universal information bounds are far beyond the data storage capacities of any current technology, and they greatly exceed the density of information on chromosomes and the thermodynamic entropy of water (see diagram (c), Figure 02). This example demonstrates that the entropy or information in a 3-dimensional volume can be related to the 2-dimensional surface area of a black hole. The maximum allowable information on this surface area can be interpreted as the maximum allowable number of smallest units on such surface. This smallest unit has the size of Planck area as envisioned in the "Loop Quantum Theory". According to this theory, the Planck area is a single quantum of space-time - it cannot get any smaller than that.

[Top]

Holographic Universe

The GEO600 gravitational wave detector with two 600 meters arms (Figure 03a) has not detected any signal so far. However for many months lately in 2008, inexplicable noise is plaguing the giant detector. One novel explanation suggests that this is the noise of space-time jitter projected from the surface of the event horizon to appear as hologram in our 3-D space. The encoding of information on the 2-D event horizon surface is similar to that in a black hole as mentioned above. What's special in this case is the realization that the number of information on the surface must match the number of bits contained inside the volume of the universe. Since the storage is bigger in the volume than on the surface, the world inside must be made up of grains bigger than the smallest space-time unit in Planck length of
GEO600 1.6x10-33 cm (on the surface of the event horizon). It turns out to be around 3x10-13 cm as calculated from the size of the universe at about 1028 cm and the number of information n at the surface of the event horizon derived above (in the section for "Black Hole Entropy"). Or, to put it another way, a holographic universe is blurry, but the grainy structure is much easier to detect. Quantum effects will cause the space-time quanta to convulse wildly resulting in the noise picked up by GEO600. If this interpretation is proven to be correct, it will be ranked at the same level of achievement as the discovery of the CMBR, which also appeared as noise in the microwave detector.

Figure 03a GEO600 Detector [view large image]
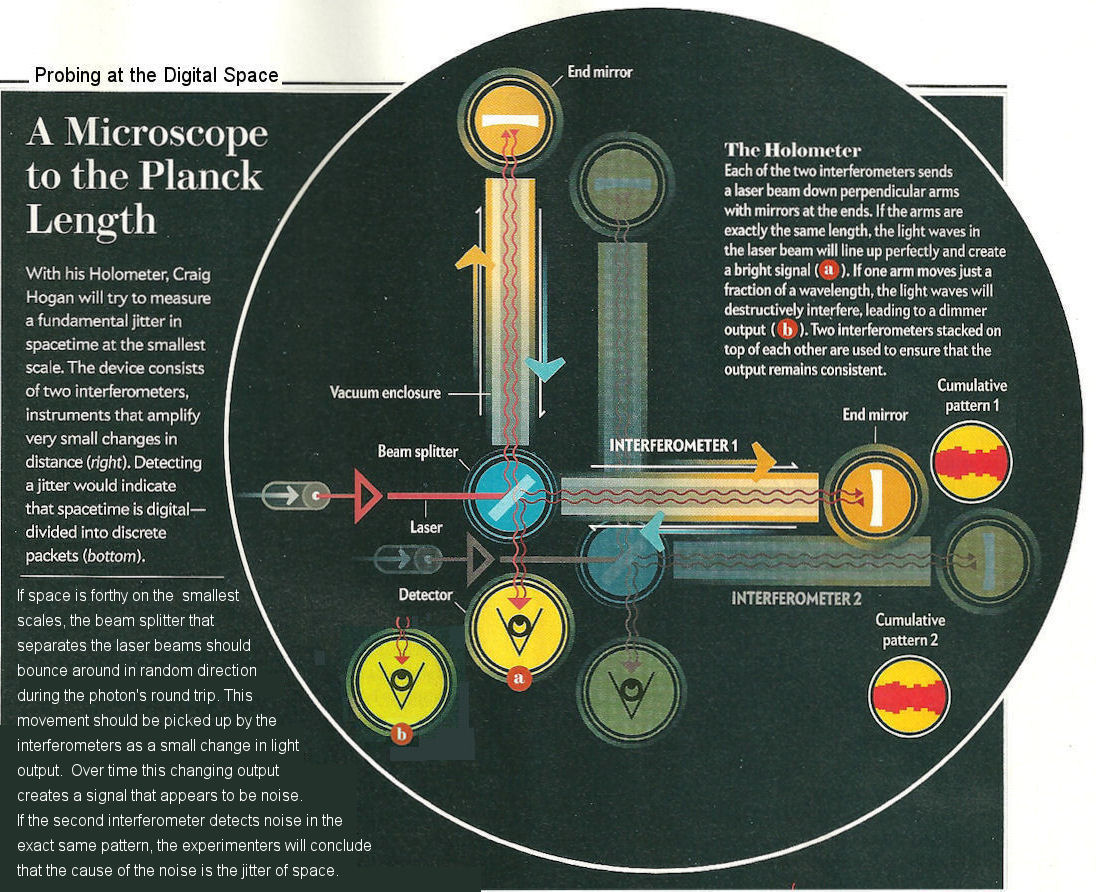Probing the Quantum Space According to an article in the February 2012 issue of Scientific American, an experiment is being built in an abandoned shed at the now defunct Fermilab to probe the jitter of quantum space, which may be much larger than the Planck size as explained above. The setup is similar to the GE0600 experiment but with shorter arms at 40 meters (Figure 03b). In fact both of them are similar to the Michelson-Morley experiment in 1887 except that they are looking for something else this time round. Instead of going after the speed of light in the two arms, measurement of the jitter of space depends on the tiny movement of the beam splitter as the supporting space thrashing whichever way due to quantum fluctuation. It is similar to a boat pitching on the sea. The result could be a pattern of noise as shown in Figure 03b. A second interferometer is under the first one to make sure the measurement is repeatable.

Figure 03b [view large image] Probing at Quantum Space

[Top]

Holographic Space-time

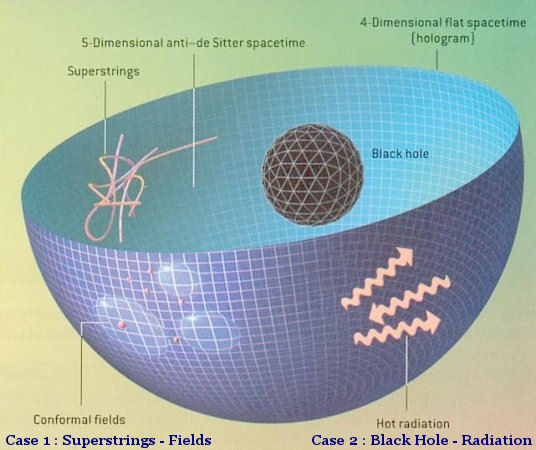inflation Another example of the holographic principle at work involves the Euclidean Anti-de Sitter (AdS) space, which expands and possesses a boundary at infinity - much like our universe. The metric of such space has the form:

ds2 = dr2 + sinh2(r) d42

where d42 is the (3+1)-D hypersphere at the boundary of the (4+1)-D Euclidean AdS space, where the (n+1)-D denotes n spatial and 1 temporal dimensions.

Figure 04 Holographic Space-time [view large image]
Using such (4+1)-D space, theorists have devised an example in which an AdS universe described by strongly coupled string theory corresponds to weakly coupled point particle conformal§ field theory on the (3+1)-D boundary of that space (Figure 04), and vice versa. Examples of this holographic correspondence are now known for space-times with a variety of dimensions. The holographic equivalence can allow a difficult calculation in the (3+1)-D boundary space-time, such as the behaviour of quarks and gluons, to be traded for another, easier calculation in the highly symmetric, (4+1)-D space-time or vice versa. It has also been shown that a black hole in (4+1)-D space-time corresponds to hot radiation (e.g., the quark-gluon plasma) in the (3+1)-D hologram. This is the argument for conservation of information in the debate of whether it is lost once falling into a black hole. See "Entanglement and Holographic Space-time" for detail.

4-D Supernova A cosmological model based on the collapse of a four dimensional star was unveiled in 2014 (Figure 05). It shows that the three dimensional Holographic projection of this event corresponds to the Big Bang in our universe. The expanding shell of the 4-D supernova maps to our 3-D expansion. Its novel property includes an event horizon, which shields the singularity bothering so many cosmologists. The smoothness and flatness of our universe is just a reflection of the 4-D bulk, which had been in existence for a much longer time. The study suggests that the CMBR may reveal the spin and the presence of 4-D matter around the 4-D black hole.

Figure 05 4-D Supernova
[view large image]

§ A conformal field theory (CFT) is a quantum field theory that is invariant under the conformal transformations such that under the coordinate transformations x x', the metric is unchanged up to a rescaling: . These are precisely the coordinate transformations that preserve the angle between two vectors, hence the name "conformal transformations". The conservation of the angular size in such transformation is readily apparent from the definition of angle in Riemannian geometry:

cos(A) = gijuivj/(|gijuiuj||gijvivj|)1/2 = g'ijuivj/(|g'ijuiuj||g'ijvivj|)1/2

where gij is the metric tensor, ui and vj are the ith and jth components of the two unit vectors respectively. For Examples:
On a flat surface the metric ds2 = dx2 + dy2, g11 = g22 = 1, and g12 = g21 = 0, while on a spherical surface ds2 = r2d2 + r2sin2d2 (with r = constant), g11 = r2, g22 = r2sin2, and g12 = g21 = 0.

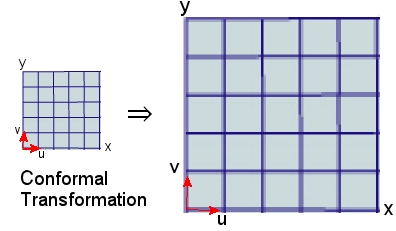Conformal Transformation Conformal Mappings For the case of 2 unit vectors at the x and y axis respectively on a flat surface, u = (1,0), v = (0,1); cos(A) = 0 or A = 90o. Now consider ds2 = g11dx2 + g22dy2, if we make a conformal transformation x = ax', y = ay', where "a" is a constant. It follows that the new metric tensors become g'11 = g'22 = a2. This kind of transformation will distort the distance between points, but the angle "A" remains unchanged (Figure 06). This is similar to the comoving frame in cosmic expansion. Figure 07 shows some more fanciful conformal mappings.

Figure 06 Conformal Transformation [view large image]

Figure 07 Conformal Mappings