
---------- (40)
---------- (41)
---------- (42)
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 E term in Eq.(40), and thus put the equations into a consistent set which implied new physical phenomena, at that time unknown but subsequently verified in all details by experiments. In terms of the electric field E and magnetic field B the Maxwell's equations are four first order differential equations :
E term in Eq.(40), and thus put the equations into a consistent set which implied new physical phenomena, at that time unknown but subsequently verified in all details by experiments. In terms of the electric field E and magnetic field B the Maxwell's equations are four first order differential equations : |
---------- (39) ---------- (40) ---------- (41) ---------- (42) |
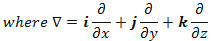 ,
, is the charge density with charge Q, and c is the velocity of light. The conversion of the laws from differential to integral form is accomplished by applying the Gauss's and the Stoke's theorems as shown below via a much simplified derivation with either a cube or square (the circle on the integral sign denotes either a closed surface or loop).
is the charge density with charge Q, and c is the velocity of light. The conversion of the laws from differential to integral form is accomplished by applying the Gauss's and the Stoke's theorems as shown below via a much simplified derivation with either a cube or square (the circle on the integral sign denotes either a closed surface or loop).

 (
(
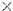 A)=0, Eq.(41) can be defined by the vector potential A:
A)=0, Eq.(41) can be defined by the vector potential A:
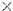 A ---------- (43)
A ---------- (43)
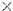 (
(
 )=0, we can define E in terms of A and the scalar potential
)=0, we can define E in terms of A and the scalar potential  as :
as :
 - (1/c)
- (1/c) A ---------- (44)
A ---------- (44) 2
2 + (1/c)
+ (1/c) (
(
 A) = 0 ---------- (45)
A) = 0 ---------- (45)
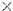 (
(
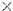 ) A = -
) A = - 2A +
2A +  (
(
 A), we get another second order differential equation :
A), we get another second order differential equation : 2A - (1/c2)
2A - (1/c2) A -
A -  (
(
 A + (1/c)
A + (1/c)
 ) = 0 ---------- (46)
) = 0 ---------- (46)
 A + (1/c)
A + (1/c)
 = 0,
= 0, 2A - (1/c2)
2A - (1/c2) A = 0 ---------- (46a),
A = 0 ---------- (46a), 2
2 - (1/c2)
- (1/c2)
 = 0 ---------- (45a).
= 0 ---------- (45a).
 form a four potential, whcih are prescribed by the Lorentz invariant wave equations of Eqs. (46a), (45a). The formulation is now suitable for use in high energy particle physics. The Lorenz condition is also manifest Lorentz invariance (note the two names differ by a "t"), but is incomplete in the sense that the definition of B in Eq.(43) is unchanged by adding a term in the form of the "gradient of scalar function
form a four potential, whcih are prescribed by the Lorentz invariant wave equations of Eqs. (46a), (45a). The formulation is now suitable for use in high energy particle physics. The Lorenz condition is also manifest Lorentz invariance (note the two names differ by a "t"), but is incomplete in the sense that the definition of B in Eq.(43) is unchanged by adding a term in the form of the "gradient of scalar function  " because of the identity
" because of the identity 
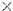 (
(
 ) = 0. It follows that E, B and Eqs.(45a), (46a) are unchanged by the transformation :
) = 0. It follows that E, B and Eqs.(45a), (46a) are unchanged by the transformation : A' = A +
A' = A + 
 ---------- (47)
---------- (47)

 ' =
' =  - (1/c)
- (1/c)
 ---------- (48)
---------- (48) 2
2 - (1/c2)
- (1/c2)
 = 0.
= 0. involves setting
involves setting  2
2 = -
= -
 A, and eliminating the longitudinal component with
A, and eliminating the longitudinal component with  = (1/c)
= (1/c)
 in the transformation Eqs.(47), and (48). In this way, the transversality condition
in the transformation Eqs.(47), and (48). In this way, the transversality condition 
 A' = 0 is ensured. This condition is also known as "Coulomb gauge". It follows that :
A' = 0 is ensured. This condition is also known as "Coulomb gauge". It follows that : 
 A' = 0.
A' = 0. ' = 0 in free space without the presence of any source, the wave equation Eq.(46) become :
' = 0 in free space without the presence of any source, the wave equation Eq.(46) become : 2A' - (1/c2)
2A' - (1/c2) A' = 0 ---------- (49)
A' = 0 ---------- (49)
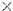 A' ---------- (50)
A' ---------- (50) A' ---------- (51)
A' ---------- (51) 2E - (1/c2)
2E - (1/c2) E = 0 ---------- (50a)
E = 0 ---------- (50a) 2B - (1/c2)
2B - (1/c2) B = 0 ---------- (51a)
B = 0 ---------- (51a)
 /L (n =
/L (n =  1,
1,  2, ...) with k
2, ...) with k x = k
x = k x -
x -  t = k
t = k x - |k|ct. The ck coefficients is linked to the spectrum associated with the electromagnetic radiation. It will assume the role of q-number in second quantization, which endows particle attributes to the wave.
x - |k|ct. The ck coefficients is linked to the spectrum associated with the electromagnetic radiation. It will assume the role of q-number in second quantization, which endows particle attributes to the wave.