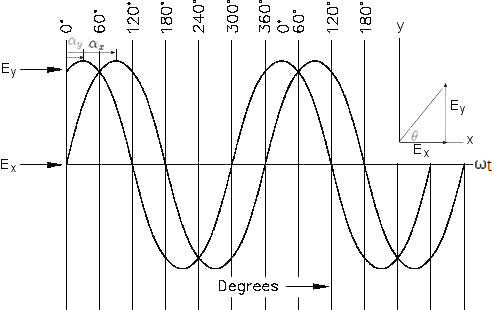
Ex = Ex0 cos(
 t - kz +
t - kz +  x) ---------- (53a)
x) ---------- (53a)Ey = Ey0 cos(
 t - kz +
t - kz +  y) ---------- (53b)
y) ---------- (53b)where Ex0, Ey0 are amplitudes, and
 x,
x,  y are the phase angles of the x, y components respectively (Figure 07b). These equations can be simplified somewhat if the view is facing the x-y plane fixed at z=0 (such as the view in Figure 07c), and by using the relative phase angle
y are the phase angles of the x, y components respectively (Figure 07b). These equations can be simplified somewhat if the view is facing the x-y plane fixed at z=0 (such as the view in Figure 07c), and by using the relative phase angle  =
=  x -
x -  y :
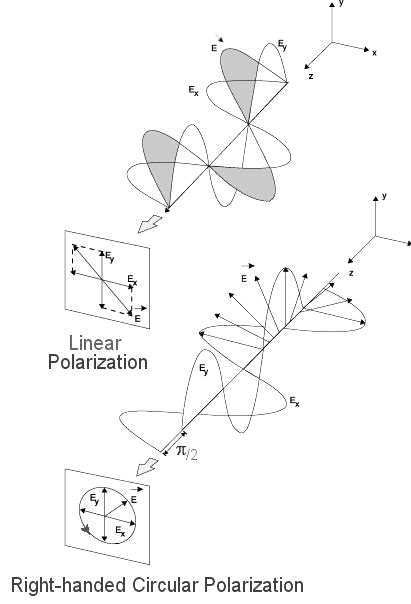
y : Figure 07a Polari-zation 
Figure 07b Phase Angles
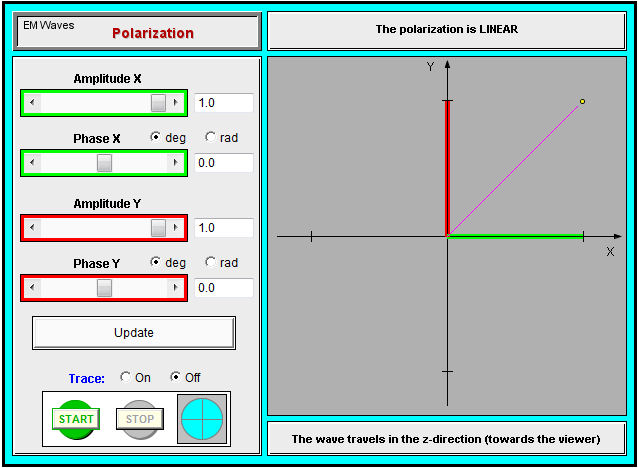
[view large image]
 t) ---------- (53c)
t) ---------- (53c)Ey = Ey0 cos(
 t -
t -  ) ---------- (53d)
) ---------- (53d) = tan-1(Ey/Ex) = tan-1{(Ey0/Ex0)[cos(
= tan-1(Ey/Ex) = tan-1{(Ey0/Ex0)[cos(
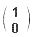 and |ey> =
and |ey> = 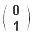 are the unit vector in the x (upper component) and y (lower component) directions respectively. It is similar to the Jones vector in classical electrodynamics and the polarization vectors in Eq.(52). Since the unit vectors satisfies the orthogonality relation : < ei|ej> =
are the unit vector in the x (upper component) and y (lower component) directions respectively. It is similar to the Jones vector in classical electrodynamics and the polarization vectors in Eq.(52). Since the unit vectors satisfies the orthogonality relation : < ei|ej> =  (i-j) for (i, j) = (x or y), < e|e> = 1. If it is interpreted as the total probability, then cos2
(i-j) for (i, j) = (x or y), < e|e> = 1. If it is interpreted as the total probability, then cos2 ) |eL> + (ei
) |eL> + (ei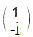 /
/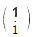 /
/ [E(r,t)
[E(r,t)  c) ---------- (53m)
c) ---------- (53m) U/|
U/|
