Calabi-Yau Manifold

The Connections

	The connection between string theory and Calabi-Yau manifold is mainly through supersymetry (Figure 22), although there are other linkages that make it even more desirable. Followings are a brief description of the steps leading to this unique selection, and its other special properties beneficial to the development of the Superstring theory.
Figure 22 Connection 1 to Calabi-Yau Manifold [view large image]

String - The initial theory of the bosonic string corresponds in low energy limit to particles with integer spin, i.e., they are all bosons. This theory is plagued with a lot of problems, parts of which can be eliminated by going to a space of 26 dimensions. The remaining problems of tachyon and missing fermions can be resolved only by adding supersymmetry into the theory.
Supersymmetry - Supersymmetry is used to add fermions into the bosonic string theory. It requires a ten dimensional space time to eliminate the anomlies, inconsistencies, techyons, etc. Thus, the 26 dimensional space for the bosons has to be compacted preliminarily to ten extra dimensions by rolling up 16 to tiny circles or set to zero. If the N = 1 version of the super generator is selected, then it seems to incorporate the chiral character of the fermions nicely as well (see Table 02).
Compactification - The remaining six extra dimensions have to be reduced further to small size. The task became more difficult as the chiral characteristic does not survive the compactification process rendering the theory inconsistent with the real world. It does not work for a simple circle or torus or other more complicate manifolds such as the K3 surface (a 4 real or 2 complex dimensional manifold).
Parity Violation - Parity violation in weak interaction is an established fact since 1956. Only the left-handed leptons participated in the interaction. Thus the left- and right-handed leptons are different (chiral), all the realistic theories have to accommondate to this fact. Subsequent investigations show that only the compact (finite) Kahler manifold of SU(3) (6 real or 3 complex dimensions) holonomy with vanishing first Chern class and zero Ricci curvature can preserve the chiral characteristic after compactification.
Calabi-Yau Manifold - As mentioned in the section of "Calabi-Yau Manifold for Dummies", all the above-mentioned

requirements are satisfied by the Calabi-Yau manifold as if it is "made to order" for the occasion. By the way, it also correctly reproduce the three generations for the fermions, and is itself a solution of the 6-D field equation in General Relativity (producing the gravitino). However, it took nine years between the proof of the "Calabi-Yau Conjecture" in 1976 and the introduction of this strange geometry object to the Superstring theory in 1985 for the mathematics and physics to connect. Since then there are also Calabi-Yau off-Broadway show, Calabi-Yau painting (Figure 23), and Calabi-Yau joke in a New Yorker satire by Woody Allen - all wanted to cash in on its fame.

Figure 23 Calabi-Yau Monna Lisa [view large image]

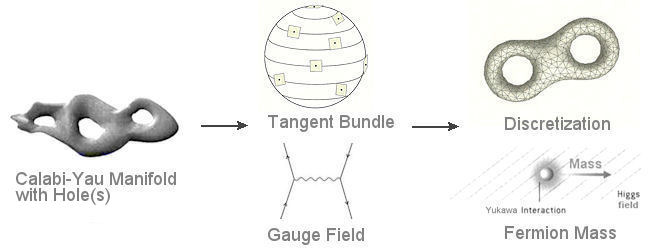Further efforts to reproduce the Standard Model in 1986 and later reveal another connection between the Superstring theory and Calabi-Yau manifold. A new theory such as the Superstring theory should recover all the features of an effective theory at lower level. This test would be a show stopper if it fails. The investigations showed that it is possible to obtain all the 12 gauge fields with the Calabi-Yau manifold. Work is also in progress to calculate the ferimon mass from the manifold - a feat not included in

Figure 24 Connection 2 to Calabi-Yau Manifold [view large image]

the Standard model. Figure 24 shows the new connection, which is also explained in more detail below :

Calabi-Yau Manifold (with holes) - It has been shown that there are specific requirements in the Superstring theory leading to the selection of the Calabi-Yau manifold for compactification. It was then discovered that only the manifold with three holds could produce the three generations of fermions as observed in the real world. The presence of holes in the manifold inevitably affects the geometry and topology, which in turn affects physics in such a lucky way as to enable the recovery of the Standard model from the Superstring theory.
Gauge Fields - It is found that the SU(3)xSU(2)xU(1) gauge groups is not directly linked to the Calabi-Yau manifold. It is instead connected through the "tangent bundle" of the Calabi-Yau manifold. The "tangent bundle" is an additional manifold created by collecting all the tangent planes on the manifold as shown in a 2-D example in Figure 24. The term "bundles" is used by mathematicians to express the "gauge fields" in physics. It has been shown that the tangent bundles (actually any bundles for the Cababi-Yau manifold) is equivalent to the Yang-Mills equations (with N = 1 supersymmetry) and thus makes the connection to the massless version of the Standard model. Later on it was also shown that any bundles (of the Calabi-Yau manifold) can satisfy the anomaly cancellation requirement if its second Chern class equals the second Cheren class of the tangent bundle.
Fermion Mass - Beyond getting the right particles, the Superstring theory has the potential to yield the mass of fermions and places itself above the Standard model. The mass of ferimon is proportional to the Yukawa coupling constant g, which is in turn determined by the triple product in the six dimensional Calabi-Yau space, where and are the fermion and Higgs fields respectively. Since the value of the fields depends on the location in the Calabi-Yau manifold, it is necessary to perform numerical integration over the six dimensional Calabi-Yau space to obtain the average by a process called "discretization" - a process that defies today's computer power. Another way to compute g is through "embedding" the Calabi-Yau manifold in a higher dimensional background space. But so far no one has been able to work out the coupling constant g or mass for any fermion. Anyway, this is one example of the attempts to derive fundamental constants in the 3+1 large dimensions from the 6 dimensional compactified space.