By quantizing the dimensionless scale factor R and its time derivative dR/dt, this particle is endowed with a wave property; the corresponding wave function
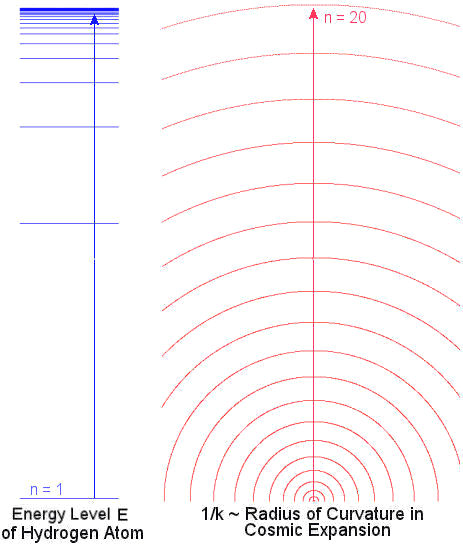
 can be interpreted as the probability amplitude at certain value of the scale factor R. It turns out that the resulting wave equation is similar to that for the electron in the hydrogen atom (with different interpretations of the parameters). In particular, the energy in the case of hydrogen atom is now replaced by the spatial curvature k. The transition from its extremely large value to small number corresponding to a nearly flat space can be interpreted as quantum jump to near continuum during the period of inflation. Figure 01a compares the energy levels of the hydrogen atom and the inverse of the spatial curvature (~ radius of curvature) in cosmic expansion. The appearance seems to be in reverse since the correspondence is between E (energy level) and k (spatial curvature), and the plot is for 1/k to make it looking like the expansion of the universe. This formulation is similar to the Wheeler-DeWitt equation, which is also derived from the Friedmann equation with an un-specified potential.
can be interpreted as the probability amplitude at certain value of the scale factor R. It turns out that the resulting wave equation is similar to that for the electron in the hydrogen atom (with different interpretations of the parameters). In particular, the energy in the case of hydrogen atom is now replaced by the spatial curvature k. The transition from its extremely large value to small number corresponding to a nearly flat space can be interpreted as quantum jump to near continuum during the period of inflation. Figure 01a compares the energy levels of the hydrogen atom and the inverse of the spatial curvature (~ radius of curvature) in cosmic expansion. The appearance seems to be in reverse since the correspondence is between E (energy level) and k (spatial curvature), and the plot is for 1/k to make it looking like the expansion of the universe. This formulation is similar to the Wheeler-DeWitt equation, which is also derived from the Friedmann equation with an un-specified potential. Figure 01a Energy Level and Cosmic Expansion 
 -only" is explored in the section on "Quantization of the Empty Universe".
-only" is explored in the section on "Quantization of the Empty Universe". , where px = m dx/dt is the momentum along the x axis. This equation is satisfied if px = -i
, where px = m dx/dt is the momentum along the x axis. This equation is satisfied if px = -i . In order to follow this quantization rule for the case of cosmic expansion, we can assign R to take the place of x and construct an entity having the dimension of ergs-sec = gm-cm2/sec (the dimension of
. In order to follow this quantization rule for the case of cosmic expansion, we can assign R to take the place of x and construct an entity having the dimension of ergs-sec = gm-cm2/sec (the dimension of  , this equation can be re-cast to :
, this equation can be re-cast to : (-1)j[n!/(n-j-1)!(j+1)!j!]xj
(-1)j[n!/(n-j-1)!(j+1)!j!]xj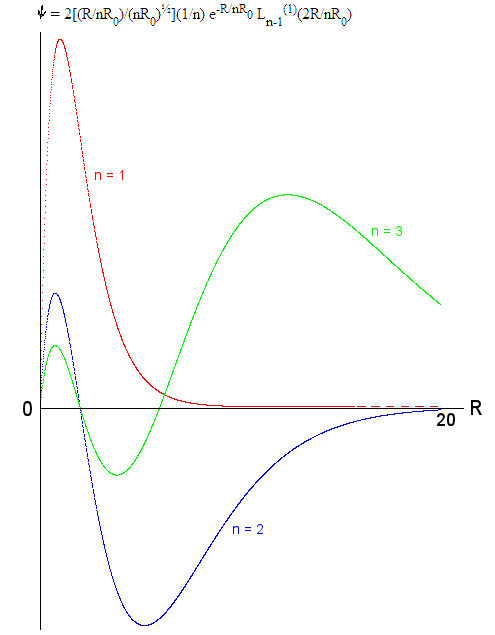


 = nLp would be the radius of curvature as depicted in
= nLp would be the radius of curvature as depicted in  2x1034, the spatial curvature would lower drastically to k
2x1034, the spatial curvature would lower drastically to k  Ra| would not be larger than Ra, thus |
Ra| would not be larger than Ra, thus | Ra
Ra  T/T
T/T 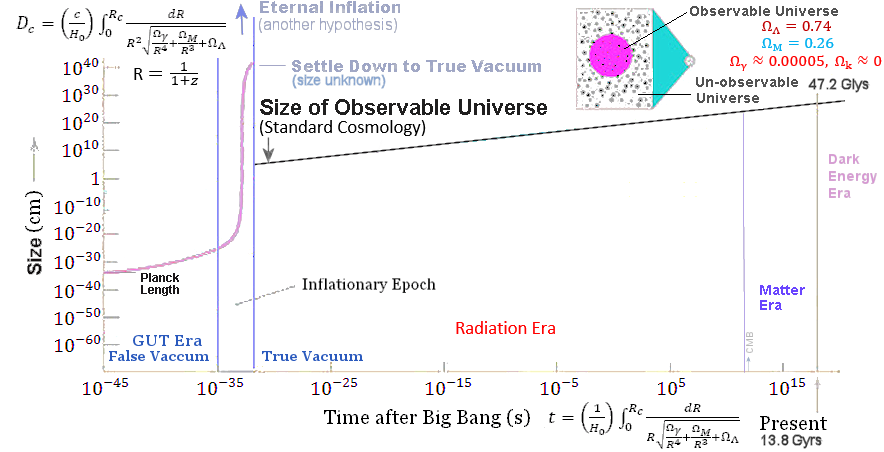

 G)
G) 


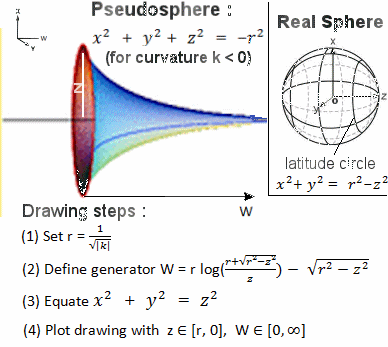
 ---------- (13a),
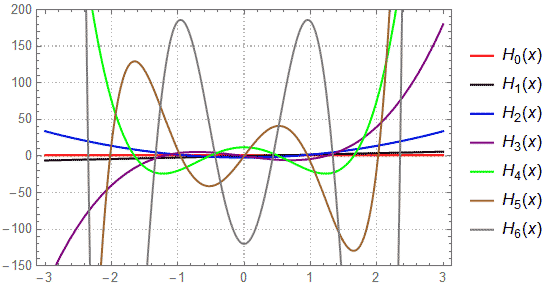
---------- (13a), /m, and Hn(y) is the Hermit Polynomials (see Figures 01h, 01i).
/m, and Hn(y) is the Hermit Polynomials (see Figures 01h, 01i).



 (R0/2) eHt for t
(R0/2) eHt for t  , i.e., the universe expands forever leading to "
, i.e., the universe expands forever leading to "

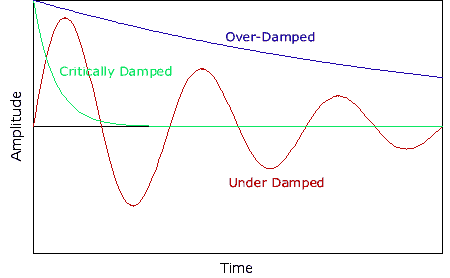
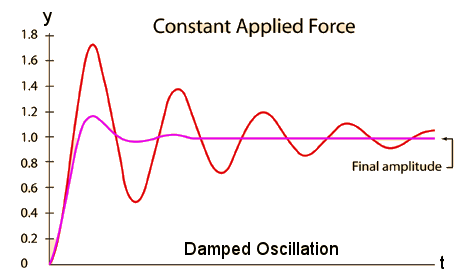


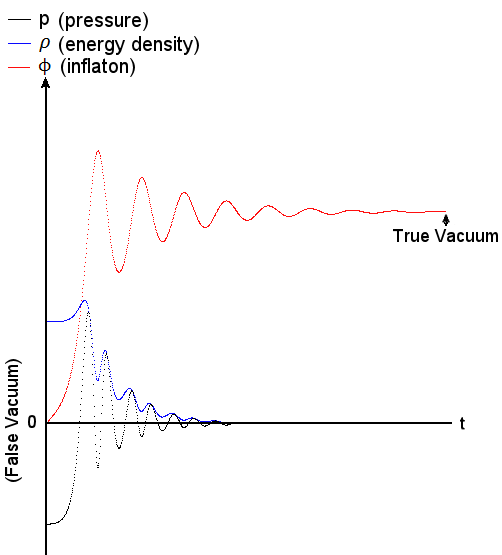


 /4!)
/4!)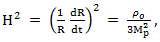





 2)/dk = A, the variance receives equal contributions from a given range of k. The gravitational potential fluctuation is said to be scale invariance as shown in Figure 05d. It is estimated that
2)/dk = A, the variance receives equal contributions from a given range of k. The gravitational potential fluctuation is said to be scale invariance as shown in Figure 05d. It is estimated that 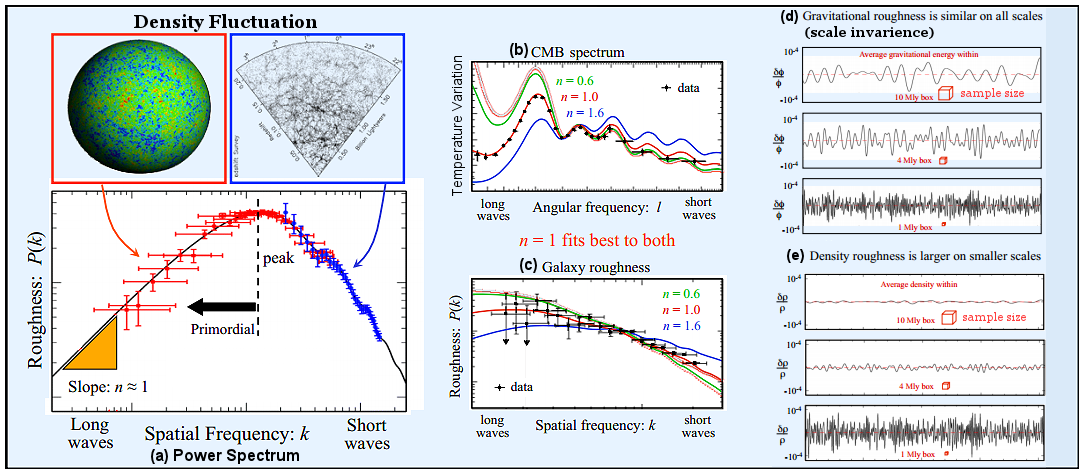








 k for the mass density spectrum (Figure 05i). Subsequent interaction with the
k for the mass density spectrum (Figure 05i). Subsequent interaction with the  ~ 1021cm - about 10-2 times the observable cosmic size of 1023cm at recombination (see "
~ 1021cm - about 10-2 times the observable cosmic size of 1023cm at recombination (see " generated in the early universe. It turns out that both of them obey the same equation for the
generated in the early universe. It turns out that both of them obey the same equation for the 

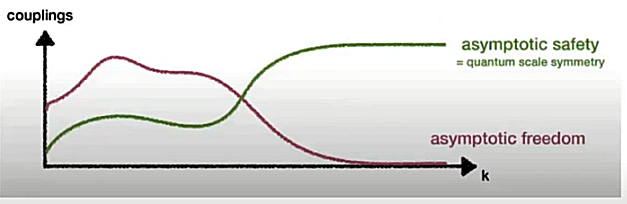
 see this illustration on separation of various theories. AND :
see this illustration on separation of various theories. AND :