 |
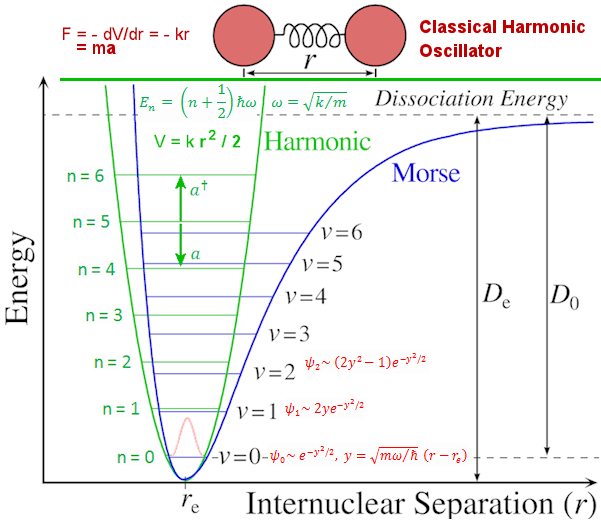
Instead of using the force to describe the dynameics of the system as in Newtonian mechanics, quantum mechanics is usually prescribed by energy (i.e., in the form of the Hamiltonian
H = p2/2m + m 2x2/2, where p = -i 2x2/2, where p = -i  d/dx, and d/dx, and  2 = k/m) in the Schrodinger equation 2 = k/m) in the Schrodinger equation
H n = En n = En n. The eigen value (energy level) is En = (n + 1/2) n. The eigen value (energy level) is En = (n + 1/2)   . The zero point energy . The zero point energy   /2 usually is subtracted from the formula to avoid infinite energy in the vacuum. The wave functions can be expressed in terms of the Hermite Polynomials Hn(x), i.e., /2 usually is subtracted from the formula to avoid infinite energy in the vacuum. The wave functions can be expressed in terms of the Hermite Polynomials Hn(x), i.e.,  n(x) = Cn e-x2Hn. The explicit forms for few low lying states are shown in Figure 06. The formulation of quantum harmonic motion is useful in studying the vibrational modes of molecules and n(x) = Cn e-x2Hn. The explicit forms for few low lying states are shown in Figure 06. The formulation of quantum harmonic motion is useful in studying the vibrational modes of molecules and
|

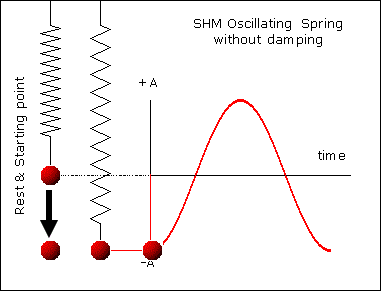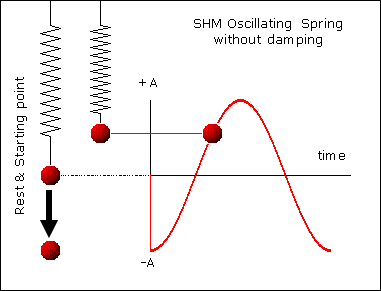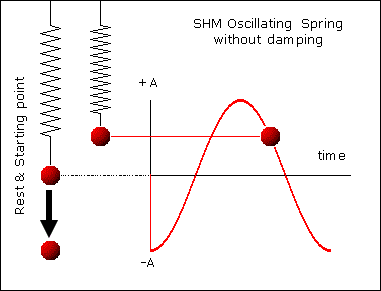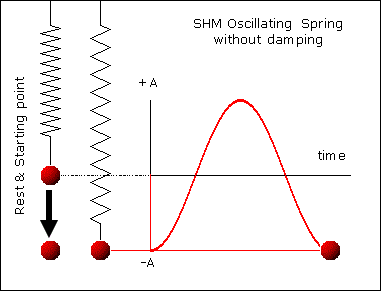

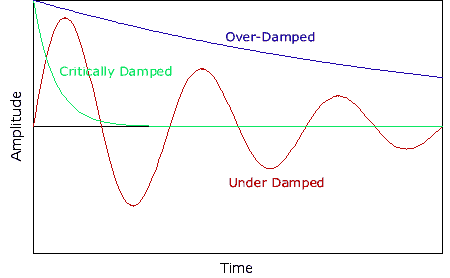
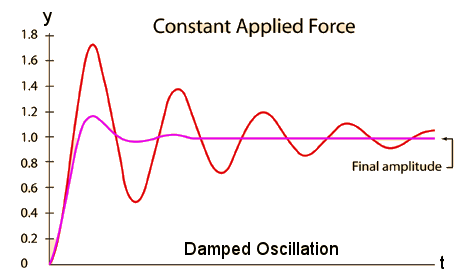

 , kd has unit sec-1.
, kd has unit sec-1. ) / {R2+[
) / {R2+[ 0,
0,  . This is known as resonant circuit, or tank circuit, or tuned circuit used in radio receiver.
. This is known as resonant circuit, or tank circuit, or tuned circuit used in radio receiver.



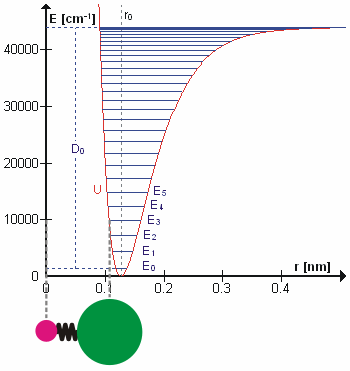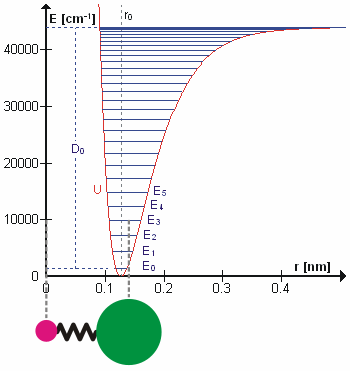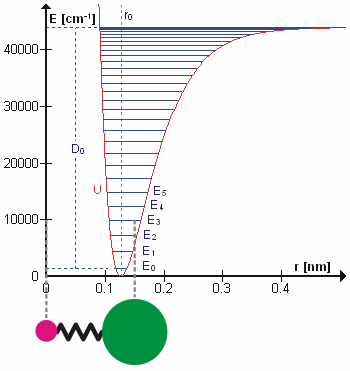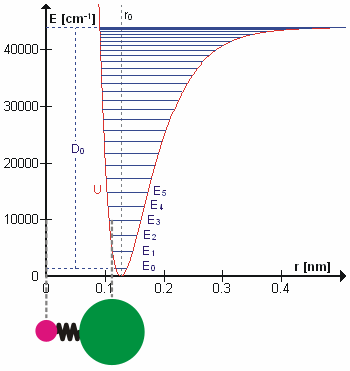



 d/dx, and
d/dx, and  n = En
n = En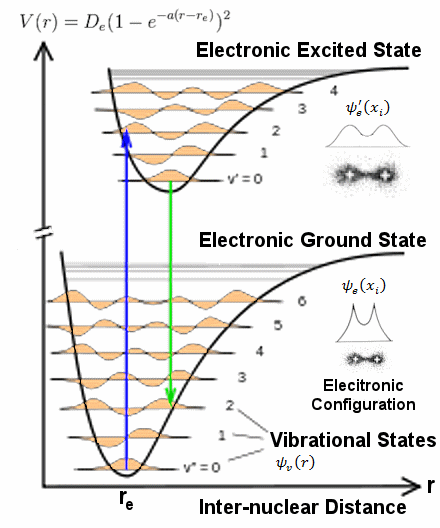





 can be switched between each other in terms of the
can be switched between each other in terms of the 

 =
= 

 (x-y)
(x-y) (k1)a
(k1)a