 |
the pi meson into an electron-positron pair (Figure 02). Since the spin for the pi meson is 0, the spin for the electron-positron pair must be opposite according to the conservation of angular momentum. Therefore, no matter how far apart are the members of this pair, if the spin is flipped for one of the member, the spin for the other member will also be flipped to the opposite at precisely the same moment. This non-local influence (objects can influence each other only locally according to classical physics) occur instantaneously, as if some form of communication, which Einstein called a "spooky action at a distance", operates not just faster than the speed of light, but infinitely fast.
|

 p
p q >
q >  ; it also violates the principle of locality (signal cannot travels faster than the speed of light) in special relativity (see Figure 01). They argued that "elements of reality" such as momentum and position are deterministic properties of particles although it is hidden in quantum theory which endows them with probability only. Hence quantum theory is an incomplete theory, there is no need to invoke "non-locality" and also can do away with the "uncertainty principle" if the hidden cause is included in the theory.
; it also violates the principle of locality (signal cannot travels faster than the speed of light) in special relativity (see Figure 01). They argued that "elements of reality" such as momentum and position are deterministic properties of particles although it is hidden in quantum theory which endows them with probability only. Hence quantum theory is an incomplete theory, there is no need to invoke "non-locality" and also can do away with the "uncertainty principle" if the hidden cause is included in the theory.

 1 and
1 and  (
( = (|x,x
= (|x,x
 ) = P--(
) = P--( b denotes the angle between the analysers I and II.
b denotes the angle between the analysers I and II.
 ----- (5)
----- (5)
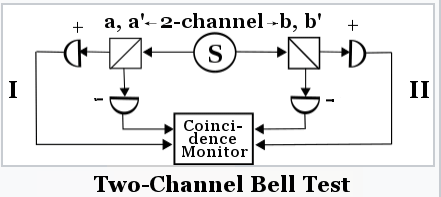
 SEPR(a,a',b,b')
SEPR(a,a',b,b')  Bell's Inequality ----- (7)
Bell's Inequality ----- (7) 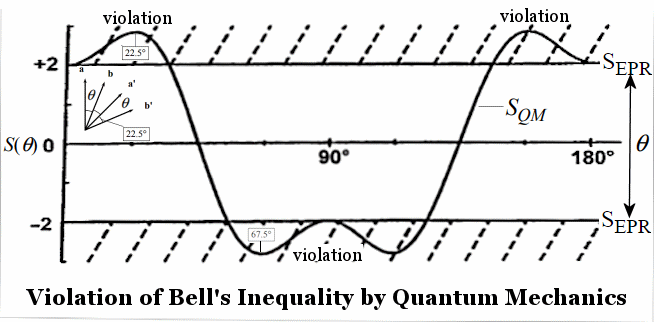
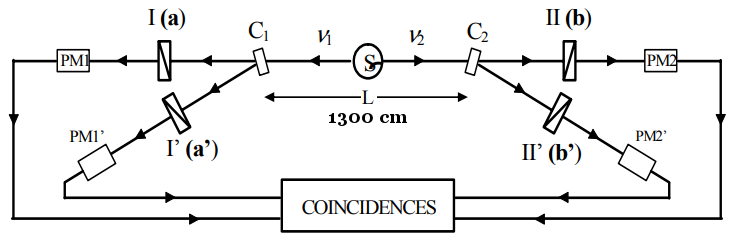

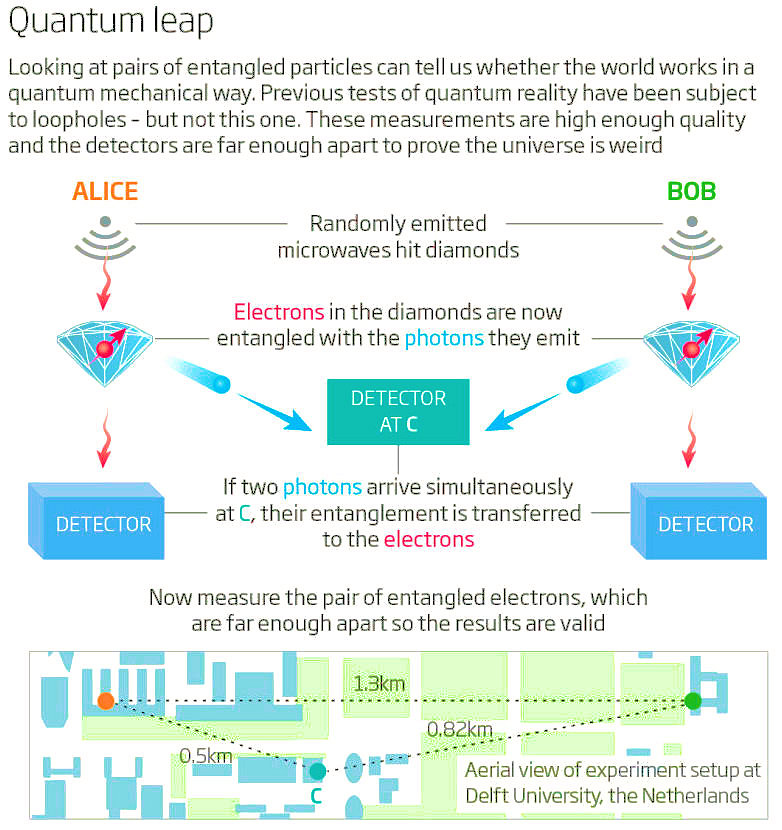

 .
.