

| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
 |
There is another level of quantum theory over the particle and wave as mentioned on "1st Quantization". In the Standard Model (SM) of elementary particles, it is the quantum fields that are ubiquitous in the formulation. In contrary to the classical fields such as the electro-magnetic fields in Maxwell's equations and the metric tensors in General Relativity, in which there is always a source such as charge and current or mass-energy tensor to generate the fields, the quantum fields in SM has no source - it is assumed to be everywhere and at all time in this Universe. |
Figure 01 Quantum Fields [view large image] |
Figure 02 Virtual Particles [view large image] |
That's why there is always a suspicion about an even deeper level to describe the detail of their origin. See "Quantum Fields and Vacuum Energy Density" for more on vacuum state. |
 |
 |
vacuum, all its energy was converted to the particles in this world. Since then, there is the Higgs field, which also existed in false vacuum state and then settled down to the true vacuum level of 125 Gev above the zero point energy. It permeats throughout the universe uniformly and isotropically, and endows mass to other particles. The interactions between the particles and the Higgs maintain a meta-stable state which could end anytime according to one calculation (see "Stability of the Universe"). |
Figure 03a The 24 Quantum Fields |
Figure 03b Elementary Interaction [view large image] |
Figure 03a lists the 24 elementary particles (or quantum fields) in the Standard Model (should add the Higgs hoson discovered in 2012), while Figure 03b specifies the kinds of interactions by these particles. |
 |
There are 12 fermion and 12 boson fields in the Standard Model (Figure 03a). The Lagranian L for leptons is shown in Figure 04. It contains all the lepton fields (waves) and the interactions between these fermions and bosons. The Lagranian L1 contains 1 EM , 2 weak boson fields; L2 has 6 leptonic fermion fields; L3 is for the Higgs boson. At this level, we are dealing with waves excited from the underlaying fields, i.e., one step up from the more or less featureless elements (see Figure 01). The interaction is expressed in the covariant derivative D  . There are altogether 3 coupling constants - g and g' are associated with the interaction between the gauge bosons W . There are altogether 3 coupling constants - g and g' are associated with the interaction between the gauge bosons W and B and B and the Higgs respectively, Ge is the Yukawa coupling constant, which defines the interaction between the Higgs and the lepton. The first three terms in Eq.(41c) are responsible for generating the mass of the gauge bosons, while the last term takes care of the fermion mass. and the Higgs respectively, Ge is the Yukawa coupling constant, which defines the interaction between the Higgs and the lepton. The first three terms in Eq.(41c) are responsible for generating the mass of the gauge bosons, while the last term takes care of the fermion mass. |
Figure 04 Lepton Lagranian for WS Model of SM [view large image] |
The quarks have a slightly different form of the Lagrangians by the title of quantum chromodynamics (QCD). |
 |
 |
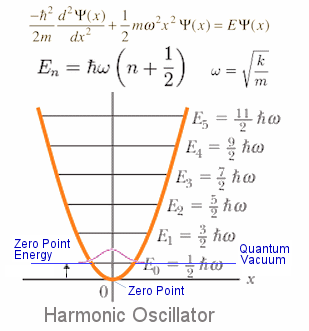
Similar to the harmonic oscillator, each of these quantum fields has a zero point energy causing infinity in theoretical calculation. It is subtracted from the total by moving the zero point up as shown in Figure 04b. The energy density at the zero point level should be a constant and is often assumed to be the dark energy which accelerlates the cosmic expansion and becomes important in the recent epoch. The total is about 10-8 ergs/cm3 or 10-29 gm/cm3 (Figure 04c). |
Figure 04b Zero Point Energy |
Figure 04c Dark Energy Density |


 = 1. It is supposed to simplify the notation of the formulas. It changes the unit of time to (3x1010) cm or to 1/(1.054x10-27erg), then the unit of the momentum, energy and mass becomes the inverse of length, while the charge, velocity, and angular momentum are dimensionless. The original value of c and
= 1. It is supposed to simplify the notation of the formulas. It changes the unit of time to (3x1010) cm or to 1/(1.054x10-27erg), then the unit of the momentum, energy and mass becomes the inverse of length, while the charge, velocity, and angular momentum are dimensionless. The original value of c and  can always be re-introduced by dimensional consideration (see more in Natural Units). Actually, the previous formulas are in natural units already.
can always be re-introduced by dimensional consideration (see more in Natural Units). Actually, the previous formulas are in natural units already.  (x) = A e-i(
(x) = A e-i( t-kx) ---------- (5),
t-kx) ---------- (5), = E, k = p, and E2 = k2 + m2, which is the relativistic version of the energy of a free particle.
= E, k = p, and E2 = k2 + m2, which is the relativistic version of the energy of a free particle.
 |
If a number operator Nk = ck ck is defined such that it operates on the state vector |nk ck is defined such that it operates on the state vector |nk to generate: to generate:Nk|nk  = nk|nk = nk|nk where nk is the number of particles in the k state; it follows that ck  |nk |nk = (nk+1)1/2|nk+1 = (nk+1)1/2|nk+1 ck|nk  = nk1/2|nk-1 = nk1/2|nk-1 Thus ck  increases the number of particles in the k state by 1, while ck reduces the number of particles in the k state by 1. They are called creation and annihilation operator respectively. The complete set of eigenvectors is given by: increases the number of particles in the k state by 1, while ck reduces the number of particles in the k state by 1. They are called creation and annihilation operator respectively. The complete set of eigenvectors is given by:
| |||
Figure 05 Hilbert Space [view large image] |
|
 | ---------- (9) |
 .
. represents the state of the system with each matrix element stands for vacuum (0 # of particle state), 1, 2, ... particles and so on. The 0 and 1 denote unoccupied and occupied respectively. The example above shows the 2 particles state is occupied.
represents the state of the system with each matrix element stands for vacuum (0 # of particle state), 1, 2, ... particles and so on. The 0 and 1 denote unoccupied and occupied respectively. The example above shows the 2 particles state is occupied. ck'
ck' |0
|0 = |1(k),1(k')
= |1(k),1(k') = ck'
= ck' ck
ck |0
|0 = |1(k'),1(k)
= |1(k'),1(k) ---------- (10a)
---------- (10a) ck
ck |0
|0 = |2(k)
= |2(k) ---------- (10b)
---------- (10b) , and kx =
, and kx =  t - kx) :
t - kx) :
 (x) =
(x) = 
 (x) indicateing that it really has no complex component.
(x) indicateing that it really has no complex component.
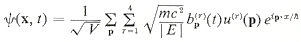 | ---------- (12) |
 | ---------- (13) |
 )ij = (b*)ji, the b's assume the same role as the c's except that the state vector |
)ij = (b*)ji, the b's assume the same role as the c's except that the state vector |  can have only 0 or 1 particle for a given state (p, r). For example, exchange of states for two particles produces a minus sign in the state vector :
can have only 0 or 1 particle for a given state (p, r). For example, exchange of states for two particles produces a minus sign in the state vector :  bp'
bp' |0
|0 = |1(p),1(p')
= |1(p),1(p') = -bp'
= -bp' bp
bp |0
|0 = -|1(p'),1(p)
= -|1(p'),1(p) ---------- (14)
---------- (14) bp
bp |0
|0 = |2(p)
= |2(p) = -bp
= -bp bp
bp |0
|0 = -|2(p)
= -|2(p) ---------- (15a)
---------- (15a) = 0. Thus, 2 spin 1/2 particles cannot occupy the same state - a characteristics of Fermi-Dirac statistics.
= 0. Thus, 2 spin 1/2 particles cannot occupy the same state - a characteristics of Fermi-Dirac statistics. operators, the probability density can now be re-defined as charge density. The total charge operator is in the form :
operators, the probability density can now be re-defined as charge density. The total charge operator is in the form : | ---------- (15b) |
 )".
)". |

|
Figure 06 Green's Function [view large image] |
G(x-x') is called the Green's function. It is the solution of Eq.(18) at the point source + free field otherwise. It is very useful in QFT. |
 |
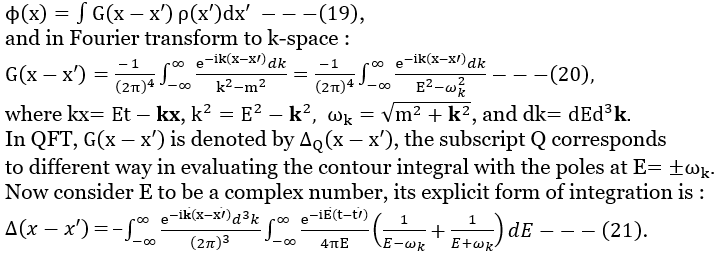
|
Figure 07 Contour Integral |
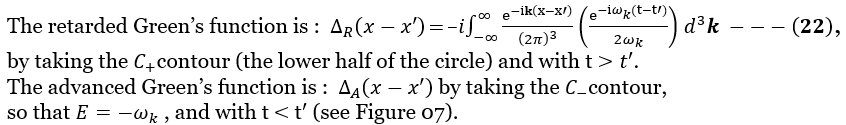
|
 F =
F =  R +
R +  A to take care of both particle and anti-particle respectively. Thus, :
A to take care of both particle and anti-particle respectively. Thus, :
 |

|
Figure 08 Feynman Diagram |
 |

 p1,
p1,  'p2,
'p2,  *p3,
*p3,  '*p4), plus other factors to be added later.
'*p4), plus other factors to be added later. (k - p1 + p3), or
(k - p1 + p3), or  (k + p2 - p4) for the vertex x or x'.
(k + p2 - p4) for the vertex x or x'. F(k) for the internal line. It represents the virtual bosons for all values of the 4-momentum k.
F(k) for the internal line. It represents the virtual bosons for all values of the 4-momentum k.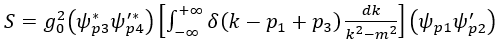
 |
S = [(M/V)2(E1E3E'2E'4)-1/2]  ( ( *p3 *p3 '*p4) {(g02)/[(p1 - p3)2 - m2]} ( '*p4) {(g02)/[(p1 - p3)2 - m2]} ( p1 p1 'p2) 'p2) ----- (29), ----- (29),where M and Eps are the mass and energy of the fermions, V is the normalization volume. |
Figure 09 Feynman and Friends [view large image] |
 to apply. It is partially resolved by "Perturbation Theory" which is applicable for small coupling constant such as in Quantum Electro-Dynamics (QED). It involves the separation of the interaction from the system by the assumption that the free field case is "nearly" valid requiring only minor corrections.
to apply. It is partially resolved by "Perturbation Theory" which is applicable for small coupling constant such as in Quantum Electro-Dynamics (QED). It involves the separation of the interaction from the system by the assumption that the free field case is "nearly" valid requiring only minor corrections. |
Figure 10a shows the Feynman diagrams corresponding to each term of the S-matrix expansion. The order number in S(n) is determined by the number of power in the coupling constant.
|
| Figure 10a Higher Order Feynman Graphs [view large image] |

 f|S|i
f|S|i is computed with the free field state vector |n
is computed with the free field state vector |n between the initial state (i) at t0 = -
between the initial state (i) at t0 = - and the final state (f) state at tn = +
and the final state (f) state at tn = + . The approximation would be getting progressively more accurate for small coupling constant as more terms are taken. Usually, one initial state can produce one or more final states as shown in Figure 10b, where three different initial states are taken as examples - namely, the electron positron scattering, the Compton scattering and the deep inelastic scattering. Each of this process produces many final states, but only a few have been shown just for illustration purpose. The Sfi is a complex number in general. It is called probability amplitude and is related to the probability of going from the i to f states. It has to satisfy the unitary condition, i.e.,
. The approximation would be getting progressively more accurate for small coupling constant as more terms are taken. Usually, one initial state can produce one or more final states as shown in Figure 10b, where three different initial states are taken as examples - namely, the electron positron scattering, the Compton scattering and the deep inelastic scattering. Each of this process produces many final states, but only a few have been shown just for illustration purpose. The Sfi is a complex number in general. It is called probability amplitude and is related to the probability of going from the i to f states. It has to satisfy the unitary condition, i.e.,
 |
 f (Sfi)*Sfi = 1, which guarantees that probability is conserved in the process. Such relationship indicates that the matrix Sfi has an inverse, which in turn implies that it is possible to return to the initial state from the final state at least in principle although the probability is almost zero in practice so that the second law of thermodynamics is "almost" never violated. This property is also related to the conservation of information, which caused so much trouble for Stephen Hawking. f (Sfi)*Sfi = 1, which guarantees that probability is conserved in the process. Such relationship indicates that the matrix Sfi has an inverse, which in turn implies that it is possible to return to the initial state from the final state at least in principle although the probability is almost zero in practice so that the second law of thermodynamics is "almost" never violated. This property is also related to the conservation of information, which caused so much trouble for Stephen Hawking.
|
Figure 10b S-Matrix Elements |
Note: For example in the electron positron scattering process, there are three possible finally states as illustrated in Figure 10b. The sum of the probabilities for each one of these has to be: S*11S11 + S*21S21 + S*31S31 = 1 to insure the unitary condition. |
 /c3)1/2 = 1.62x10-33 cm.
/c3)1/2 = 1.62x10-33 cm. /c5)1/2 = 5.39x10-44 sec.
/c5)1/2 = 5.39x10-44 sec.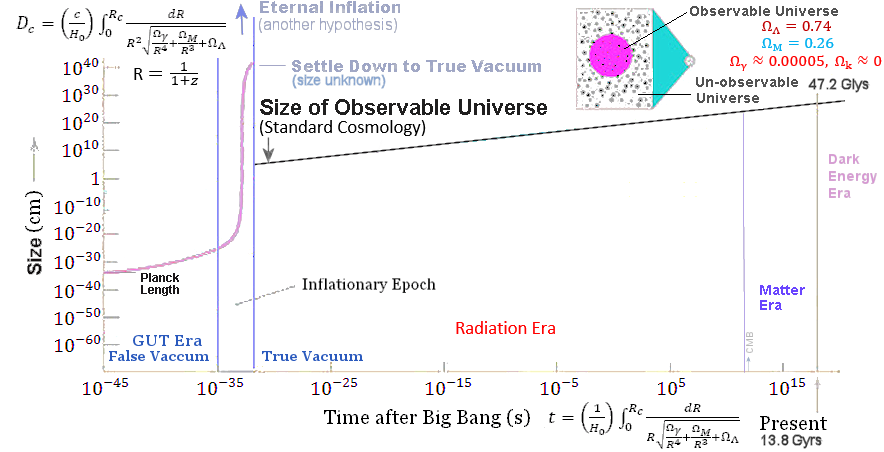 |
 |
|
Figure 11 Modern Cosmology |
Figure 12 |
The Planck Era is the period before the Planck time of 5x10-44 sec. Not much is known; nevertheless, Quantum Gravity offers some haphazard guessing about this world of so-called "Realm of Planck Scale". |
 t
t  tPL and
tPL and  x
x  LPL (for the corresponding Planck mass/energy) rendering it meaningless (see "What Is The Smallest Possible Distance In The Universe?").
LPL (for the corresponding Planck mass/energy) rendering it meaningless (see "What Is The Smallest Possible Distance In The Universe?").
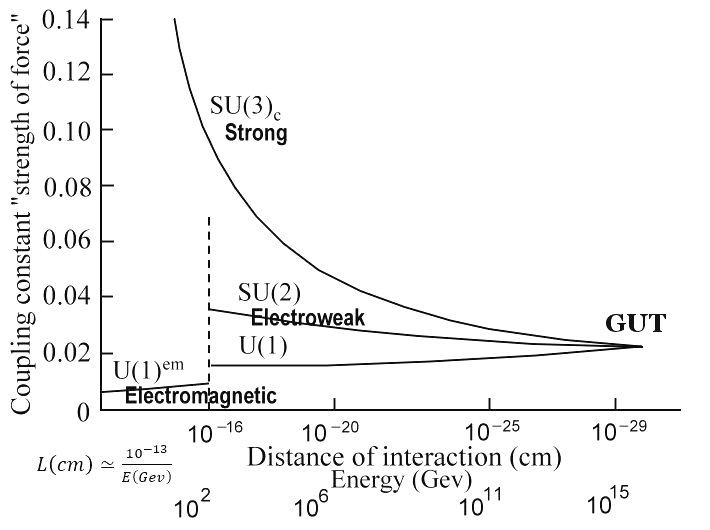 |
According to the "Theory of Cosmic Inflation", there was an inflaton field in a state of false vacuum (Figure 13b) during this period. Also in co-existence were the gravitational field and one unified field (for the strong and electro-weak interactions, Figure 12). The Grand Unified Theory suggests that at energies above 1015 Gev, all gauge bosons can be produced freely and all interactions have the same strength (Figure 13a). The quarks can change color charges, as easily as transform into leptons (hence the proton decay, which failed to be confirmed experimentally leading to the desertion of the theory). |
Figure 13a GUT |
See "Higgs Field, the Eternal and Ubiquitous (2021 Edition)" |
 |
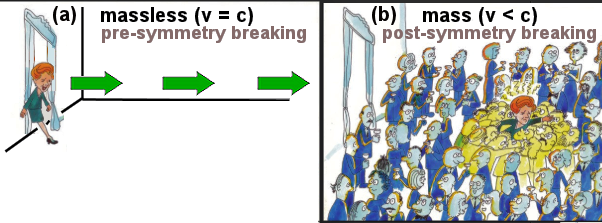
  In early universe up to 10-12 sec after BB, the fermions (u,d,s,c,b,t) are restmass-less, i.e., mi = 0. They couple to the SU(3) Gauge bosons Ga, (where the index "a" runs from 1 to 8) as well as the SU(2) Gauge bosons according to the Standard Model (see Figure 14). The system of quarks and gluons flew at the speed of light as some sort of fluid. This state of the QCD can be considered as free relativistic gas called Quark-Gluon Plasma (QGP, see "Quark-Gluon Plasma and the Early Universe"). |
Figure 13b Inflation |
[view large image] |
 |
 |
|
Figure 14 SM, Parameters |
Figure 15 Mass, Origin of |
Higgs field decay from its false vacuum state to the true vacuum endowing restmass to most particles. Before this event they all move at the speed of light (Figures 14, 15). |
 |
 |
Figure 16 Stability of the Universe [view large image] |
and the sum is over all SM particles acquiring a Higgs-dependent mass Mi. The precise form of V1 is not important in the present context, it just shows that the Higgs potential also depends on the particles it acts upon. Furthermore, only the heaviest top quark in the sum is retained in the following consideration. |