| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
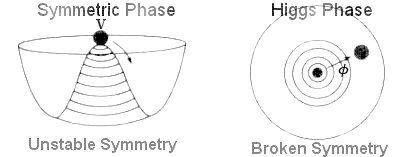
The existence of asymmetric solutions to a symmetric theory is common to many branches of physics. The reason lies in the fact that the symmetric state is not the state of minimum energy, i.e., the ground state, and that in the process of evolving towards the ground state, the intrinsic symmetry of the system has been broken. Figure 01 shows that the initial position of the marble on top of the bump is symmetric but not in a |
Figure 01 Symmetry Breaking |
state of minimum energy. A small perturbation will cause the rotational symmetry to be broken and the system to assume a stable state configuration. When the symmetry of a physical system is broken in this way, it is often referred to as "spontaneous symmetry breaking (SSB)". |
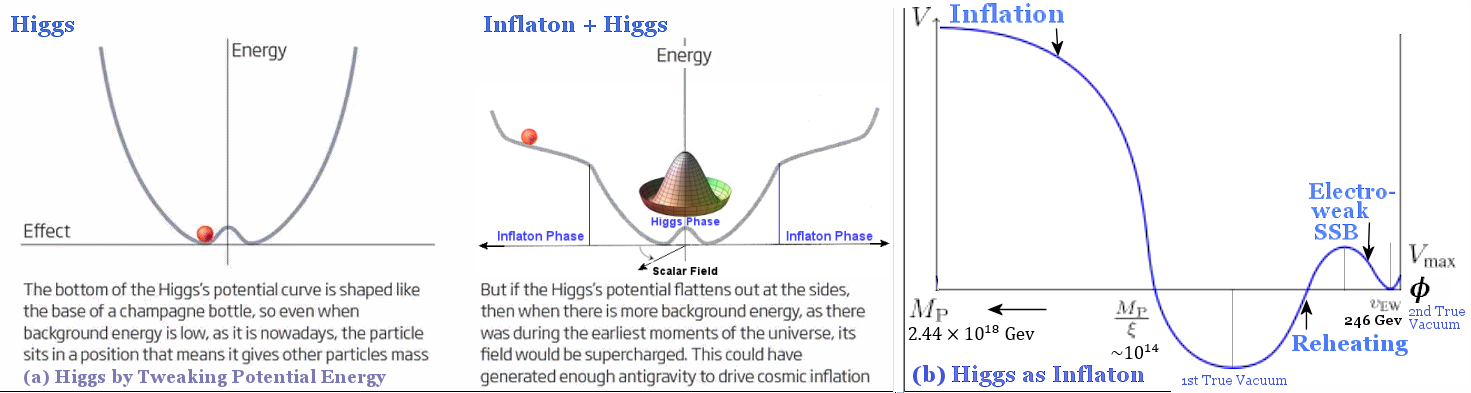 |
The obvious omission in this model is the absence of the reheating process which is responsible for the generation of matter at the end of inflation (see "Inflation Era"). According to another model developed in 2014 (see "Inflation, LHC and the Higgs boson"), it is indeed possible to produce a potential V with an inflationary plateau at large values of the scalar field, and two minima (Figure 04,b). |
Figure 04 Higgs as Inflaton |
A much simplified version of the mathematic derivation is sketched below to illustrate the theoretical formulation. |
 = (-g)1/2R ---------- (1)
= (-g)1/2R ---------- (1)

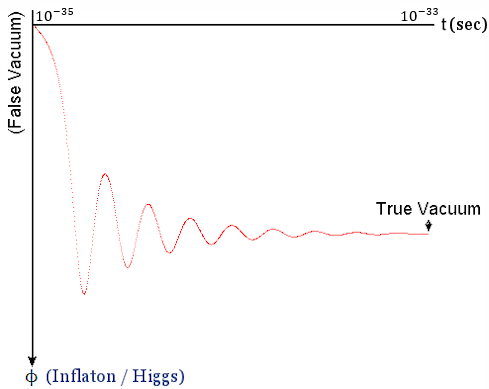 |
 . It is also possible to get some idea about each stage of the evolution by inspecting dv/d . It is also possible to get some idea about each stage of the evolution by inspecting dv/d in Figure 04,b : in Figure 04,b :
|
Figure 05 Higgs/Inflaton, Evolution with Time |
 |
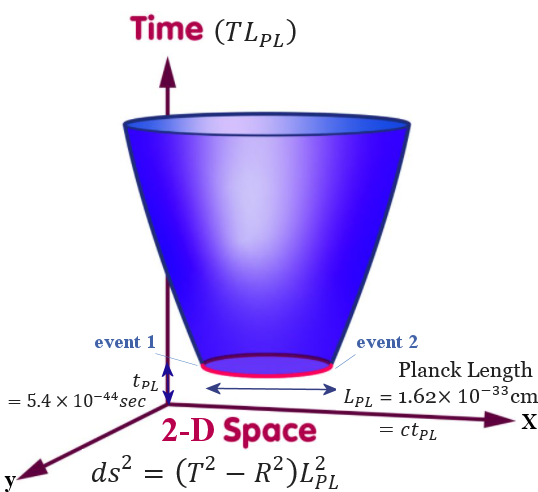
Since inflation occurred at the beginning of the Universe, it is expected that all branches of physics would be combined at this point in a domain called Quantum Gravity (Figure 05a). It would include the gravitational constant G associated with gravity, the Planck constant  for quantum, and the velocity of light c in special relativity. All these are encompassed in the system of Planck scale with Planck length LPL = (G for quantum, and the velocity of light c in special relativity. All these are encompassed in the system of Planck scale with Planck length LPL = (G /c3)1/2 = 1.62x10-33 cm, Planck time tPL = (G /c3)1/2 = 1.62x10-33 cm, Planck time tPL = (G /c5)1/2 = 5.39x10-44 sec, Planck mass MPL = ( /c5)1/2 = 5.39x10-44 sec, Planck mass MPL = ( c/G)1/2 = 2.17x10-5 gm, and Planck energy EPL = ( c/G)1/2 = 2.17x10-5 gm, and Planck energy EPL = ( c5/G)1/2 = 1.22x1019 Gev (see "Realm of Planck Scale"). c5/G)1/2 = 1.22x1019 Gev (see "Realm of Planck Scale"). That's why the initial system is postulated to be in such scale at the beginning the Universe. |
Figure 05a Quantum Gravity |
In addition, LPL and tPL are the absolute minimum space, time. Because any scale below such limit violates the uncertainty principle. For example, EPL t t   , since EPLtPL = , since EPLtPL =  , hence , hence  t t  tPL; similarly for tPL; similarly for  x x  LPL.
(see "What Is The Smallest Possible Distance In The Universe?"). LPL.
(see "What Is The Smallest Possible Distance In The Universe?").
|
 |

|
Figure 05b Semi-classical Model [view large image] |
According to the consensus view on cosmic inflation, the duration and expanse during that period are : T ~ c(10-32/10-44) ~ 1022, R ~ (10-6/10-33) ~ 1027 and T = R =1, ds2 = 0  time-like in the beginning. time-like in the beginning.Thus, R >> T and ds2 < 0 thereafter, such events are qualified as "Inflation" - QED. |
 c/G)½ = 2.17x10-5gm, its corresponding Schwarzschild Radius rs is equal to twice the Planck length, i.e., rs = 2GMPL/c2 = 2LPL implying that the initial radius is inside the event horizon, i.e., such Planck scale particle is a black hole. It has been shown that such black hole would evaporate in time interval :
c/G)½ = 2.17x10-5gm, its corresponding Schwarzschild Radius rs is equal to twice the Planck length, i.e., rs = 2GMPL/c2 = 2LPL implying that the initial radius is inside the event horizon, i.e., such Planck scale particle is a black hole. It has been shown that such black hole would evaporate in time interval : G
G R2 / 3 = - kc2.
R2 / 3 = - kc2. |
There are many attempts to add quantum into gravity over the course of many decades usually under the umbrella of "Theories Of Everything (TOE)" (see Figure 05c). The "semi-classical, and further ... here", adds one more version into the many alternates. It suggests a rule for quantization (see "Novel Higgs Field"), has no problems with the cosmological constraints, offers an explanation for the dark energy, and is in agreement with the latest measurement of CMB polarization. |
Figure 05c Theories Of Everythibg (TOE) |
Anyway, there is yet another way to achieve the merger by adding gravity to quantum (see "Newtonian Quantum Gravity, 1995", "Newtonian Quantum Gravity, 2006" and Figure 05a). |
 |
There is an alternate way to associate the Higgs quantum field with cosmic inflation. The formulation starts from a very small universe at Planck scale with Mass/Energy M = MPL and size LPL. Accordingly, its energy density  PL ~ 10114 erg/cm3. Such entity is at the realm of quantum gravity. Unfortunately, there is no universally acceptable theory for performing the qunatization of gravity now. One of the ad hoc solutions is to quantize the Friedmann Equation for cosmic expansion. Mathematically, the procedure transforms a non-linear equation such as Eq(5) into a linear equation such as Eq.(6). That is, the procedure displays a continuous scaffolding sheet as divisible units by examining the thing closely (see Figure 05d). PL ~ 10114 erg/cm3. Such entity is at the realm of quantum gravity. Unfortunately, there is no universally acceptable theory for performing the qunatization of gravity now. One of the ad hoc solutions is to quantize the Friedmann Equation for cosmic expansion. Mathematically, the procedure transforms a non-linear equation such as Eq(5) into a linear equation such as Eq.(6). That is, the procedure displays a continuous scaffolding sheet as divisible units by examining the thing closely (see Figure 05d).
|
Figure 05d Scaffolding Sheet as QG |
 G
G R2 / 3 = - kc2.
R2 / 3 = - kc2. = MPL/[(4
= MPL/[(4 /3)R3(LPL)3], it becomes :
/3)R3(LPL)3], it becomes : (tPL)2] = -kc2 ---------- (5),
(tPL)2] = -kc2 ---------- (5),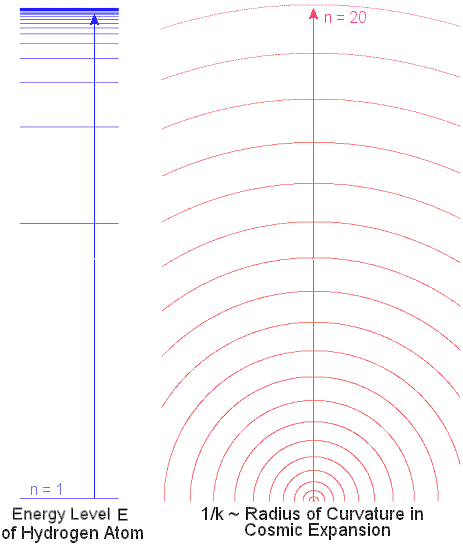 |
 |
Figure 06 H Atom Energy Level & Cosmic Radius |
Now the hydrogenic wave function  n(R) can be identified to the inflaton field (or the Higgs field n(R) can be identified to the inflaton field (or the Higgs field  , or whatever designation). Inflation corresponds to the transition from the level of n , or whatever designation). Inflation corresponds to the transition from the level of n  1 to the continuum (n 1 to the continuum (n   ). Energy should be infused to pump the transition as shown in Figure 07. After inflation, the ). Energy should be infused to pump the transition as shown in Figure 07. After inflation, the |
 0. The gravity couples only to mass/energy, and detached from the Higgs field.
0. The gravity couples only to mass/energy, and detached from the Higgs field. |
 |
Effort to formulate theory in time or size smaller than the Planck scale (~10-44 sec, Figure 08) is doomed to fail as any system below such limit violates the uncertainty principle of  t t  tPL (for the corresponding Planck mass/energy, i.e., EPL tPL (for the corresponding Planck mass/energy, i.e., EPL t t   = EPLtPL) and = EPLtPL) and  x x  LPL rendering it meaningless (see "What Is The Smallest Possible Distance In The Universe?"). LPL rendering it meaningless (see "What Is The Smallest Possible Distance In The Universe?").
|
Figure 07 Cosmic Energy Density [view large image] |
Figure 08 |
BTW, the cosmic evolution in Figure 08 shows that the structures in quantum domain had completed within a very short time interval about 10-32 sec. Then it went through a period of making the atoms for building the large structures, |
 or
or  in term of energy density (the so-called Dark Energy).
in term of energy density (the so-called Dark Energy). R2 c2 / 3 ---------- (8a)
R2 c2 / 3 ---------- (8a) is the cosmological constant. It can be reduced to a form adopted by the Steady State Theory as :
is the cosmological constant. It can be reduced to a form adopted by the Steady State Theory as : c2/3)1/2 is the Hubble constant in the Steady State Theory.
c2/3)1/2 is the Hubble constant in the Steady State Theory. , i.e., Eq.(8b) becomes :
, i.e., Eq.(8b) becomes : 
 |

|
Figure 08b Dark Energy [view large image] |

|
 |
Meanwhile the quantum fields are also homogeneous, isotropic, and constant over the eon; it is tempting to identify each of the 24 quantum fields (Figure 08b2) to the eigen-function  with different value of H (labeled by with different value of H (labeled by  n, Hn and n, Hn and  n for n = 1, 2, 3, ... 24). It is estimated that they would have energy density n for n = 1, 2, 3, ... 24). It is estimated that they would have energy density   10-8 erg/cm3, with the corresponding vacuum (zero point) energy En = h 10-8 erg/cm3, with the corresponding vacuum (zero point) energy En = h n/2, where n/2, where  n = (k/m)1/2, m is the mass, k the spring constant for the nth particle. The elementary particles in this world are just in the excited state of the quantum fields. As the Universe expands, the quantum fields have to be replenished similarly to the dark energy. n = (k/m)1/2, m is the mass, k the spring constant for the nth particle. The elementary particles in this world are just in the excited state of the quantum fields. As the Universe expands, the quantum fields have to be replenished similarly to the dark energy.
|
Figure 08b2 Quantum Fields |
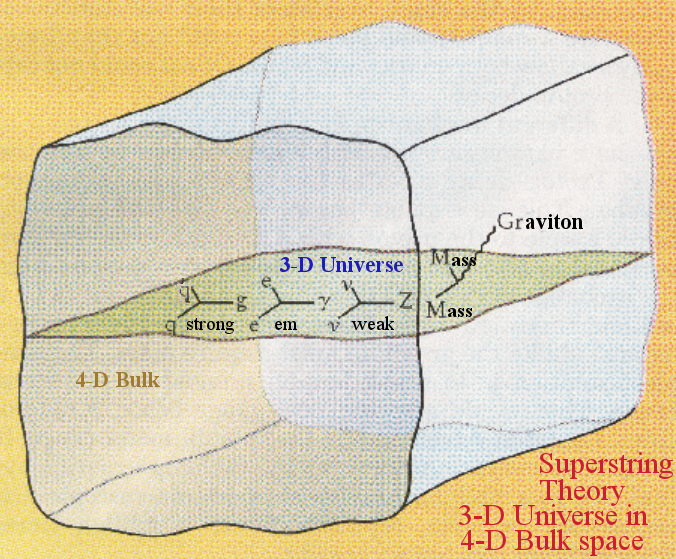 |
As for where does the infusing energy come from ? The quick answer would be from the 4th spatial dimension (Figure 08b3). The corollary for contraction to the beginning is to remove such energy back to the bulk. Thus, such reversal process would not end up with infinite matter-energy as oft-quoted in the past. Unfortunately, the "Superstring Theory" is not viable anymore due to failure of finding any experimental evidence. Or, is the bulk just "Another 3-D World" beyond this Universe ? |
Figure 08b3 |
This is part of the progress in science - more problems are created following the resolution of an old one. |
 |
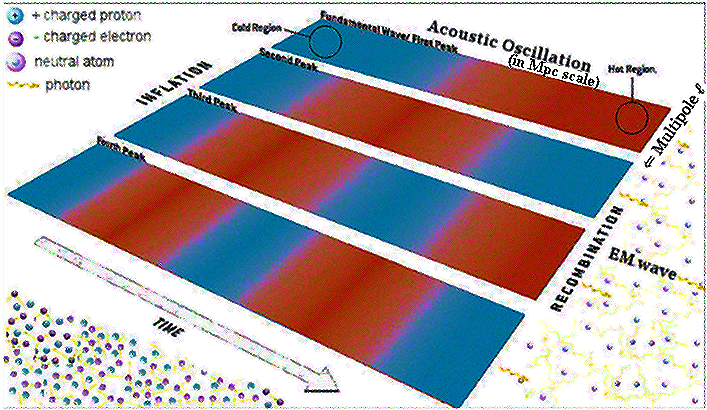
The pattern on Cosmic Microwave Background (CMB) has shown conclusively that it is the relic of density fluctuation. The theory of cosmic inflation is rather convincingly (not 100%) ascribed as the origin. Mathematically, the CMB (the earliest observable) is expressed by the Power Spectrum : Ps(k) = Ask(ns-1) ---------- (9), where k is the Fourier transform of the spatial coordinate x, ns  1 the scalar index, As the scalar amplitude, the subscript "s" denotes scalar type perturbation (quantum fluctuation), Ps(k) represents the density fluctuation in k-space corresponding to random fluctuation in x-space (see Figure 08c). 1 the scalar index, As the scalar amplitude, the subscript "s" denotes scalar type perturbation (quantum fluctuation), Ps(k) represents the density fluctuation in k-space corresponding to random fluctuation in x-space (see Figure 08c).
|
Figure 08c Primordial Fluctuations |
Some versions of the "Inflation Theory" also include the fluctuation in gravity (or metric tensor in General Relativity paradigm). It is often referred as primordial gravitational wave which is expressed as Pt(k) = Atknt ---------- (10), |

 , which in turn induced the density fluctuation
, which in turn induced the density fluctuation 
 .
.
 |
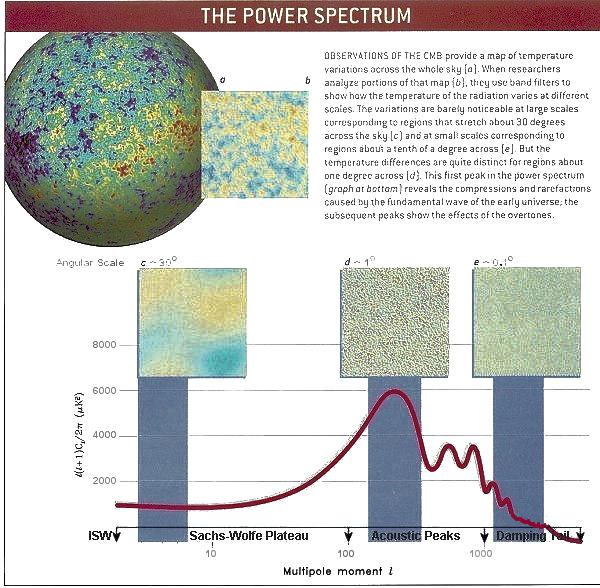 |
The gravitational attraction in the density enhanced regions, and the radiation repulsion acted together to produce the incoherent acoustic oscillations (noise). Compressing a gas heats it up; letting it expand cools it down - this is the origin of the temperature variation which eventually shows up as CMB. As shown in Figures 08d and 08e, the main peak is the oscillatory mode that went through 1/4 of a period (reaching maximal compression) at the time of recombination (between electrons and protons to form neutral atoms). The lower peaks correspond to the harmonic series of the main peak frequency. |
Figure 08d acoustic oscillations [view large image] |
Figure 08e Power Spectrum |
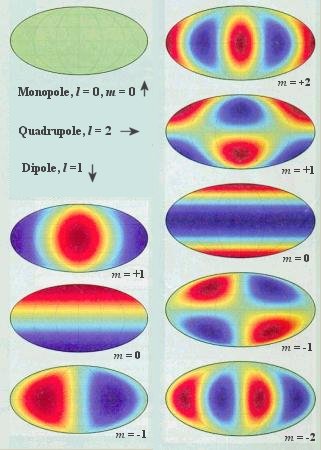 |
In angular coordinates, the temperature fluctuation is expressed mathematically by : where Y  m( m( , , ), is the Spherical Harmonics, and ), is the Spherical Harmonics, and  = 0 denotes the monopole, = 0 denotes the monopole,  = 1 the dipole, = 1 the dipole,  = 2 the quadrupole, ..., and m can be any integer between - = 2 the quadrupole, ..., and m can be any integer between - and and  . Each alm constitutes a multipole mode. The lowest multipoles are the largest-area, continent- and ocean-size undulations on the temperature map. Higher multipoles are like successively smaller-area plateaus, mountains and hills (trenches and valleys) inserted on top of the larger features. The entire complicated topography is the sum of the individual multipoles (Figure 08f). . Each alm constitutes a multipole mode. The lowest multipoles are the largest-area, continent- and ocean-size undulations on the temperature map. Higher multipoles are like successively smaller-area plateaus, mountains and hills (trenches and valleys) inserted on top of the larger features. The entire complicated topography is the sum of the individual multipoles (Figure 08f).
|
Figure 08f Multipole |
Eq.(11) is the Inverse Fourier Transform back to the x-space with integration replaced by summation over the multipole moment  , Ylm playing the role of eikx, and alm the power spectrum Ps(k) in Eq.(9). , Ylm playing the role of eikx, and alm the power spectrum Ps(k) in Eq.(9). |
 |
There are two distinct gravitational fluctuations corresponding to two kinds of polarizations as shown in Figure 08g. The E-mode is similar to the scalar fluctuation with  g g  for for  = =  = 1,2,3 producing compression/expansion perturbation. While the B-mode is for = 1,2,3 producing compression/expansion perturbation. While the B-mode is for    producing shear perturbation. producing shear perturbation.
|
Figure 08g Tensor Polarization [view large image] |
Thus, the scalar fluctuation generates only E-mode polarization; while the tensor fluctuation (gravitational wave) generates both E-mode and B-mode polarizations. |
 |
Polarization in CMB can be detected by using a polarizer (by the antenna in astronomical instrument). The corresponding formulas to Eq.(11) for CMB in E-mode and B-mode are : where E(n) and B(n) are CMB for the E-mode, and B-mode respectively, and n denotes the direction on the sky (see "Probing Inflation with CMB Polarization"). |
Figure 08h CMB Spectra, and Polarization Patterns |
Figure 08h,a shows the un-polarized, E-mode and B-mode CMB from both scalar and tensor perturbations (dotted curves). The B-mode by lensing is detected from only a small patch of the sky via gravitational lensing. Figure 08h,b shows the patterns around hot and cold spots. |
 |
 |
BICEP2's (Figure 08i) first attempt was a failure because it has not taken into account the inter-galactic dust (see "B-mode Detection, 2010's"). Since then it has created a precise inter-galactic model to subtract out the masking. The 2021 BICEP2 measurement provides the tightest constraint to gravitational perurbation with r < 0.036. The BICEP2 team have arrived at this limit by combining data at three frequencies (96 GHz, 150 GHz, 220 GHz) from their own experiment, complemented by archival data from the WMAP and Planck. |
Figure 08i BICEP2 Experiment [view large image] |
Figure 08j r-Ratio [view large image] |
Figure 08j plots the r-ratio r = Pt/Ps vs the scalar index ns. It encompasses the prediction of some Inflation Models, and experimental measurement (current and future). It is related to the e-fold expansion of space during inflation and is |
 n(Lf/Li), where L is the size of the universe for the initial (i) and final (f) state of the inflation. To be consistent with the theory of inflation, the value of N has to be between 40 and 60 (to solve the cosmological problems and to be in agreement with the measurement of ns respectively).
n(Lf/Li), where L is the size of the universe for the initial (i) and final (f) state of the inflation. To be consistent with the theory of inflation, the value of N has to be between 40 and 60 (to solve the cosmological problems and to be in agreement with the measurement of ns respectively). is identified to the Higgs quantum field, which would fluctuated according to the uncertainty principle (see Figure 08k). The fluctuation would in turn produce variation in energy, which can be equated to
is identified to the Higgs quantum field, which would fluctuated according to the uncertainty principle (see Figure 08k). The fluctuation would in turn produce variation in energy, which can be equated to 
 in the conventional theory of of inflation. Thus, the formulation of the CMB via the variation of
in the conventional theory of of inflation. Thus, the formulation of the CMB via the variation of  would be the same as the case of the variation of the "inflaton" field in the conventional theory; particularly, ns
would be the same as the case of the variation of the "inflaton" field in the conventional theory; particularly, ns  1.
1. |
With such size at the end of the inflation, the total mass M = (10114/c2)(10-6)3 ~ 1075 gm, where the 10114 erg/cm3 is the constant energy density infusion during the period of inflation. This value of M is much greater than the mass of the observable universe ~ 1056 gm implying that the rest of the mass is in the un-observable part of the universe (see Figure 08l). |
Figure 08l Cosmic Expansion |
The boundary of the un-observable universe for the current epoch ruob can be estimated by : M ~ 1075 ~ 10-29(ruob)3, where 10-29 gm/cm3 is the current matter density, giving ruob ~ 1035 cm (see Figure 08l). |
 |
The Schwarzschild radius for M ~ 1075 gm is rs = 2GM/c2 ~ 1047 cm >> ruob indicating that our Universe could be a black hole if the density is concentrated into a much smaller region forming a compact mass. It doesn't seem to be the case by astronomical observations. Anyway, there could be "Another World" beyond ours rendering many cosmic events unfathomable (Figure 08l & ąD). Such possibility suggests that human beings are extremely unimportant in the grand scheme of the cosmos as portrayed in a 1985 movie called "Insignificance" in which Einstein and Monroe explore relativity and our place in the Universe (Figure 08m). |
Figure 08m Insignificance [view large image] |
  |
 rad = 8.24x10-5 implying that the curvature density parameter
rad = 8.24x10-5 implying that the curvature density parameter  k < 10-5. Since
k < 10-5. Since  k = kc2/(H0)2, for the Hubble constant H0 = 72 (km/sec)/Mpc,
k = kc2/(H0)2, for the Hubble constant H0 = 72 (km/sec)/Mpc, 1066 cm-2, it has diminished ~ 10128 fold during the period of inflation.
1066 cm-2, it has diminished ~ 10128 fold during the period of inflation.
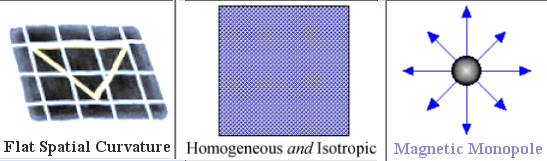 |
|
Figure 08n The 3 Problems [view large image] |
 |
Furthermore, Entropy is defined as the degree of randomness, which can be expressed alternatively as the degree of freedom in a system, i.e., the number of different parameters or arrangements needed to specify completely the state of a system. The evolution of entropy in the universe can be separated into four phases as described in Figure 08o, which shows lot of (???) for the very low entropy at the beginning of the universe. It has been a puzzling problem since a hot Big Bang should involve a lot of entropy (randomness/disorder). The mathematics in the above quantum cosmological model is specified by only "one" parameter, i.e., the Planck length LPL, which is the absolute minimum entropy for any system. Thus, low entropy came naturally in the model resolving the paradox. |
Figure 08o Evolution of Entropy [view large image] |
 |
The universe starts with gravity (which goes on by itself) and a quantum wave function that is identified as the Higgs field. This Higgs field went on to undergo many phase changes and finally settled down with 3 distinct quantum fields plus the Higgs field itself as shown in Figure 09. Such phenomena is similar to the phase transition of water (see Figure 02), which can exist in the form of gas, liquid, and solid in macroscopic states (similar to the strong, weak, and em quantum fields; or like mother and children). |
Figure 09 Quantum Field History (modified) [view large image] |
NB : The gravitational field is a classical field that does not follow the rules for the quantum fields. It only coupled to the Higgs field at the very early cosmic time in the form of quantum gravity. It detaches from the Higgs after inflation when the size of the universe is beyond the quantum domain. |
 |
|
Figure 09b Convergence of Quantum Gravity [view large image] |
Figure 09b shows all kinds of objects in this world with different size and mass. Ultimately, they all emerge from a tiny speck at the Planck scale via the action of Quantum Gravity (see the corresponding Table). |
 . The transition of
. The transition of  from the state of huge curvature k to k = 0 represents the period of inflation at the end of which it approaches an oscillatory form ~ Ae-i(
from the state of huge curvature k to k = 0 represents the period of inflation at the end of which it approaches an oscillatory form ~ Ae-i( t-kx), which is the solution for the "Klein-Gordon Equation of the Scalar Field". At this stage, the Higgs field could be the only quantum field around. It used to be called "Grand Unification" by assuming that all the quantum fields are in existence all the time but merged together at this point.
t-kx), which is the solution for the "Klein-Gordon Equation of the Scalar Field". At this stage, the Higgs field could be the only quantum field around. It used to be called "Grand Unification" by assuming that all the quantum fields are in existence all the time but merged together at this point. 0 in the quantum cosmological model.
0 in the quantum cosmological model.
 |
 ) to the Klein-Gordon Equation, see Eq.(3b)). ) to the Klein-Gordon Equation, see Eq.(3b)). |
Figure 10 Quark-Gluon Plasma [view large image] |
N.B. Reheating is not necessary, if the energy infusion is not from the immediate environment (see "Another World"). |
 |
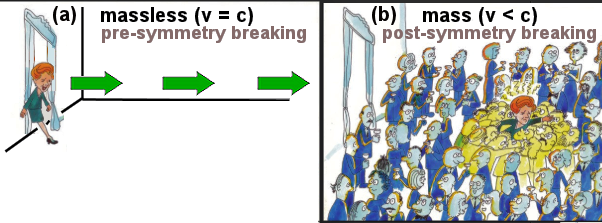 |
Higgs and hence the quantum particles (excited from the fields) are restmass-less moving at the velocity of light (Figure 12). Most of them acquired restmass only after SSB. The event separated the electroweak field into the electro-magnetic and weak; it also made the left/right-handed versions of the quarks and leptons acting differently in weak interaction. |
Figure 11 SM, Parameters |
Figure 12 Mass, Origin of |
Another phase change occurs about 10-5 sec after BB. This one transforms the Quark-Gluon Plasma to the bound state of Hadons (see "Chiral Symmetry Breaking"). |
 |
 |
Figure 13 Stability of the Universe [view large image] |
and the sum is over all SM particles acquiring a Higgs-dependent mass Mi. The precise form of V1 is not important in the present context, it just shows that the Higgs potential also depends on the particles it acts upon. Furthermore, only the heaviest top quark in the sum is retained in the following consideration. |
 |
The concept of gauge invariance (or gauge symmetry) can best be visualized with an example, which portrays a boat floating on the water surface with the depth of water at 3 meters (Figure 14). The gauge (the water level marker) at the left registers a reading of 6 meter on the surface and 3 meter on the bottom, while the measurements from the other one at the right are 9 and 6 meter correspondingly. The differences in the readings are the result of moving the right marker further down, but the depth of water remains the same at 3 meters - the picture has not been changed by moving the gauge around. In theorietical physics it is the governing equation that is unchanged (invariant) under the change of some parameters, which turn out to be the phase angles in an abstract space. When the system changes during the process of measurement, e.g., the boat sinks to the bottom during a storm, the symmetry is borken, i.e., it is not the same before the measurement. If it occurs naturally, then it is said to be Spontaneous Symmetry Breaking (SSB). |
Figure 14 [view large image] Gauge Invariance |
 |
In Gauge theory, the Largangian or field equation is invariant under the gauge transformation : ' = ei(a ' = ei(a t) t)  , ,where a is the phase angle associates with the "axis", t the generator in the form of nxn matrix, n the dimension of the Gauge space, the number of phase angles is determined by the formula Na = n2 - 1 (except for n = 1, Na = 1, see a little bit more in "Unitary Groups"). Figure 15 is an example of simplest Gauge transformation with n = 1. It shows that the SO(2) rotational transformation of 2-component field (interpreted as two +/- charge states) is equivalent to a single complex field in U(1)= ei  I (I = 1) Gauge group. In general SO(n+1) ~ SU(n), where "S" means that the transformation is "Special" with |det(U)| = +1, which implies continuous rotations without reflection. I (I = 1) Gauge group. In general SO(n+1) ~ SU(n), where "S" means that the transformation is "Special" with |det(U)| = +1, which implies continuous rotations without reflection.
|
Figure 15 [view large image] |
This is "Global Gauge Transformation" applicable to all space. It is the spatial dependence "Local Gauge Transformation" that generate the Gauge bosons responsible for interaction of particles. |
 ' = ei
' = ei
 , where
, where  is a constant, while the wave function is identified to the Higgs field up till the end of inflation.
is a constant, while the wave function is identified to the Higgs field up till the end of inflation. 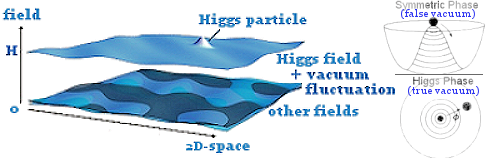 |
why, and when, but in certain circumstance (probably via decreasing temperature caused by cosmic expansion), the Higgs field would develop to a false vacuum state and then decays to the state of true vacuum H (as depicted in Figure 15b). Then the particles would interact with the Higgs field to slow down by exchange of energy and appear as acquiring mass. |
Figure 15b Higgs Field |
It is not known whether the quantum fields are inherent to the initial environment or developed gradually. Regardless of either possibility, one Gauge theory assumes that it started with a more encompassed Gauge group namely the SU(5) (also see "Group"). |
 |
about 10-35 sec after the Big Bang. These additional bosons carry new forces which can transform quarks into leptons and vice versa (hence the proton decay, which failed to be confirmed experimentally leading to the desertion of the theory). |
Figure 16 GUT, SU(5) |
Moreover, the theory also predicts the existence of magnetic monopole, which is also not observed in nature. See the more encampassing SO(10) Group. |
 2 +
2 + 
 4 (aka potential energy V), where the mass M > 0 and the self-coupling constant
4 (aka potential energy V), where the mass M > 0 and the self-coupling constant  > 0 (see Figure 17, upper right).
> 0 (see Figure 17, upper right). < 0). The Higgs becomes unstable after such transformation; it is said to be in "false vacuum".
< 0). The Higgs becomes unstable after such transformation; it is said to be in "false vacuum".  ). This is the link between SSB and ESB since such
). This is the link between SSB and ESB since such
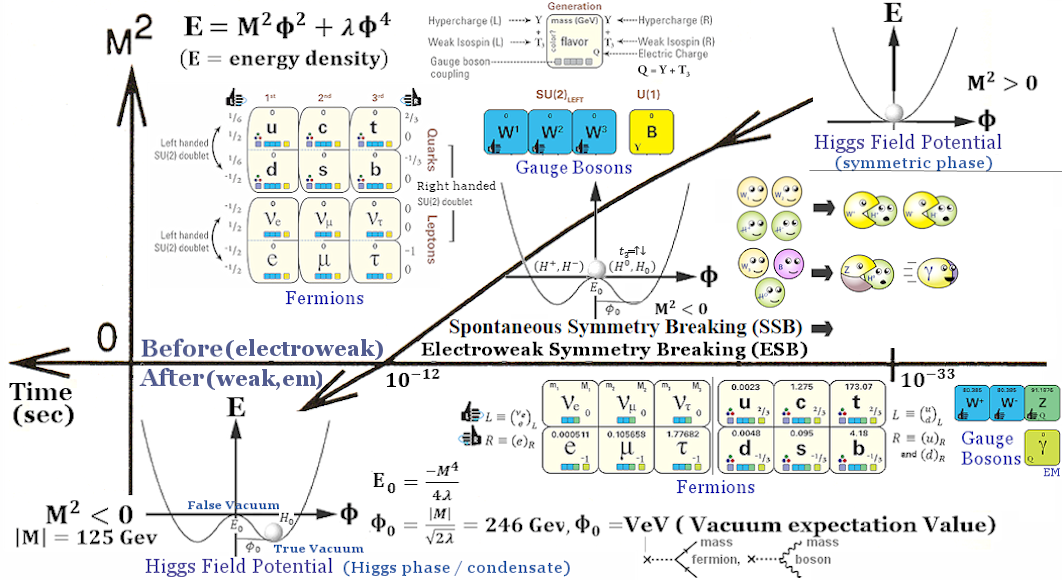 |
transformation of electroweak bosons to (W+, W-, Z) bosons involves the combination (eating as shown in Figue 17) with the three Goldstone bosons from the Higgs to acquire the longitudinal polarization (equivalent to endowing mass). The transformation also breaks the left/right handed symmetry. The left handed one still has SU(2) gauge symmetry running both weak and electromagnetic interactions; while the right handed version is relegated to have U(1) symmetry, (a singlet without neutrino) interacting via electromagnetic only. |
Figure 17 SSB + ESB |
Without further ado, here's the mathematics to show the consequence of SSB using a simplified example of one boson field (see "Spontaneous Symmetry Breaking" for further details of the mathematics) : |

 |
|
Figure 18a SU(3) Gauge Theory [view large image] |
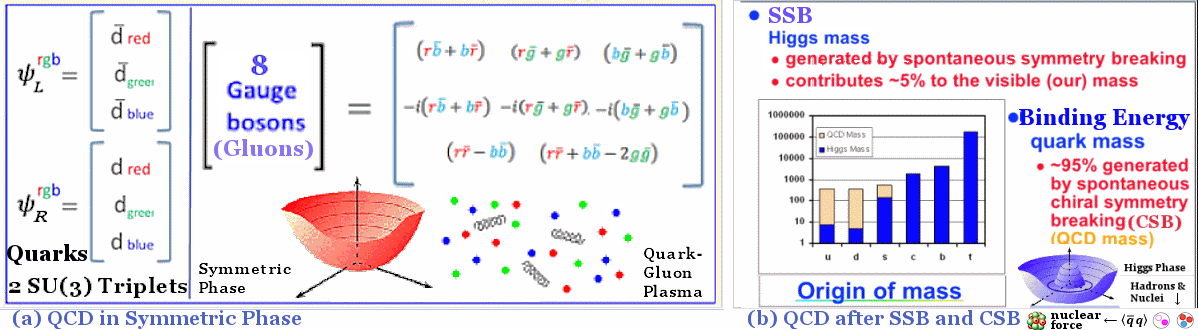 |
|
Figure 18b SSB + CSB |
 0, 0,  +, +,  -) which are the 3 Goldstone bosons from the Higgs with mass contributed by CSB. The pions have minimal mass among all mesons (see "List of Mesons and Meson"). -) which are the 3 Goldstone bosons from the Higgs with mass contributed by CSB. The pions have minimal mass among all mesons (see "List of Mesons and Meson").
|
 B-T plane (for baryon, Figure 19).
B-T plane (for baryon, Figure 19). is a form of potential energy that can be absorbed or released during a chemical reaction or phase transition. It is a function of density, temperature, pressure, ... (see insert in Figure 19 for a simple example). At constant temperature and pressure, the Gibbs free energy G (energy releases to or absorb by the environment) is expressed by :
is a form of potential energy that can be absorbed or released during a chemical reaction or phase transition. It is a function of density, temperature, pressure, ... (see insert in Figure 19 for a simple example). At constant temperature and pressure, the Gibbs free energy G (energy releases to or absorb by the environment) is expressed by :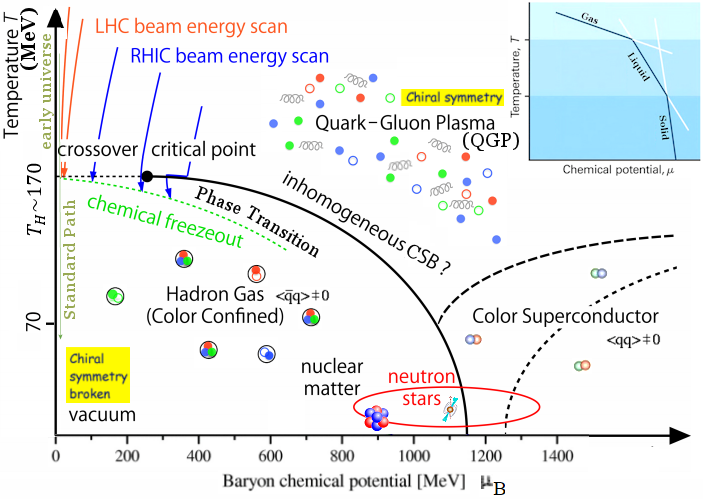 |

|
Figure 19 QGP/Hadron Gas Transition |
 |
The main way of processing crude oil is to separate it using fractional distillation. Oil is made up of many different hydrocarbons of different boiling points (Quantum Fields). The first step in distillation is to boil the oil to a very high temperature (Big Bang), usually around 400oC. When the solution boils, it forms vapors entering the fractional distillation column (GUT), which has many trays to collect the liquid (Quantum Fields). As the height in the column increases, the temperature gets cooler, so as the vapors rise, they cool. Since every hydrocarbon chain has a different boiling point, as a chain reaches a height where the temperature is lower than the boiling point, it will cool into a liquid and be collected by a tray (Symmetry Breaking Processes). This method allows for all parts of the oil to be separated and collected so that they can be further processed and refined (Standard Model). A very good animation of the distillation process can be found in Figure 20. |
Figure 20 Q Fields Evolve and Crude Oil Distillation |
According to this scenario, all the quantum fields were unified (mixed together) in the beginning. Each one emerges from the whole and manifests its characteristics only at suitable temperature by the process of Symmetry Breaking. Ultimately, it is the cosmic expansion (which keeps lowering the temperature) that causes all these cosmic phase changes (Figure 09). |