Many-Body Problem (2022 Edition)

Quantum Mechanics :
   Hartree Fock Method (HF)
   Molecular Orbital
   Density Functional Theory (DFT)
   Diatomic Moleucle
   Band Theory
Plasma Physics (Fluid Dynamics)
Ideal Gas and Real Gas (Thermodynamics)
Newtonian Mechanics :
   Constant Gravity
   Reduced Mass
   Planetary Motion
   Three-Body Problem
   Rigid Body
   Space Flight

In both classical and quantum physics, exact solution in closed form can be obtained only in system involving 1 or at most 2 particles. However, there are infinite number of particles in the real world. Under the title of "Many-Body Problem", various kinds of approximates

	are employed to evaluate the physical properties. The followings use the Many-Body Schrodinger equation to illustrate how it is done to extract information about the many-body systems from individual atom to solid (Figure 01), then expanding to macroscopic systems and gravity.
Figure 01 Many-Body System [view large image]

Hartree Fock Method (HF)

The full glory of Schrodinger equation for many-body system is shown in Figure 02. It is intractable for system of more than 2 particles. An immediate simplification is to separate the system into 2 parts - one for the electrons and the other for the nuclei because electrons moves much faster, its motion is almost independent of the nuclear movement. This is called Born-Oppenheimer Approximation.


Figure 02 Schrodinger Equation, Many-Body [view large image]	See Figure 10 for a pictorial portrait of *U_e(R)*.

The electronic Hamiltonian is simplified further by removing V_NN which is just a constant for the fixed set of nuclear coordinates R_ab. The requirement of antisymmetry (Pauli's Exclusion) principle for the wave function is satified in the form of Slater determinant :

Under these modifications, the electronic energy U_e is replaced by the Hartree Fock energy E_HF (see Eq.(1)) :


Figure 03 Stationary Orbital [view large image]	See "An Introduction to Hartree-Fock Molecular Orbital Theory" for the original derivation, "Stationary-action principle", and "Lagrange multiplier".

[Top]

Molecular Orbital


Figure 04 H₂ Molecular Orbitals [view large image]

See "definition of F(x₁) in Eq.(4a)".

Since the Coulomb integral F_aa is negetive, the ordering in energy levels is correct in Figure 04 for the case of parallel spin.

The above example is applicable to the (H₂)⁺ molecule, one electron of which has been dispatched to infinity. It is similar to the case of atomic hydrogen ion (proton) H⁺ for which all the energy levels have been calculated by solving the Schrodinger equation (with M = 1, N = 1 instead of M = 2, N = 2, see Figure 02) exactly. See "Molecular Orbital Theory" for more H₂ molecular orbitals.

[Top]

Density Functional Theory (DFT)

The Density Functional Theory (DFT) replaces the individual electrons with one electron density greatly simplified the formulation as shown in Figure 05. The theory takes advantage of the fact that it is not necessary to know the wave functions of all N electrons. Knowledge of one or two interacting electrons is sufficient, i.e, one form fits all (each term looks the same as the others). Thus, the electronic Hamiltonian H_e (in Eq.(1), minus V_NN) has this explicit mathematical form :


Figure 05 Density Functional Theory (DFT) [view large image]	There are two problems with this formulation : (1) It fails to incorporate the density n(r₁) into the kinetic energy term T_e. (2) It does not support the exchange energy E_ex (the last term in Eq.(10b).

These problems are addressed variably by trial orbital or fictitious electron density. The "Local Density Approximation (LDA)" is selected as an example here. For evaluating the kinetic energy T_e, the scheme is to place N non-interacting electrons in to a box of volume, V, with a positive background charge keeping the system neutral, i.e., the electron density n = N/V = constant (see Figure 06).


Figure 06 Local Density Approximation	See "Figure 06, and Density of States, Fermi Energy and Energy Bands".


Figure 07 r and k Space of Lattice [view large image]	See "Figure 07, and Solid State Physics" for Reciprocal Lattice.

Returning to the interacting electrons, it is assumed that the density dependence (in exponential power) is similar to the non-interacting case. Thus, according to Eqs. (10,a,b), (14) and (15b), the electron energy can be expressed as the functional of n :
U_e[n] = V_eN[n] + T_e[n] + V_ee[n] ---------- (16a)
Similar to the HF Method, the DFT's ultimate task is to minimize U_e[n] together with the constraint
P = n(r)d³r - N = 0, i.e.,

L[n] = 0 ---------- (16b),
where L[n] = U_e[n] -

P[n] ---------- (16c).

Figure 08 Stationary
Density

See Figure 08.

In addition, there is this so-called Correlation interaction, which is also a result of the Pauli Exchange interaction. In the absence of precise knowledge of its nature, it is often assumed that its energy E_c is the error between the exact ground state energy E₀ and approximate calculation, i.e.,
E_c = E₀ - U_e ---------- (17).

By early 21 century, attempts are made to link the correlation interaction with entanglement. Here's one example to calculate U_e = E_HF with the HF method and thus E_c from Eq.(17). Then uses the same method to compute the single-electron density n(r₁)/N in Eq.(11a). The nomenclature in "entanglement" research uses

(x,x') instead of n(r₁)/N. The single electron coordinate r₁ has split into x and x' to represent 2 opposite spin states and

(x,x') becomes a matrix called "density matrix" (see "von Neumann Entropy").
The von Neumann entropy S(

) is the quantum version of the "Shannon's Measure of Information" :
SMI = - _i p_ilog₂(p_i), i.e.,
S(

) = -Tr[

)] ---------- (18),
where Tr is the trace of the matrix.


Figure 09 Entanglement and E_c [view large image]	Entanglement Measure and E_HF (and thus E_c from E.(17)) has been calculated for 10 Helium-like atoms, e.g., H^-, He, ... Ne⁺⁸ as shown in Figure 09. It shows a definite correlation between the 2 entities (see original article on "Correlation energy as a measure of non locality")

Although entanglement between microscopic particles lasts for very short interval of few seconds or less, it is very important in "quantum computing" (see more in "Entanglement and Teleportation").

[Top]

Diatomic Molecular

As shown in Figure 04,a, the 2 low laying electronic states of H₂ have energy U_e(R), which becomes the potential energy to confine the atomic nuclei (Figure 10,a). There are various theoretical models to provide analytical approximation to the real thing. The simplest one is the Harmonic Oscillator, which is suitable for a range near the minimum of the potential curve (see Figures 10,b, and 11).

The Harmonic Oscillator is one of the basic ingredients of quantum mechanics. Its solutions are in closed form which enables relatively easy visualization. The usefulness is derived from the Taylor expansion of any function including the potential energy curve U_e :

	The second term with the first derivative tends to vanish near the minimum of any function, while the first term is a constant which would not affect the physics. Thus, only the quadruple term survives with the other terms being negligibly small and this is precisely the form for the potential energy of the harmonic oscillator.
Figure 10 Potential Curve [view large image]	Thus, U_e = k(R-R_e)²/2, where k =[d²U_e/dR²]_{R=R_e} ---------- (20).

The Harmonic Oscillator Schrodinger equation
H

_n = (p²/2m + m

²x²/2)

_n = E_n

_n ---------- (21),
where p = -i

d/dx, and

² = k/m. The eigen value (energy level) is E_n = (n + 1/2)

. The zero point energy

/2 usually is subtracted from the formula to avoid infinite energy in the vacuum. The wave functions can be expressed in terms of the Hermite Polynomials H_n(x), i.e.,

_n(x) = C_ne^-x²H_n. The explicit forms for few low lying states are shown in Figure 11. The formulation of quantum harmonic motion is useful in studying the vibrational modes of molecules and crystal lattice.

Figure 11 Quantum SHM Wave Functions [view large image]

The Morse curve U_e = D_e[1 - e^-a(R-R_e)]² ---------- (22)
(see Figure 10,b) is a more realistic model, where D_e is the dissociation energy at R

,
"a" determines the width of the curve, and R_e is derivated from dU_e/dR = 0.

In presenting the potential curve for a diatomic molecule, one of the atomic nuclei is usually fixed at the origin of the coordinate frame. The other nucleus is then portrayed as vibrating and rotating inside the potential well as shown in Figure 10. The vibration is restricted to discrete energy levels. Each of the vibrational energy level v is further split into a series of rotational energy levels J called vibrational band. When the Schrodinger equation of Eq.(21) is expressed in spherical coordinates, separation of the spatial variables and wave functions into Y(R),

(

), and Z() turns it into 3 equations :

Figure 12 Energy Levels
[view large image]

See Figure 12,a for energy levels and "Associated Legendre Polynomials"; while Y_{Jm_J} = P_J^m_J e^im_J is called Spherical Harmonic.

The electric dipole transition is the dominant effect of the interaction between the electrons in a molecule with the electromagnetic field. The transition probability amplitude from an initial state

to a final state

' is in the form :

The integral in Eq.(25) with the overlapping vibrational wave functions

_v is the essence of the "Franck-Condon" principle. In layman's language, it states that the preferred transition occurs when the initial and final wave functions overlap more significantly. This condition is satisfied most often at the turning points, where the momentum is zero as shown by the (blue, green) transition arrows in Figure 10,b).

Transitions are also governed by selection rules, which usually allow transitions to occur only between change of the rotational or vibrational quantum number by an amount of 0 or

1 at a time. Mathematically, it is the transition probability in Eq.(25) that determines whether a transition would occur. Here's a simple example of transition induced by the z-component of

_e, i.e.,

_z =

_e cos(

) :

Similar consideration shows that the selection rule for Harmonic Oscillator is

v =

1. The electronic selection rule should abide to those for rotation, vibration, plus total spin

S = 0. See Figure 12b, "Selection Rules" and "Selection rules and transition moment integral".

[Top]

Band Theory

	About 80% of the free elements at room temperature exists in the form of metal. The conditions to form metal are vacant valence orbitals and low ionization energies. Similar to the splitting of energy levels when two or more atoms come close to each other; (See Figure 04.) energy levels broadened to a band (many closely spaced energy levels) for an aggregate of many atoms as shown in Figure 13,a.
Figure 13 Band Theory [view large image]	See "Solid State Physics".

Due to the "Exclusion Principle" or equivalently the "Fermi-Dirac statistics", the valence electrons from the sodium atoms cannot occupy the same energy level of each others, they fill up the energy bands up to half of the 3s band at 0K (because the 3s level is only half filled, it can accommodate 2 electrons but there's only 1 in sodium atom), at an energy called Fermi energy E_F. Figure 13,b shows that if there is empty levels available in the energy band, the valence electrons will be able to roam among the space in between the atoms by absorbing energy from the environment when the temperature is above 0K. With a few exceptions, metals have a silvery-white color because they reflect all frequencies of light. They have high electrical and thermal conductivity and all metals can be drawn into wires or hammered into sheets without shattering, i.e., they are ductile and malleable. These attributes are

the result of mobile, non-rigid electron gas within the lattice. Most metals (except gold, silver, platinum, and diamond) do not occur as free elements in the Earth's crust. They are usually found in chemical combination with other elements as mineral ores. Figure 13,b also shows that in an insulator, the valence band is full and the next empty energy band is separated by a large energy gap. Conduction cannot occur unless some of the electrons in the valence band are promoted to the conduction band. Energy needed to promote a few electrons might be provided by heating the solid to a very high temperature or by shining X rays on it. No solid can remain a good insulator while it is exposed to X rays. A semi-conductor has a smaller energy gap. Electrons can be promoted to the conduction band as a result of irradiation such as the conversion of sunlight to electricity by means of a silicon cell.

		The formation of band structure as shown in Figure 13,a is based on the model of "Free Electrons". Actually, there are atomic nuclei, which is characterized by periodic separation "a" with a corresponding potential V_G(r) = V_G(r+a). As shown in Figure 13,c and its magnifying version in Figure 14, for most values of the variable k = 2/, the electron energy E⁰ = ²k²/2m_e. Only at k = n/a, the energy splits to E_G = E⁰ V_G(k), where V_G(k) is the Fourier transform of V_G(r). This is the origin of the "Band Gap".
Figure 14 Band Gap [view large image]	Figure 15 Semiconductor Doping [view large image]	However, the band gap can be altered by in-purity doping which has the effect of narrowing the band gap as shown in Figure 15 either by adding electrons or introducing holes in the conduction band. This is the idea of semi-conductor.

[Top]

Plasma Physics

Plasma is the fourth state of matter in which the components of the atom become separated. It is not produced by phase change. Its production depends on the separation of the atomic nuclei and electrons. Once detached, they move around independently and form a globally neutral mixture. Plasma is found in the stars and the interstellar environment making up most of our universe (~ 99 %, = 100% in early universe) under a wide range of temperature and density (Figure 16a). However, such condition does not occur frequently on Earth and that's why life can exists here. In our everyday life, plasmas have many applications (including nuclear-fusion, micro-electronics, television flat screens and so on), of which the commonest is the neon tube.

The Schrodinger equation is useless in describing the dynamics of plasma. The equations of motion are prescribed by the "Navier-Stokes Equations" in fluid dynamics.

Figure 16a Plasma Physica
[view large image]

There is no problem with the Quantum Theory, the failure of the Schrodinger equation in this case only reflects that different platform is used to describe different system by the reductionist's approach. It employs different method/theory for each different level and merge the various levels together at the ends. Usually the connection is to adopt the derived quantities or properties at the lower (smaller size) level

as input parameters or established facts from the theory for the higher (larger size) level. Details in the lower level can be neglected by the theories for higher levels (such methodology is called "Effective Theory"). Figure 16b illustrates some of the systems according to the size of their components. The classification is incomplete as there are many more systems below, above, and in between.

Figure 16b Reductionist's Systems [view large image]

Anyway, here's an example of "Magnetohydrodynamics (MHD) and the Formation of Jet from Black Hole" :

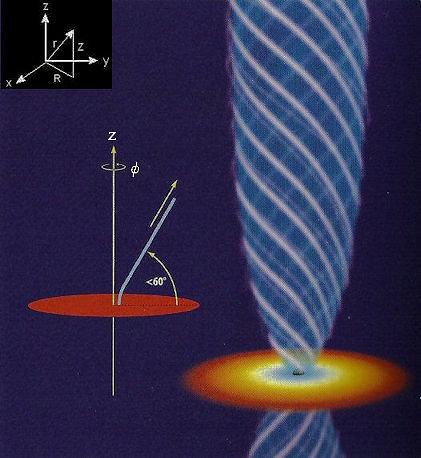Nobody has seen a black hole until the silhouette in M87, 2019. Nevertheless, schematic diagram such as the one shown in figure 16c invariably presents a system composed with a central object (the black hole), an accretion disk, and a pair of jets moving along twisted magnetic field lines. This picture of the black hole is based theoretically on the combination of three branches of physics - Fluid Dynamics, Electromagnetism, and Gravitation.

The effect of gravity from the black hole is characterized by the escape velocity v_esc(r) = (2GM/r)^1/2, where M is the mass of the black hole, and r = (R² + Z²)^1/2 provides a link between the spherical and cylindrical coordinates (see upper left corner insert in Figure 16c).

With the assumptions of infinite conductivity (for the plasma in the system), isotropic pressure, local charge neutrality, non-relativistic inter-particle speeds), the suite of MHD equations are :

Figure 16c Black Hole Schematic [view large image]

These set of equations can be solved only through numerical computation. In general, the magnetic field has only the z component B_z initially. When the accretion disk is set into rotation, the field lines is wrapped around the rotation axis creating the helical field in the z direction. As ionized matter cannot cross field lines, it is obliged to follow the lines and thus form a collimated jet (Figure 23). The following is a scenario of the numerical computation according to a letter in Nature with the title "A magnetic switch that determines the speed of astrophysical jets".

A dense accretion disk (dark disk in Figure 16d) orbits a compact object of mass M.

Acceleration takes place mostly at R₀ ~ 3.6 R_s, where R_s = 2GM/c² is the Schwartzschild radius.

The dense disk is sandwiched by two layers of tenuous corona (shown stippled) whose temperature is hotter than the disk but still colder than that in the halo. The coronal density is assumed to be 10 times the asymptotic halo density, and the disk density is essentially infinite in the simulations.

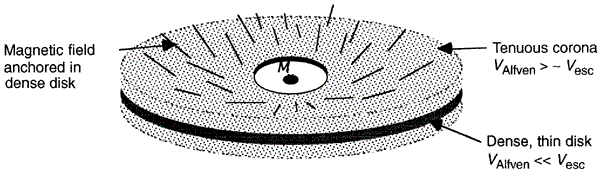Figure 16d MHD Computation
[view large image]

Open magnetic field lines, making an angle

= 30^o with the rotation axis, protrude from the disk and through the corona initially. The lines are dragged along by rotation creating a B component.

The corona is replenished continually from the disk. The coronal flows are decidedly jet-like. The flow speed is a strong function of the ratio

= v_A/v_esc. The jet speed is low for

< 1, i.e., for weak magnetic field (relative to gravity). The speed rises sharply when

> 1. The ratio

is therefore referred to as "magnetic switch" to turn on a pair of jets from a state with no jet.

Figure 16e shows the jet speed as a function of coronal magnetic field strength for both stellar disk (lower and left axes) and black hole's (upper and right axes). The v_c for the proto-star is the velocity at

Figure 16e Jet Switch

r_c = 2x10¹² cm ~ 30 R_sun, while

= (1 - v²/c²)^-1/2 is the Lorentz factor and

= 11(v_A/c)² for the black hole. The two dash lines are taken from the "Relativistic Wind Theory" which excludes the effect of gravity.

proto-stellar object

_esc

_jet

^1/2

Hannes Alfven

^1/2

Plasma Confinement for Nuclear Fusion

Spiral Flow 2 and Density Wave (2022 Edition)

[Top]

Ideal Gas and Real Gas

Thermodynamics is a branch of physcis developed in the 19^th century. It began with the invention of the steam engine (Figure 17) at the beginning of the industrial revolution. It was driven by the need to have a better source and more efficient use of energy than the competitors (among English, French, and German). It was a case where technology drove basic research rather than vice versa. Thermodynamics provides a macroscopic description of matter and energy. Today better insight is obtained by linking the subject with the statistical behavior of microscopic particles. They are gas molecules that can collide and possibly interact with each other. Since it's hard to exactly describe a real gas, it is often substituted by the Ideal gas as an approximation, in which the particles interact only by elastic collision, and take up no volume.

Figure 17 Steam Engine [view large image]

For example, the phase rule indicates that a single component system (c = 1) with only one phase (p = 1), such as liquid water, has 2 degrees of freedom (f = 1 - 1 + 2 = 2). For this case the degrees of freedom correspond to temperature and pressure, indicating that the system can exist in equilibrium for any arbitrary combination of temperature and pressure. However, if we allow the formation of a gas phase (then p = 2), there is only 1 degree of freedom. This means that at a given temperature, water in the gas phase will evaporate or condense until the corresponding equilibrium water vapor pressure is reached. It is no longer possible to arbitrarily fix both the temperature and the pressure, since the system will tend to move toward the equilibrium vapor pressure. For a single component with three phases (p = 3 -- gas, liquid, and solid) there are no degrees of freedom. Such a system is only possible at the temperature and pressure corresponding to the Triple point.

Figure 18 Phase Diagram
[view large image]

One of the main goals of Thermodynamics is to understand these relationships between the various state properties of a system. Equations of state are examples of some of these relationships such as
the ideal gas law:

moles

²³

The Ideal Gas Law

The Concord Consortium

van der Waals force

		In fact, it is these forces that result in the formation of liquids. By taking into accounts the attraction between molecules and their finite size (total volume of the gas is represented by the red square in Figure 19), a more realistic equation for the real gases known as van der Waals equation was derived way back in 1873 :
Figure 19 Ideal Gas Modification	Figure 20 Real Gas [view large image]	(P + an²/V²) (V - nb) = nRT ---------- (29a) where "a" is related to the interaction and "b" for the finite volume (see insert in Figure 19). Figure 20 lists these constants for some real gases.

⁴

₂

Origin of Life

Non-equilibrium Thermodynamics

[Top]

Newtonian Mechanics

	Eq.(30) looks formidable and the graphic is entangled (see Figure 21). However, there is one saving grace : the gravitational force is always attractive concentrating huge mass such as galaxies, stars, ... and the Earth.
Figure 21 Newtonian Many-Body	This disposition reduces the many-body "mumbo jumbo" to one single dominating force center under which everything moves, finer details could be added as perturbation. Here's a few examples to illustrate the usefulness of Newtonian mechanics over the last 400 years (see Figure 22).

	Gravity on Earth's surface (constant external force, 1 body) - The mass M of the Earth creates a constant force mg at its surface, where m is the mass of whatever object at the surface, g = GM/R² = constant in which R is the radius of the Earth, and G = 6.6742x10^-8 cm³/sec²-gm is the gravitational constant.
Figure 22 Applications [view large image]	The Many-Body problem in Eq.(30) is reduced to d²y/dt² = g, the solution of which is y = gt²/2 + vt + h (see Figure 22,a) - the trajectory of a projectile.

Classical Harmonic Oscillator

Reduction of 2-Body to 1-Body Problem (no external force, i.e., F_i = 0) -

Figure 23 Two-Body System
as derived from Eq.(30), and see Figure 23.

Planetary motion (presence of other planets is completely ignored, mass of the Sun is ~ 1000 times more than the planets) -

While the angular momentum L = mvr remains to be a constant for orbital motion in general, the equation of motion in the radial direction becomes more complicated since the centripetal and centrifugal forces do not balance as shown below.


Figure 24 Kepler's Three Law [view large image]	This is the Kepler's 1st Law. The 2nd Law is expressed by dA/dt = L/2m = constant, where dA = (r²/2)d. While the 3rd Law is covered by T = ab/(dA/dt) giving T² = (4²/GM)a³ (See Figures 24, and 22,b).

Three-Body Problem -

At the end of the 19th century, the French mathematician Henri Poincare tried to solve the differential equations for the three body problem. It was noticed that the orbit is not periodical anymore (in contrary to the case with just two bodies), actually the motion appears to be random. Then it was found that the solution is "exquisite sensitivity to initial conditions". The object would follow a very different path at the slightest change of initial condition. Figure 25 is an animation showing two paths of a third body under the gravitational influence of two massive objects. The paths start at the same position but the velocities differ by 1%. Initially the paths are very close, the difference becomes apparent after a while.

Figure 25 3-Body System

Although there is no solution for three-body problem in closed form, it turns out that there are points in a three body configuration with two large and a much smaller ones on which the forces are balanced. They can rotate together as a whole. The five such locations are called Lagrangian points L1, ... L5. Following is the mathematics to derive the location of the smaller object r at L1 with respect to M₂; R is the distance between M₁ and M₂ (see Figure 26). According to a theorem in two-body problem, the two body motion can be reduced to a one body equivalence with center of mass M = M₁ + M₂ and distance R_m = M₁R/M (with origin at M₂). Assuming circular motion, the equation for the balance of contripetal and contrifugal forces can be written as :


Figure 26 Lagrangian Points [view large image]	This is exactly the distance to L1 - the parking lot for many of the artificial satellites. However, it is known to be unstable, thruster burns manoeuvre is required to keep the object in place.

The equation for L2 is similar with (R-r) replaced by (R+r) and changing sign for the 2nd and 4th terms. The approximate distance r is the same as the one for L1. BTW, see "Cubic Formula" for cubic root calculation. The approximate formula for r is obtained by neglecting the r⁵, r⁴ powers and taking only the leading term in the cubic formula.

The parking spot for the James Webb Space Telescope (JWST) is at L2 shielding it from the light and heat of the Sun.

See "Synchronous Rotation" for another application of Newtonian mechanics to celestial bodies.

Rigid Body - Since the Newtonian's equations of motion cannot be solved in closed form for three particles and beyond, it seems that the case for many particles would be much worse. However, such system can be described with mathematical precision if the separation between the particles is constant, that is, it is a rigid body, which is a good approximation to many solid objects. It will be shown below that the dynamics can be reduced to two equations - one for the translational motion of the center of mass, and the other for the rotation around the center of mass (an additional vibrational mode has to be considered for microscopic oscillation of the individual constituents, see specific heat). As shown in Figure 27a, if the reference point for the particles in the solid is shifted to the center of mass such that

_i m_ir'_i = 0, r'_i = constant, then the equations of motion can be written down in terms of the force F and torque T summing over all the particles in the system :


Figure 27a Rigid Body System	Figure 27b Moment of Inertia	The rotational term can be neglected if the size of the solid is much smaller than the distance scale. The object becomes a point mass without structure, either because it is so "small" or it can be represented by the Center of Mass.

That's why a galaxy of size ~ 10²² cm can be treated as a point in context of the cosmos at the scale of ~ 10²⁸ cm. Another example is the planets with size no bigger than 10¹⁰ cm in orbit of about 10¹³ cm or further from the Sun. Actually, these examples are just one of the reductionist's views of the world, which maintains that details of lower levels can be neglacted in higher level (see "Effective Theories").

Space Flight - The spacecrafts spend most of their flight time moving under the gravitational influence of a single body � the Sun. Only for brief periods, compared with the total mission duration, is its path shaped by the gravitational field of the departure or arrival planet. Thus, the mission can be categorized into 3 phases as described below (see Figure 28). Each one is under the influence of a dominant mass with perhaps small perturbations in between.

Launch (Earth Domain) - First of all, the spacecraft has to attain the escape velocity v_esp = (2GM/R)^1/2 to overcome the attractive force of the Earth (where M is the mass, R the radius of the Earth). At a distance of about 10⁶ km from

		Earth when the spacecraft reaches hyperbolic excess velocity v = (GM/\|a\|)^1/2 (see Figure 28a - the hyperbolic curve), the flight can be switched to the heliocentric frame of reference (for both the velocity of the spacecraft relative to the Sun and the subsequent heliocentric orbit, see Figure 28b). The total orbital energy E for mass m near the Earth is : E = mv²/2 - mGM/r = mGM/(2\|a\|) = constant > 0 ---------- (31).
Figure 28a Conic Curves	Figure 28b Reference Frames [view large image]	It is bound to the Earth for E < 0, free-run for E > 0, and just enough to escape for E = 0. See "specific orbital energy" = E/m = GM/(2\|a\|) = constant.

		In Flight (Sun Domain) - At some point during the lifetime of most space vehicles or satellites, their orbital elements (see Figure 29a) have to be altered. For examples, it is necessary to transfer from an initial to the final orbit (see Figures 29b, 30,b and "gravity assist"), rendezvous with or intercept another spacecraft, or correct the orbital elements for perturbations. To change the orbit of a space vehicle, we have to change its velocity vector in magnitude or direction. Most propulsion systems operate for only a short time compared to the orbital period, thus we can
Figure 29a Orbital Elements	Figure 29b Orbital Transfer	treat the maneuver as an impulsive change in velocity while the position remains fixed. See "Cassini's Flight Path".

	Descent (Planet Domain) - As the spacecraft arrives at its destination, it has to decelerate and transfer to the local frame of reference. As shown in Figure 30,c it may need a heat shield to protect its reentry and firing retro-rocket to touch-down slowly depending on the kind of mission.
Figure 30 Space Flight [view large image]	Figure 30,c is an example for landing on Mars (see detail). See a detailed guide on "Rocket and Space Technology", and a course lecture on "Celestial Mechanics".

	By early 21st century, technology has advanced to the point which enables the return of Mars sample to Earth. In April 2018, a letter of intent was signed by NASA and ESA that may provide a basis for a Mars sample-return mission. In July 2019, a mission architecture was proposed to return samples to Earth by 2031.
Figure 31 MSR Concept [view large image]	See "Summary of MSR (Mars Sample Return)"

The Peril


Figure 23 Two-Body System	as derived from Eq.(30), and see Figure 23.