Twistor Theory

Spinors and Spin Network
Twistor and Twistor Space
Connection to Quantum Theory
Twistor Gravity
Further Development

Spinors and Spin Network

Twistor theory has been developed by Roger Penrose and his associates since the 1960s. He realized that using the space-time continuum picture to describe physical processes is inadequate not only at the Planck scale of 10^-33 cm but also at the much larger scales of elementary particles, or perhaps atoms, where the quantum effects become important. He believes that space-time is created out of quantum processes themselves at the subatomic level. The mathematical tool in field theories is not suitable for the new formulation since the field equations are based on well-behaved functions varying smoothly in space-time. Thus his mathematical tool is geometry instead of differential equations. However, space-time descriptions of the normal kind have been used at the atomic or particle level for long time with extraordinary accuracy. Thus, this new geometrical picture must, at that level, be mathematically equivalent to the normal space-time picture - in the sense that some kind of mathematical transformation must exist between the two pictures.

The initial attempt to formulate discrete space-time used spinor as the building block. The spinor is a mathematical object that is used in the quantum theory to describe the spin of the elementary particles. It is the simplest quantum object having only two possible states - spin up or spin down. It is argued that if the distinction between a spin up and a spin down is to have meaning within a quantum theory set in empty space, it seems to imply the spinors actually create their own spaces - a sort of quantum version of the more familiar space-time. Each spinor would therefore have associated with it a sort of primitive space. The rules for putting spinors together involve pure addition and subtraction and have nothing to do with the ideas of continuity. They join together to form a spin network (Figure 01). Each line represents an unit area (

angular momentum), together with an integer on the edge. The integer n comes from the value that the angular momentum of a particle is allowed to have in quantum theory, which are equal to n

/2. The dot represents the unit of volume enclosed by the areas according to the number of

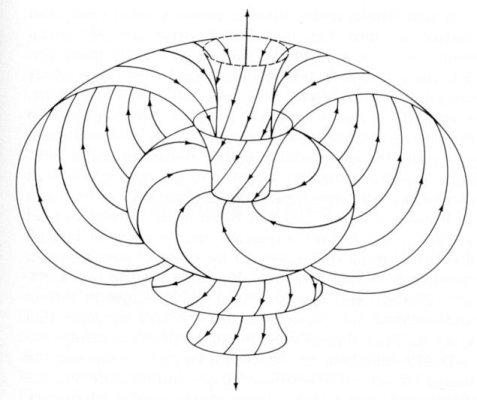
connecting lines. Two spin networks would not join smoothly similar to the impossibility of covering a curved space by a patchwork of small, flat spaces. This is taken to mean that the overall space is curved, or to put it another way, the very fact of this failure to join is the curvature of space. In the limit, when the number of spinors becomes infinite; a continuous picture of space arise. Even though this is a provocative concept, but in the end it is not useful for the unification of quantum theory with geometry. The space created is incomplete, it is static and nonrelativistic, and it contains no sense of distance or of separation. However, the idea of spin network has now become a key concept in loop quantum theory.

Figure 01 Spin Network
[view large image]

[Top]

Twistor and Twistor Space

It was believed that the new quantum object must combine angular momentum (spin) with linear momentum, and on an equal footing. It must be an object that is both spinning and moving along. In addition, it must be both quantum mechanical and relativistic. Penrose's twistor was to fulfill all these requirements. It was also to bring together a number of other key ideas: the significance of complex numbers and their geometry; the role played by light rays (null lines) in relativity, and the special ways in which physical solutions are singled out in quantum field theory (the solution with positive frequency).

The twistor space is defined by four complex dimensions. Since a complex number consists of two independent parts (such as Z = X + iY), it should contain more information than the "conventional space-time" (henceforth abbreviated to "space-time") with four real dimensions. A twistor Z is a point in this twistor space. Multiplication of Z by its complex conjugate Z* defines the helicity or degree of twist (of the twistor) s = (Z Z*) / 2, which is a real number. All the twistors with zero helicity s = 0, lie in a special region of twistor space which is labeled as PN in Figure 02. It divides the twistor space into two regions, PT⁺ and PT^- (Figure 02) corresponding to twistor sub-space with positive or negative helicity. This division is the geometrical analogue of the way in which solutions in quantum theory are divided into positive and negative frequency parts.

		Points in PN represent twistors with zero twist, and it turns out that they correspond to light rays or null lines in space-time. In Figure 02, while the points A, B, and C in twistor space correspond to lines in space-time, the line P in twistor space corresponds to a point P in space-time - the intersection of the lines A and B. This means that a point in space-time is nonlocal in its deeper nature. The origin of space-time now appears very different when viewed from the
Figure 02 Twistor Space and Space-time [view large image]	Figure 03 Congruence of Null Lines [view large image]	twistor perspective. A twistor in the PT⁺ or PT^- region has to be represented in the space-time picture by a collection, called a congruence, of null lines that twist around each other in a right-handed or left-handed sense (see Figure 03).

As things have worked out so far, twistor theory has not moved much in the "combinatorial" direction of spin-networks. Instead, the (seemingly) very different complex-analytic aspects of twistors have been the ones that have proved to have greatest importance. The one place where the possibility of a connection with spin-network theory remains fairly strong is in twistor diagram (interaction between twistor spaces in term of a graph similar to the Feynman diagram).

[Top]

Connection to Quantum Theory

The fact that space-time points are derived from twistor intersections (see Figure 02), implies that they would not survive when quantum processes are introduced into the twistor picture. In effect, certain transformations or processes in twistor space turn out to be equivalent to quantum processes in space-time. It is found that a quantum transformation in twistor space mixes up the twistors (more detail in the following paragraphs). But since points in space-time are defined in terms of conjunctions of lines in twistor space, this means that the space-time point will smear out. Thus, at the quantum level, the twistor space picture suggests that points in space-time lose their distinction and become fuzzy - similar to the uncertainty of the position of an electron in quantum theory, but now it is the very structure in the scaffold being not well-defined.

As mentioned earlier, a point in twistor space corresponds to a complex twisting structure of null lines in space-time (Figure 03). In the special case when the point lies in the PN region, it corresponds to a single null line. A consequence of this space-time structure in null lines is that it is now conformally invariant because it is not possible to transform a line of zero length into a finite length. Thus, it is totally indifferent to the scaling of length. Since only massless particle can move along the null line, it seems that this structure of space-time cannot accommondate particles with mass. It is suggested that interaction with gravity would break the conformal invariance and endow mass to the particles. Exactly how such mechanism works in terms of the geometry of the corresponding twistor space has become a major research topic for Penrose's group.

It is found that when curvature such as gravitational wave is introduced into the space-time picture, it produces transformations of the points in twistor space. Specifically, it mixes up twistors and their complex conjugates - a twistor and its complex conjugate become interchanged. This looks suspiciously like what happens during a quantum process - the twistors themselves behave in similar ways to quantum operators such that the ordered operation Z*Z produce an outcome different from ZZ*. Therefore, the passage of a gravitational wave looks like an actual quantum process in twistor space. Figure 04 shows the symmetry between quantum process in twistor space and gravitational wave in space-time. In Figure 05, a plane-fronted

		gravitational wave passes through a previously flat space-time. Each of these two flat space-times now appears warped when viewed from the perspective of the other, and it becomes impossible to join them in a totally smooth way. The null line Z in one half of the space becomes the null line Z* in the other. The corresponding picture in twistor space is for the twistor to become "mixed up".
Figure 04 Quantum Process [view large image]	Figure 05 Warped Space in Space-time [view large image]

Interaction of massless fields can be described by a twistor diagram in twistor space (see Figure 06). It is similar to the trouser diagrams in string theory, where it gives a pictorial representation of how two free loops meet, interact, and emerge again as free loops. The complexity of the interaction corresponds to the number of holes within the trousers. In the corresponding twistor picture, the free states are represented by the PN region of twistor space. The interacting region is created by stitching copies of twistor space together. Finally the free PN regions emerge again.

Figure 06 Twistor Diagram [view large image]

[Top]

Twistor Gravity

Since Penrose's approach is based on the proposition that mass is a secondary quality that arises in the interaction of more fundamental massless objects, the description of field in twistor space starts with the twistor formulation for massless fields such as those for the neutrino, photon, and graviton. It is found that in place of the differential field equations, Penrose has substituted a simple function in twistor space. The power of twistor mathematics is sufficient to define the field for all time and at all points in space. The whole power of the twistor program is contained within the complex analycity of the twistor functions called "contour integral".

It turns out that any massless field is defined by a contour integral in twistor space. These contour integrals are determined by the poles in a general twistor function in twistor space. It is then possible to re-create the field in its corresponding space-time picture. In space-time the massless particles are specified by their helicity (+ or - helicity denotes parallel and anti-parallel of the directions of spin and motion), they are now labelled by homogeneity in twistor space. The homogeneity of a function could be thought of as a count of the number of powers it contains. For example, a function with terms like 1/x³, 1/x²y, 1/xy², ... has a homogeneity of -3. Table 01 shows the helicity and homogeneity for the massless particles. It shows that at the most fundamental, the twistor picture is not symmetrical.

Particle	Helicity	Homogeneity
Graviton	+2	-6
Photon	+1	-4
Anti-neutrino	+1/2	-3
Unknown	0	-2
Neutrino	-1/2	-1
Photon	-1	0
Graviton	-2	+2

Table 01 Helicity and Homogeneity of Massless Particles

The procedure of defining twistor function was originally applied to the case of photon. It turns out that within the twistor picture, a single graviton requires a very different treatment than that for a single photon. Since a graviton is not only the quantum particle of the gravitational field, it is also a quantum element of the curvature of space-time itself, admitting a single graviton into the twistor picture actually changes its geometry. The very power of twistor space to describe gravity is disturbed by the existence of what it had set out to define. With the introduction of graviton, the structure of twistor space becomes dislocated. Straight lines will no longer join in twistor space once its global structure has become deformed. It is found that the straight lines can be replaced by very general curves that have definite structures. These are called holomorphic curves, which enable the basic contour integral approach to proceed. Translating to space-time, the local things like space-time points are no longer well defined, however, global structures such as null lines and light rays still have their meaning. In addition, the metric of space is a proper solution to Einstein's field equations.

Thus the twistor picture is very different from that for the superstring. For Penrose, gravity and quantum theory must transform each other. While the superstring approach is essentially based upon the assumption that quantum theory remains unchanged right down to immensely short distances and even when the background space was indissolubly linked to the strings themselves.

Table 02 below summarizes the properties of twistor and compares them to the superstring.

Property	Superstring Theory	Twistor Theory
Mass	Massless or > 10¹⁹ Gev	Massless
Length	One-dimensional length ~ 10^-33 cm	Null line
Massless State	Helicity	Homogeneity
Graviton	Spin 2 closed loop	Contour integral with holomorphic curve
Dimensions	Ten real dimensions	Four complex dimensions
4-d Space-time reduction	By compactification	By mapping
Internal Symmetries	Broken by compactification	Broken by gravity
Chirality	Chiral and non-chiral	Basically chiral
Universe's Initial State	Total symmetry	Basic chirality
Formulation	Based on conventional quantum field	Based on geometry
Interaction	Trouser diagram	Twistor diagram

Table 02 Comparison between Superstring and Twistor

[Top]

Further Development

General direction - Very roughly, attempts to implement the twistor program have since 1970 branched into two directions. One is concerned with reformulating General Relativity, i.e. gravity, in terms of twistor geometry. The other is about the twistor reformulation of Quantum Field Theory, i.e. the flat-space theory of elementary particles and forces.
Particles and interactions - The study of twistor algebra is related to the question of whether the properties of elementary particles � their masses, spins and other attributes � can be understood within twistor geometry. Another line of investigation concentrates on the scattering amplitudes for elementary particles, and is largely a question of twistor integral calculus. The calculus requirement turns out to be that of many-dimensional contour integrals of a very special form. They are very conveniently represented by a diagrammatic formalism, which is developed by Roger Penrose in 1970. Like Feynman diagrams, they are based on the idea of getting the amplitude for a physical process by expanding in increasing powers of the coupling constants. Whilst Feynman diagrams evaluate scattering amplitudes as the result of multiple integrations over space-time, twistor diagrams involve multiple integrals in twistor space. However, Feynman diagrams have the essential property of being derived from a general principle (the Lagrangian). Their main problems arise from the fact that they sometimes yield infinite amplitudes. In contrast, twistor diagrams are defined in such a way as to be manifestly finite. They are always compact contour integrals. Many particular twistor diagrams are now known to correspond to particular scattering processes. A general principle from which these examples can all be derived has not been uncovered. But new developments promise a much more realistic goal.
Massive fields - So far only massless fields have been considered in the twistor theory. The next step in the twistor program would be to generalize the contour integral approach to massive fields and in this way attempt to generate the known elementary particles as quantum excitations of these fields. This is a difficult and complicated problem yet to be worked out.
Gauge particle - Another extension is to describe the gauge fields that are used to explain the forces between the elementary particles. It is suggested that an extra geometrical structure called fiber bundle is added to each point in the twistor space. This bundle would be used to append additional information. Then mixing of the twistors would correspond to the gauge field transformations in space-time.
General Relativity - So far twistor gravity is illustrated by only one graviton. When very many quantum gravitons are admitted into the twistor picture, it should be able to show that a curved space-time can be generated by the action of many gravitons in coherent states. In other word, Einstein's classical description of a space-time curved by the action of matter and energy should be recovered via the action of these gravitons.
A new beginning - All these works went rather slowly for forty years, plagued by mathematical difficulties, and seemed rather far away from mainstream developments in physics. But in 2003 the leading theoretical physicist Edward Witten came up with an astonishing new paper, which related string theory with twistor geometry. In January 2005 Witten showed that strings may not need all those extra dimensions after all. It sparked a whole slew of papers from his fellow theorists and interest is still growing. Witten is not quite convinced yet. "I think twistor string theory is something that only partly works," he says. But these events have infused new life into researches on merging the ideas from these two theories. It turns out that the twistor-string theory may be able to simplify the computation of scattering amplitudes from the Feynman diagrams. But so far the discovery offers only a partial description of the possible processes at the LHC.

Twistor Theory

Contents

Spinors and Spin Network

Figure 01 Spin Network [view large image]

[Top]

Twistor and Twistor Space

Figure 02 Twistor Space and Space-time [view large image]

Figure 03 Congruence of Null Lines [view large image]

[Top]

Connection to Quantum Theory

Figure 04 Quantum Process [view large image]

Figure 05 Warped Space in Space-time [view large image]

Figure 06 Twistor Diagram [view large image]

[Top]

Twistor Gravity

Table 01 Helicity and Homogeneity of Massless Particles

Table 02 Comparison between Superstring and Twistor

[Top]

Further Development

Figure 01 Spin Network
[view large image]

Figure 03 Congruence of Null Lines
[view large image]

Figure 05 Warped Space in Space-time
[view large image]