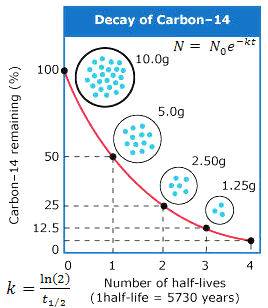

N = N0e-kt ---------- (1)
where k = ln(2)/t1/2, and t is the time variable (Figure 01). Further details are provided in the followings :
| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |
 |
Before the advent of carbon 14 dating, estimate of age is a rather hazardous undertaking. The age of a piece of antique can be determined by its style in certain period, the age of fossil is related to the stratification etc. Discovery of radioactive elements provides the mean to date objects in term of years. The radioactive isotope carbon-14 is especially suitable for dating organic matter because the initial quantity N0 and its half-life t1/2 are known in the decay formula : N = N0e-kt ---------- (1) where k = ln(2)/t1/2, and t is the time variable (Figure 01). Further details are provided in the followings : |
Figure 01 Radioactive Decay [view large image] |
Figure 02 Carbon-14 Dating [view large image] |
 10-12.
10-12. |
|
Figure 03 Mass Spectrometer [view large image] |
the ratio r with the Accelerator Mass Spectrograph (AMS) as shown in Figure 3. |
 |
 |
|
Figure 04 Date Calibration |
Figure 05 Sample Mass [view large image] |
 |
 |
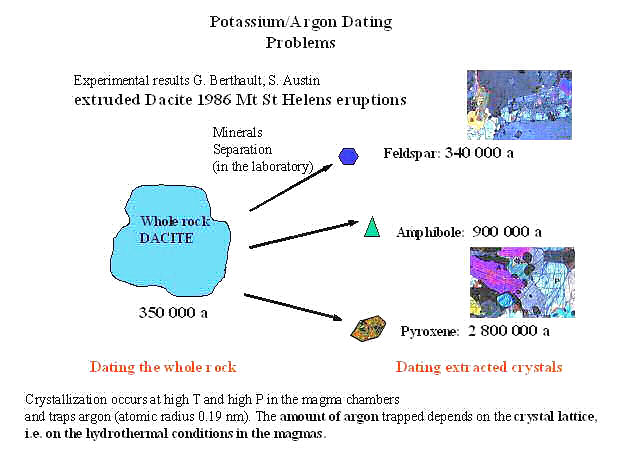
t = (1/k)ln(1+D/P) ---------- (2) where D and P denote the daughter and parent numbers respectively. Since the daughter product argon-40 is not incorporated into minerals, all such atoms in a rock must have come from the decay of K-40 that was there originally. That is, the age can be measured from the ratio D/P using AMS. However, this assumption may not be valid as shown in Figure 06. The measurements obtain three different ages depending on the hydrothermal condition in the magma (from the 1986 |
Figure 06 K-40 Dating |
Figure 07 K-40 Decay |
Mt. St. Helen eruptions). It demonstrates that excessive argon (radiogenic and/or primeval) can yield erroneous ages - a problem readily exploited by creationists. |
 |
For cases where the initial quantity of the radioactive isotope is not available, the method of isochron (equal time) can also bypass the problem with the ratios of parent and daughter to the non-radiogenic isotope of the daughter element as illustrated in Figure 08. The formula corresponds to the plot is in the form : (D + d)/S = (D/P)(P/S) + d/S ---------- (4) where P is the number of the parent atoms, D for the daughter, S (assumed to be constant) is the |
Figure 08 Isochron Dating [view large image] |
non-radiogenic isotope of D, and d is the initial number of D. The formula in Figure 08 is for the case where the horizontal axis is displaced upward by an amount d corresponding to equate d = 0 in Eq.(4). |
 |
Table 01 Radiometric Systems and Dating Ranges |
 |
Optical (Luminescence) Dating utilizes a principle opposite to the radioactive method. Whereas the latter measures the diminished amount of the decaying material, optical dating relies on the accumulation of electrons trapped inside minerals such as quartz and feldspar (the major composition of sediment). The electrons come from the background radioactive elements in the solid, they are trapped in the crystal lattice in the absence of Sun light, which would set the dating clock back to zero by evicting the electrons from the sites. The amount of such electrons measured in the laboratory from a sample is proportional to its age since the last exposure to Sun light. Followings is a summary of such age determination procedure (Figure 09). |
Figure 09 Optical Dating |
 |
Rehydroxylation (RHX) Dating also utilizes the concept of the regular accumulation of something inside the material to determine its age. In this case, it is observed that the mass of fired-clay ceramics, brick, tile etc. is reduced by heating. The subsequent re-absorption of moisture from the environment produces water mass gain, which is found to follow a power law of the time after the initial heating. This dating method is still under development following its introduction in early 21st century. It has been shown to reproduce accurate dates comparing to the known ages of antique artefacts, ancient ruins, etc. Following is a brief description of this method. |
Figure 10 Rehydoxylation Dating [view large image] |
 H2O + O2-. Exposure of the material afterward to water as either vapor or liquid produces mass gain by re-absorption.
H2O + O2-. Exposure of the material afterward to water as either vapor or liquid produces mass gain by re-absorption. (T) t1/4
(T) t1/4 is the kinetic constant depending on the temperature T and type of material.
is the kinetic constant depending on the temperature T and type of material. |
|
Figure 11 Two Types of Diffusion |
 |
Figure 12 Dating the Earth |