Fluid Dynamics and the Navier-Stokes Equations

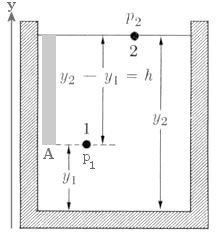
Hydrostatics

		The term "hydrostatics" is applied to the study of fluids at rest, including both liquids and gases. For this special case, u = 0 in the Navier-Stokes equations, the external force F = -g (in the negative y direction) and the pressure gradient is just dp. Eq.(2) is reduced to the simple form: dp = - g dy ---------- (24). Taking point 1 and 2 as shown in Figure 18, integration of Eq.(24) yields: p₂ - p₁ = - g (y₂ - y₁) ---------- (25)
Figure 18 Hydrostatics [view normal image]	Figure 19 Pressure, Atmospheric	which shows that the pressure is less in higher elevation as it is well known in the Earth's atmosphere (Figure 19).

Archimedes' principle states that a body immersed in a fluid is buoyed up by a force equal to the weight of the displaced fluid. Independent of shape and composition, objects of equal volume experience equal buoyant forces. Just for illustration purpose, let us consider a rectangular block of water with height h and area A (perpendicular to page) on the top and bottom faces (the grey stripe in Figure 18). The pressure on the sides will cancel out leaving only a net force to balance exactly the weight of the water block. Mathematically, since the pressure p = f / A, where f is the force exerted on A, Eq.(25) can be rewritten as:

F = f₁ - f₂ = Vg ---------- (26)

where V = h A is the volume of the water block, and F is the buoyant force.

An object will float or sink in the water depending on whether its weight Mg = Vg is smaller or greater than the buoyant force.

Submarine controls the submerging and surfacing by admitting water into a tank or pumping it out. When the submarine is on the surface its ballast tanks are full of air (Figure 20a). The air inside the hull brings the average density of the entire ship below the density of saltwater. Because the sub is less dense, it floats. The average density of a submerging submarine is increased by flooding the ballast tanks with water through flood ports on the bottom of the tanks with the release of air out of the top of the tanks (Figure 20a). Once the overall density of the submarine is equal to the water around it, it has the neutral buoyancy and will remain at that depth. High pressure air is blown into the ballast tanks to push the water out when the submarine is prepared to surface again.

Figure 20a Submarine
[view large image]

Air does not provide a lot of buoyant force because its density is about 1000 times lower. Only balloon filled with low density gas such as hydrogen or helium can rise up to the sky.

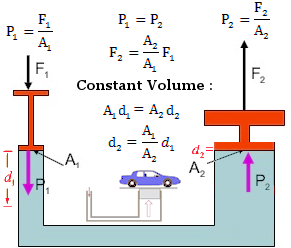
		The principle of hydraulic press operation follows the same rule prescribed by Eq.(25) with g (y₂ - y₁) << p₁, p₂ so that p₁ p₂ as illustrated in Figure (20b), which shows that a smaller force F₁ applied to a piston of smaller cross section A₁ can exert a large force F₂ of proportionally larger A₂. The ideal mechanical advantage is A₂/A₁. Barber chaits, dentist chaits, car lifts, and hydraulic brakes are all devices that make use of this principle. Since volume is constant for incompressible fluid, i.e., A₁d₁ = A₂d₂, thus, the column height d₂ = (A₁/A₂)d₁ is smaller on the lifting side than d₁ on the pressing side.
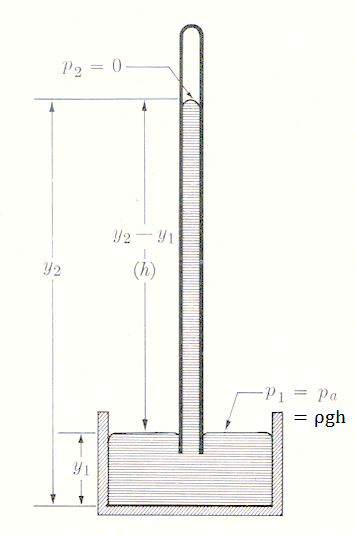
Figure 20b Hydraulic Press [view large image]	Figure 20c Barometer	Another application of Eq.(25) is to make barometer for which p₂ 0 at the closed end of the tube while p₁ = gh is now equal to the atmospheric pressure p_a , which is proportional to the column height h since and g are constants (Figure 20c).