Quantum Field Theory

A footnote on Least Action Principle and Path Integral

This footnote is supposed to clarify the hand-waving argument in the main text with the help of simple mathematics and graphic. The first task is to show that there is a minimum for the action S (for a given Lagrangian L as shown in Eq.(49)) as the paths varies between two fit points. The trajectory of the particle is calculated from the equation derived from the "principle of least action" as shown in Eq.(50).

---------- (49)

Figure 11 Paths
[view large image]

Figure 12 Actions
[view large image]

---------- (50)

The Lagrangian in the sample computation is taken to be the one for harmonic motion in the form :

L = (m/2)(dq/dt)² - (k/2)q² ---------- (51a)

This is the difference between the kinetic and potential energies, i.e., L = T - V, not the total energy E = T + V. It is therefore not a constant or conserved quantity of the motion.

The path in the action of Eq.(49) should be considered as a variable just like the independent variable in a function. It does not represent the actual trajectory of the particle except in some special cases. The equation of motion for the real path is derived from Eqs.(50,51a). To avoid confusion, the actual trajectory is labeled as x instead of q, the result in Eq.(51b) below is just the Newtonian equation of motion with the Hooke`s force law :

m[d(dx/dt)/dt] = -kx ---------- (51b)

The solution of this differential equation is the sine or cosine function or the linear combination of both, e.g.,

x = A cos[(k/m)^1/2t] ---------- (51c)

which is very different from the path specified in Eq.(52a) below. For demonstration purpose, the family of parabolic curves :

q = bt - (a/2)t² ---------- (52a)
dq/dt = b - at ---------- (52b)

will be used to generate the paths between the two end points (0,0), (X,T) as illustrated in Figure 11. If the parameter "a" is taken to be the running index for the different curves, then the other parameter "b" is determined by the end point (X,T) :

b = [X + (a/2)T²]/T ---------- (53)

Each curve in Figure 11 is generated by a Basic program in a home computer with incremental step dt = 0.001 sec :

dq = bdt - atdt ---------- (54)

The action S is calculated by integrating L(q,dq/dt) from (0,0), to (1,4/

) with m = 1 gm and substituting q, dq/dt from Eqs.(52a,b) (see also Figure 01a). The paths in Figure 11 and the corresponding actions in Figure 12 are computed by varying the parameter "a" from -50 to +50 in step of 10. The path traces out a straight line for a = 0. For particle in free space, i.e., for k = 0, the correspondence of shortest path (a straight line) and least action (when S is at its minimum) is exact. The correspondence is off when interaction is taken into account (for example with k = 1 gm/sec², a=(kX/2)/[m-(kT²/10)]

0.6 cm/sec² when S is at its minimum) as if the force field creates a curve space for which the shortest path is not a straight line anymore. Actually, each paths is similar to a numeral devoid of any physical content by itself. They are one step away from the trajectory of a real particle contrary to what some physicists have it interpreted otherwise. Feynman's expression of "sum over paths" in his original work has been altered to "sum over histories" attaching additional meaning as if the paths are real. Furthermore the Lagrangian involved may or may not describe the actual motion of the particle. Additional constraints have to be imposed by demanding invariance under certain operations and it will ultimately be justified by observations.

The link between least action and shortest path has its root back to the 17^th century when physicists in that era discovered that light ray and particles in free space invariably travel in a shortest path between two end points. The "action" is a generalization of the idea to include cases with interaction(s). Thus, to trace backward from the Lagrangian in Eq.(51a) with no interaction, i.e., with k = 0, the action S is reduced to :
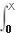S = (mv/2)dq = (mv/2) X = constant

(shortest path) = constant

(actual trajectory) = least action
where the velocity v=dq/dt is a constant in free space. For cases with interaction, the principle of least action is now used to secure the equation of motion instead of shortest path.

		Then along came quantum mechanics and the method of path integral to calculate the transition amplitude between two points, e.g., from t_a = 0 to t_b = T : The sum is supposed to include all kinds of paths imaginable. However, for demonstration purpose the family of paths considered in the previous section is
Figure 13 Path Integral, Real [view large image]	Figure 14 Path Integral, Img [view large image]	sufficient (see Figure 11). The Planck's constant can also be absorbed into the action S so that the computational procedure can be carried over to evaluate the sum.

The result is presented in Figure 13 and 14 for the real and imaginary parts respectively. The blue curve shows the variation of S as a function of "a", while the red curve (not in scale) is the accumulated sum of <0|X> starting from a = -50. The insert displays a much wider range for <0|X> from a = -400 to a = +400. These diagrams demonstrate that the main contribution to <0|X> comes mainly from paths near the classical path (around the minimum of S). The exponential of the action assumes a pattern of rapid oscillation as its value getting larger, the amplitudes tend to cancel out each other leaving a steady value for <0|X> at the asymptotic limit.

An alternate way to perform the path integral is to sum over all the paths at different time t and then put them all together as shown in Figure 15, where the time coordinate is divided into N parts of equal interval

. Thus T = N

, and dt =

0. The transition amplitude <0|X> can be written as :
<0|X> = A

e^{^{(i/)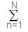L(q_n - q_n-1)}}dq₁

dq_N-1 ---------- (55)
where A is the normalization constant. For a particle in free field L = (m/2)(dq/dt)², A = (m/ih

)^N/2 Eq.(55) can be evaluated analytically :
<0|X> = A

e^{^{(im/2)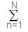(q_n - q_n-1)²}}dq₁

dq_N-1
= (m/ihT)^1/2exp(imX²/2

T) ---------- (56)

Figure 15 Path Integral
[view large image]

The integration is carried out by applying the Gaussian integral :
e^{-f(q_n-q_n-1)²-g(q_n+1-q_n)²}dq_n = [

/(f+g)]^1/2{e^{-[fg/(f+g)](q_n-1-q_n+1)²}} ---------- (57)
repeatedly (N-1) times.

		The real part of the transition amplitude <0\|X> is plotted in Figure 16 and 17 with T and X holding constant respectively. Figure 16 shows that the wavelength is shorter at large X signifying higher probability for particle with higher velocity to get there. On the other hand in Figure 17 for a given X, a particle with lower velocity (and hence longer wavelength) would take longer to reach. But the chance of getting there becomes progressively smaller. Numerical computation is again performed by a home computer with Basic programming. The electron mass m is assumed in the calculation, thus (m/h)^1/2 ~ 0.4 and (m/2) ~ 0.5. For the case of constant T, X is evaluated
Figure 16 X vs Transition Amplitude [view large image]	Figure 17 T vs Transition Amplitude [view large image]	within the range -3 to +3 in step of 0.001 (in unit of cm); while for the case of constant X, T is evaluated from 0.5 to 5 in step of 0.0001 (in unit of sec).

The relative probability P that a particle arrives at point X is :

P = <0|X>*<0|X> = |<0|X>|² = (m/hT) ---------- (58)

These are the formulas originally derived by Feynman in his thesis. The Schrodinger Equation for a free particle can be derived by differentiating the end point (X,T) :
-(

/2m)<0|x> = i<0|x> ---------- (59)
where X, T are replaced by x, t in conformity with convention, and <0|x> is now interpreted as wave function. The particular wave function in the form of <0|x> as shown in Eq.(56) has the initial position as well as the initial time specified. While the commonly quoted wave function

in the form of e^i(kx-t) is not connected to any initial conditions but satisfies the same equation as shown in Eq.(59).

Comparison of the two methods (method 1 for sum over paths and method 2 for sum across paths) is hindered by progressive inaccuracy (in method 1, and in my home computer) as the argument getting larger. However, for the case of free field the action S can be evaluated analytically:

S = (m/2)(X²/T + a²T³/12) ---------- (60)

making the numerical computation less time consuming. The results for the 3 end points in Table 08 are obtained by visual inspection of the asymptotic limits (for method 1, with step for "a" equals to 0.1), and m taking to be the mass of the electron.

X	T	\|<0\|X>₁\|	\|<0\|X>₂\|	\|<0\|X>₂\|/\|<0\|X>₁\|	\|<0\|X>₂\|/T \|<0\|X>₁\|
1	1.0	8.75	0.40	0.045	0.045
1	1.25	6.28	0.36	0.057	0.046
1	1.5	4.80	0.33	0.067	0.045

Table 08 Comparison of Method 1 and 2

There is a third method to evaluate the path integral. It is the variant of method 1 with a twist (literally). Followings are the steps on how it is done:

Replace the summation over all paths with integration of the parameter "a" from -

to +

. Thus, the transition amplitude can be rewritten as:
<0|X>₃ = e^iS/da ---------- (61)

Transform the end time T to -iT' in Eq.(60) for the action S. This is sometimes referred as Wick rotation, which rotates the time axis by 90^o from the Minkowskian spacetime to the Euclidean spacetime. The technique alters the oscillating exponential to a decaying exponential making the integration much easier to carry out. Actually, Method 2 has performed the Wick rotations already implicitly.

Use the Gaussian integral: C e^-kx²+fx+gdx = C(/k)^1/2e^(f²/4k)+g ---------- (62)
to perform the integration.
Reverse the end time transformation from T' to iT after the integration.
The resulting transition amplitude is now in closed form:

<0|X>₃ = (1/iT)(12h/imT)^1/2exp(imX²/2T) (8.94/iT^3/2)exp(imX²/2T) ---------- (63)

By defining <0|X>'₃ = T<0|X>₃, a wave equation can be derived from method 3:
-(

/2m)<0|x>'₃ = i<0|x>'₃ ---------- (64)
with the ratio |<0|X>₂|/|<0|X>'₃| = (m/2h)/3^1/2

0.045 ---------- (65)
The extra factor of "T" is introduced by assuming a set of parabolic curves for the paths as shown in Eq.(52a).

---------------------------------------------------------------------------------------------------------------------------
Finally, there is a website for anyone who aspires to a career in theoretical physics. The website provides links to teach people on the intricacy of particle theories. It was created by Gerard 't Hooft, who showed in 1971 that the gauge bosons in Standard Model could be made massive while preserving renormalizability. He is the recipient of the 1999 Nobel Prize.