Quantum Field Theory

Quantum Vacuum (without Vacuum Catastrophe, 2019)

(Zero Point Energy, Quantum Fields and Vacuum Energy Density,
Hole Theory, Pair Creation and Annihilation)

Zero Point Energy

In classical physics, empty space is called the vacuum. The classical vacuum is utterly featureless. However, in quantum theory, the vacuum is a much more complex entity. The uncertainty principle t E > allows virtual particles (each kind corresponding to a specific quantum field) continually materialize out of the vacuum for a short time and then vanish according to the uncertainty principle (Figure 05p).

Figure 05p Virtual Particle

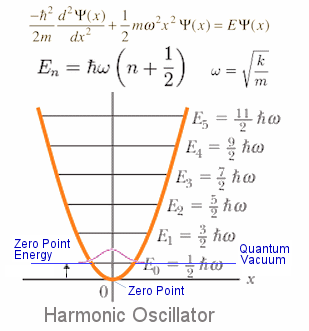Such movement means that there is a lowest energy level for the virtual particles. The lowest part of the quantum fields at vacuum state can be approximated by a harmonic oscillator at each spatial point as shown in Figure 05q. The lowest energy level has an energy E0 = /2 for n = 0 corresponding to no real particle according to "Quantum Field Theory" (QFT). Since there are an infinite number of harmonic oscillators per unit volume, the total zero-point energy density is, in fact, infinite. The process of renormalization is to move the zero point energy up to E0 so that En = n with n = 0, 1, 2, ... ; the infinity is thus removed. Such manipulation is justified by the fact that only the difference in energy is measurable. Now, the quantum vacuum is defined as no excitation of field quanta, i.e., no real particles are present. In other word, it is at a state of minimum (and zero) energy. The classical analogy would be a collection of motionless harmonic oscillators.

Figure 05q Zero Point Energy [view large image]

Quantum Fields and Vacuum Energy Density

It is proposed that there are 24 quantum fields (12 each for fermions and bosons as prescribed by the Standard Model) co-existing in this layer of "zero point energy" (see Figure 05r and further detail in "deeper level"). Here's an attempt to estimate the vacuum energy density with some properties of the quantum fields.


• The anti-symmetric nature of 2 fermions dictates a minimum spatial size in which only one fermion is admissible such that a b. The ultimate minimum has to be a cube with the Planck length L_pl = 1.62x10^-33 cm on each side.



It can be shown that the dynamics of harmonic oscillator can be expressed in terms of the creation and annihilation operators a and a, i.e., the Hamiltonian can be expressed as H = h (aa + 1/2) without referring to the mass (see "Harmonic Oscillators and Quantization of Field"). This form is more suitable in the present context as the quantum fields are supposed to be massless, its corresponding particle acquires mass only when excited and interacting with the Higgs field. Indeed, all the particles gained their respective mass only after the Electro-weak Era some 10-11 sec after the Big Bang (see "Higgs Field Interaction").

Figure 05r Quantum Fields [view large image]

As shown in the Hamiltonian above, the zero point energy for each fermion of the type "k" is Ek = (1/2)hk. Thus, the vacuum energy density is k = Ek / (Lpl)3, where different type of fermion would have its specific frequency k.



• On top of this zero point energy density, there is the contribution of the virtual particles popping up briefly from the zero point (vacuum) state incessantly. To simplify the calculation of the energy density of such activity, the dynamics of the harmonic oscillator is replaced by standing waves in a cube with length L (see the similarity in Figure 05s, and also the Square Well Potential). The simplified derivation in the following shows the huge difference between observation and such explanation.

  Figure 05s Normal Modes [view large image]	This is the so-called "Vacuum Catastrophe". The problem can be solved by noting that contribution from the higher mode is smaller by shorter time fluctuation of the amount t ~ / E according to the uncertainty principle.

  
  
  
• Thus, the so-called Vacuum Catastrophe is resolved. The energy density of zero point and vacuum fluctuation together can now be equated to the observed value of 10^-29 x c² ~ 10^-8 ergs/cm³ or each zero point quanta contains an energy of E_k ~ 10^-107 ergs in an order of magnitude estimation. This vacuum energy density is supposed to be applicable everywhere and at anytime. It is not subjected to the effect of cosmic expansion.


[2024 Update] :

The consideration above is over simplified. According to ChatGPT (in Italic text) :

The idea that higher-energy contributions to the vacuum energy might diminish due to shorter periods (or wavelengths) under the uncertainty principle has been considered within quantum field theory. This concept relates to the regularization and renormalization of vacuum energy, where contributions from high-energy modes are systematically controlled.

Here's how it connects:
Key Considerations:
1. Heisenberg Uncertainty Principle: The principle implies that higher-energy fluctuations correspond to shorter timescales (or shorter wavelengths in spatial terms). The question is whether these fluctuations could "average out" or diminish their net contribution to the vacuum energy.
2. Momentum Cutoff: One way to address the issue is to introduce a cutoff in momentum (or energy), effectively ignoring contributions beyond a certain scale. This is often tied to the Planck scale, where quantum gravity effects are expected to become significant. Such cutoffs reduce the contribution of short-wavelength (high-energy) modes but do not solve the discrepancy without fine-tuning.
3. Dimensional Regularization: Another approach is to mathematically sum these contributions using techniques that inherently cancel divergences. For example, renormalization schemes aim to deal with infinities in quantum field theory, but they still leave the theoretical vacuum energy vastly larger than observed.
4. Physical Interpretations:
o If spacetime itself has a structure (e.g., granularity at the Planck scale), it might naturally suppress high-energy modes' contributions to the vacuum energy.
o Alternatively, in some proposed quantum gravity frameworks, such as string theory or loop quantum gravity, the vacuum energy might emerge in a way that inherently avoids contributions from very short scales.

Challenges: " Magnitude Problem: Even with a cutoff at the Planck scale, the calculated vacuum energy is still about 120 orders of magnitude larger than the observed value of dark energy. " Observational Consistency: The small observed dark energy density remains unexplained in models relying solely on truncating or averaging quantum fluctuations.

Current Outlook: This approach has been useful in understanding aspects of quantum field theory and cosmology but does not fully resolve the cosmological constant problem. The mystery persists, suggesting that we may need new physics-possibly from quantum gravity, holography, or unknown symmetries of spacetime-to explain the smallness of dark energy.


Recent References :

Solution to the cosmological constant problem
The ‘least crazy’ idea: Early dark energy could solve a cosmological conundrum
Is Dark Energy Truly a Constant?

[End of 2024 Update]



To demonstrate the existence of virtual particles, it is noticed that virtual photons in between two parallel metal plates placed a short distance apart can exist only when they can form a standing wave, thus there are fewer photons in each cubic centimeter of vacuum between the plates than there are in the vacuum outside. So, in effect, there is an excess pressure from outside pushing the plates together. This is known as Casimir effect (see Figure 05t). The resulting force is very small, but it has been measured (for plates separated by gaps of a few nanometers), proving that quantum fluctuations of the vacuum are a real phenomenon.

Figure 05t Casimir Effect [view large image]

It is estimated that for a gap d ~ 10-5 cm, the energy in between E ~ c/d ~ 10-12 ergs. The number of zero point quanta N ~ (10-5 x 1)/(Lpl)3 ~ 1094 for 1 cm2 plates. Then the energy contains in one quanta E ~ 10-106 ergs - a rather surprising agreement in magnitude by such crude estimate with the theoretical estimate above.

The dominance of dark energy over matter occurred at about 7 billion years since the Big Bang according to some astronomical observations. It is found that only constant dark energy density or a very slowly varying one in standard cosmology can reproduce a rough match for this value of transitional time. All other forms proportional to 1/Rk (R is the scale factor) would fail the test (Figure 05u). The range of k that can produce a viable cross-over time is shown in the table below :

Figure 05u Dark Energy Era [view large image]

We are going to use the standard cosmological equation with the additional 1/Rk dependence on the cosmological "constant" term (time in unit of 1/H0), i.e.,

(dR/dt)2/R2 = m/R3 + /Rk, which can be recast to express the cosmic acceleration explicitly (d2R/dt2) = R[- m/(2R3) + (1-k/2)/Rk] = 0 at cross-over time; then the scale factor R = eq/(3-k), where q = ln(m) - ln[(2-k)], with m = 0.26, = 0.74; giving the red shift z = (1-R)/R, while the cross-over time since Big Bang in Gyr (109 years) T is computed by a Cosmic Calculator with the above parameters and 1/H0 = 13.7 Gyr (or H0 = 71.4 km/s-Mpc).

cycle. For example, in the current cycle where we happen to live in, the energy density of the false vacuum is about 10119 ergs/cm3. Such energy has been converted to various entities since then. The true vacuum has attained its current value of about 10-8 ergs/cm3 since the beginning of this cycle. Therefore, the calculated vacuum energy density of 10127 ergs/cm3 is not the dark energy, it is instead the energy released into this cycle of the universe (Figure 05v,b). This kind of consideration can be applied to

Figure 05v Dark Energy in Cyclic Universe [view large image]

other cosmological theory in general (such as the inflation theory) with the false vacuum energy density coming from some source.

Hole Theory

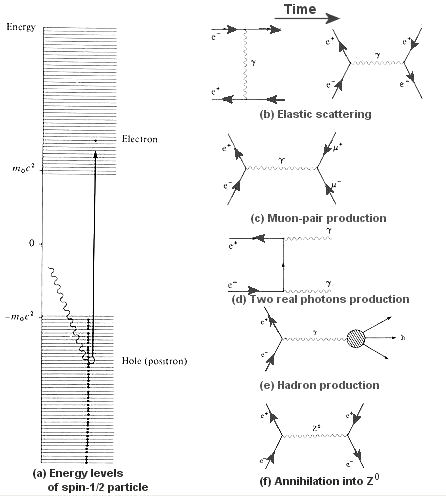Another kind of vacuum structure is prescribed by the Dirac theory of spin-1/2 particles in 1930. It admits the existence of both positive- and negative-energy particles: E = (m02c4 + p2c2)1/2. The concept of negative-energy entities is wholly alien to our knowledge of the universe. All things of physical significance are associated with varying amounts of positive energy. To get around the problem, Dirac proposed an energy spectrum containing all electrons in the universe (see Figure 06a). In addition to the normal positive-energy spectrum, it also contains the negative-energy variety, which spans the spectrum from -m0c2 down to negative infinity. All the negative-energy levels are filled, thus the positive-energy particle is inhibited from transition into these lower energy states. Thus, there is no observable effect in the real world. Only when there is enough energy available, e.g., E 2m0c2, a real particle and anti-particle pair with positive-energy can be created from this unseen sea of negative-energy particles. The particle is

Figure 06a Negative Energy [view large image]

the electron originally resided in the negative energy region, while the anti-particle (positron) can be interpreted as the hole in the vacated energy level acquiring a mass m0. The law of charge conservation demands that this anti-particle carries a positive charge.

Pair Creation and Annihilation

Many interesting things occur when the electron meets the hole (see Figure 06a). Over the past three decades, the use of e⁺e^- collisions to probe the vacuum have yielded a great deal of information about the nature of the strong, weak, and electromagnetic interactions, and have played a major role in establishing the Standard Model of elementary particles. There are many special features of the e⁺e^- experiments:


• The e⁺e^- pair often annihilate into a vacuum state of pure energy (in the form of electromagnetic radiation or other kind of bosons). All the quantum numbers of the initial particles disappear by cancellation. The energy is then free to sample the hidden, negative-energy content of the vacuum without the inhibiting effects of conservation laws. Such energy can be in the form of photon in diagram (a) of Figure 06a boosting any particle pair from the negative-energy sea.
• When an electron and positron are collided head-on, with equal and opposite momentum, the center of mass of the reaction is absolutely stationary. In such circumstance, the angular distribution of created particles can be measured directly and significant asymmetries detected much more easily.
• Since the e⁺e^- pair can annihilate to a vacuum state, it means that the reactions are very clean. There is no debris surviving from the initial state to mask interesting new effects or to confuse the detection.
• The range of phenomena open to study depends upon the total energy of the collision. But while the e⁺e^- beams are kept in orbit they emit their energy in the form of synchrotron radiation. So, to achieve very high energies, it is necessary to build very large rings and to input a lot of radio frequency power to replenish the lost energy. Therefore, the search for new particles has led to the construction of increasingly more powerful and bigger accelerators.

The basic e⁺e^- reactions:


• Electromagnetic processes -
  • The elastic scattering as shown in diagram (b), Figure 06a.
  • Creation of ^+- as shown in diagram (c), Figure 06a. The single photon must be virtual (off-shell) as it does not obey energy-momentum conservation.
  • Production of two real photons as shown in diagram (d), Figure 06a.
  Accurate measurement of these electromagnetic effects is used to test the validity of QED at very high energies. It confirms that the leptons are indeed fundamental point-like particles with size < 10^-16 cm.
• Annihilation into Z⁰ boson - The e⁺e^- can annihilate into Z⁰ boson involving weak interaction (diagram (f), Figure 06a). The virtual Z⁰ boson is free to explore the "weak" content of the vacuum. The electroweak theory predicts that slightly more ⁺s should emerge in one hemisphere than in the other (with the reverse asymmetry for the ^-s). Such parity violation was duly confirmed in 1981.
• Hadron (composite particles containing quarks) productions - One of the most significant quantities in particle physics is the ratio R of the cross section for e⁺e^- hadrons to that for e⁺e^{- +-}, as a function of the colliding energy:

  ---------- (45)

  It compares a well-understood reaction (muon-pair production) with the class of less well-known reactions (hadron production). The ratio R is relatively straight-forward to observe experimentally. Only two charged "prongs" are seen to emerge in muon-pair production whereas, almost invariably, more emerge from a hadronic final state (digram (e), Figure 06a). So the ratio can be obtained from the numbers of these different events. Surprisingly, the ratio R is constant over large energy ranges, indicating that the complicated hadronic state is produced in much the same way as the simple muon pair. In this case, the virtual photon is probing the negative-energy sea of hadrons in the vacuum instead of electrons or muons.

Closer examination of diagram (e), Figure 06a reveals that the intermediate product is a pair of quarks as shown in the insert within Figure 06b. The quark confinement process creates the observed hadrons in the final state. As the quarks are observed to be point-like (in deep inelastic scattering) and spin 1/2, the intermediate process e+e- q is very similar to the process e+e- +-, the only difference being that the charges on the quarks are only some fractions of that on the muons. This explains the constancy of the ratio R mentioned earlier and displayed in Figure 06b. As for the pronounced spikes

Figure 06b Reaction Ratio [view large image]

which punctuate the curve in Figure 06b. These shapes are formed at certain energies of the e+e- collision, when the q pair have just the correct mass to appear as a single-meson resonance. They are the SU(3) flavour symmetry mesons with mass ~ 1 Gev.

the c mesons form a spectrum from the different values for the spin and the orbital angular momentum of the constituent quarks as shown in Figure 06c. In the same notation for the atomic spectra, S, P and D in the diagram refer respectively to orbital angular momentum 0, , and 2. The resemblance to the atomic spectrum is understandable because of asymptotic freedom as the c and bound themselves together loosely. The force between the quarks can be formulated as a potential acting in the vicinity of a colour charge. Thus instead of the Coulomb potential in the case of the atom, the quarks interact via the potential:

Figure 06c [view large image] Meson Spectrum

two-jet event. The fragmentation into hadrons then takes place, preferentially along the direction of the motion the quark and antiquark, resulting in jets of hadrons which become more and more collimated as energy is increased (see left diagram of Figure 06d). The measurement of the angular distribution of jet axes confirms that the spin of quarks is indeed 1/2. At even higher energy the quark or antiquark radiating a gluon, which forms a separate jet of its own.

Figure 06d Two- and Three-Jet Event [view large image]

This three-jet event is shown in the right diagram of Fgiure 06d.

with a much smaller cross section ~ 10-7 b as shown in Figure 06e, in which, diagram (a) shows the photon-photon scattering when E < 2mc2. The process that produces the pair out of the vacuum requires very high photon intensity (such as very powerful laser not yet invented) to compensate for the much lower cross section. The diagram on the right shows the various laser facilities over the years. It predicts the laser capability could reach such requirement (the "Schwinger limit") by 2030.

Figure 06e Schwinger Limit [view large image]

See "What's inside nothing? This laser will rip it up to find out", New Scientist, January 26-February 1, 2019 for the world's most intense laser at ELI (Extreme Light Infra-structure) in Romania, 2019.

Go to Next Section
 or to Top of Page to Select
 or to Main Menu