Superstring Theory

M-theory

The problem with determining a correct Calabi-Yau space is related to the perturbative method used to perform the calculation. In this approximation scheme, each possible Calabi-Yau shape appears to be on equal footing with every other; none is fundamentally singled out by the equations. It is simply not possible to select one Calabi-Yau space from the many others. One of the new approaches to non-perturbative string theory involves M-theory and duality, which in fact force us to reconsider the central role played by strings in supersymmetry. In particular, duality allows us to show that the five previously mentioned superstring theories are nothing but different solutions of a single theory, called "M-theory". In this revised picture, the various string theories are different vacua of the M-theory. While perturbation theory only probes the vicinity of each vacua, duality allows us to make non-perturbative correlations across different vacua. Furthermore, M-theory indicates that the "true home" of the theory may actually be the eleventh dimension, where we find new, exotic objects, such as super membranes and 5-branes. The complete "action" of M-theory is unknown, but is believed to contain membranes (2-branes) and 5-branes. Closed strings in lower dimensions can be viewed as compactifications of these membranes.

T Duality - For the type II string with left- and right-movers in a ten-dimensional spacetime, the T-duality comes about from the curled-up dimension (for example, the 9th dimension). The momentum for the movers are given by the expression similar to Eqs.(45) and (46). It can be shown that with the interchange of (R , 1/2R) and (n , m) the chirality for the left-mover of the 9th dimension spinor flips under this transformation. Since Type IIA string starts out with opposite chirality for the movers, now both movers would have the same chirality, i.e., it changes to a Type IIB string. In other word, by exchanging the radius R and 1/2R (and n, m), one kind of Type II string would change to the other. A more complicated argument shows that similar kind of interchange exists between the SO(32) and E₈ X E₈ superstrings. Since this duality does not involve the coupling constant, which has severe impact on the series expansion, it is applicable even in perturbation theory.

S Duality - S-duality can be examined most easily in Type II string theory, because this theory happens to be S-dual to itself. The low energy limit of Type IIB theory is a supergravity field theory, which features a massless scalar field called dilaton. It can be shown that the Type IIB theory is invariant under a global transformation by the group SL(2,R) with the dilaton field transforming as 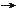- . Since the gravitational coupling constant G = e, the Type IIB theory thus appears to be unchanged when the strong and weak couplings are interchanged. Again, a more complicated argument shows that similar kind of interchange exists between the SO(32) and Type I superstrings.

U Duality and 11 Dimensions - U-duality is essentially a combination of S-duality and T-duality, e.g., U-duality implies that a theory A which is compactified to small size with weak coupling constant is dual to a theory B which is compactified to large size with strong coupling constant. The T-duality and the S-duality groups together only form a subgroup of this larger U-duality group. For example, if we start in either the Heterotic-E or Type IIA regions (see Figure 08) and turn the value of the respective string coupling constants up, what appeard to be one-dimensional

strings stretch into two-dimensional membranes. In the IIA case the eleventh dimension is a tube, whereas in the HE case it is a cylinder (see Figure 09). Moreover, through a more or less intricate sequence of duality relations involving both the string coupling constants and the detailed form of the curled-up spatial dimensions, we can smoothly and continuously move from one string theory to any other. Thus, all the five string theories involve two-dimensional membranes, which become apparent in the strong coupling limit and show up in the 11th dimension.

Figure 09 U Duality
[view large image]

11D-Supergravity - Although the form of the new theory (M-theory) is not known, it should be approximated by the 11-dimensional supergravity for particle at low energies (low compared to the Planck energy). Supergravity attempts to merge general relativity with quantum field theory via the addition of super-symmetry. The 4-dimensional version ultimately met with failure. The formulation in ten or eleven dimensions turned out to be more promising. In fact, there are four different ten-dimensional supergravity theories that differ in details regarding the precise way in which supersymmetry is incorporated. Three of these become the low-energy point-particle approximations to the Type IIA, IIB, and Heterotic-E string. The fourth is the similar limit to the Type I, and Heterotic-O string. The eleven-dimensional supergravity seems to have been left out in the cold until the M-theory comes along.

p-Branes - M-theory reveals that there are higher dimensional objects in string theory with dimensions from zero (a point) to nine, called p-branes. In terms of branes, what we usually call a membrane would be a two-brane, a string is called a one-brane and a point is called a zero-brane. A p-brane is a spacetime object that is a solution to the Einstein equation in the low energy limit of superstring theory, with energy density of the non-gravitational fields confined to

some p-dimensional subspace of the nine space dimensions in the theory. For example, in a solution with electric charge, if the enrgy density in the electromagnetic field was distributed along a line in spacetime, this one-dimensional line would be considered a p-brane with p=1. Figure 10 shows our 3-brane world (blue line) embedded in a p-brane (green plane, p = d₁₁ + 3), along which the light described by open strings propagates, as well as some transverse dimensions (yellow space), where only gravity described by closed strings can propagate. In most respects p-branes appear to be on an equal

Figure 10 p-brane
[view large image]

footing with strings. It has been shown that a p-brane wrapped around a curled-up region of space acts like a particle; thus drastically increases the number of ways the new vacua can be constructed. A p-brane expanding infinitely far in some spatial directions can act

as black hole in the remaining dimensions, trapping objects that come too close. In this view, it is not necessary to compactify the extra dimensions anymore.

D-branes - A D-brane is a submanifold of space-time with the property that open strings can end or begin on it. Strings can have various kinds of boundary conditions. For example closed strings have periodic boundary conditions (the string comes back onto itself). Open strings can have two different kinds of boundary conditions called Neumann and Dirichlet boundary conditions. With Neumann boundary conditions the endpoint is free to move about but no momentum flows out. With Dirichlet boundary conditions the endpoint is fixed to move only on some manifold. This manifold is called a D-brane or Dp-brane ('p' is an integer which is the number of spatial dimensions of the manifold). For example we see open strings with one or both endpoints fixed on a 2-dimensional D-brane or D2-brane (see Figure 11a). The D9-brane is the upper limit in superstring theory. Notice that in this case the endpoints are fixed on a manifold that fills all of space so it is really free to move anywhere and this is just a Neumann boundary condition. The case p= -1 is when all the space and time coordinates are fixed, this is called an instanton or D-instanton. When p=0 all the spatial coordinates are fixed so the endpoint must live at a single point in space, therefore the D0-brane is also called a D-particle. Likewise the D1-brane is also called a D-string. D-branes are actually dynamical objects which have fluctuations and can move around. For example they interact with gravity. In Figure 11b we see

		one way in which a closed string (graviton) can interact with a D2-brane. Notice how the closed string becomes an open string with endpoints on the D-brane at the intermediate point in the interaction. Compacti-fication of the 11 dimension will generally produce even dimensional D-branes for the Type IIA string, and odd
Figure 11a D-brane [view large image]	Figure 11b D-brane Inter- action [view large image]	dimensional D-branes for the Type IIB string (see Figure 08). M-theory contains only 5-branes, membranes, and gravitons.

The interesting property of D-brane is that the segments of string on the brane behave just like elementary particles. The only thing missing on the D-brane is gravity. That's because the graviton is a closed string - a string with no ends would not be stuck to the brane at all. Instead, they can travel freely through all space. They can interact with other strings by moving in and out of the brane. According to string theorists we are most likely living in a D3-brane with six dimensions tightly rolled up. Such configuration would prevent gravity from spreading out too much.

It has been shown that D-branes and p-branes are actually the same thing. Branes are not merely places; they are also objects that possess finite tension and carry charges. Thus, they can be distorted and can interact with other charged objects and gravitational field. They can move, collide, annihilate, and even form systems of branes orbiting around one another. On the other hand, brane can provide an environment for the strings to play their roles. Since the gauge bosons are also open strings, they would communicate a force that would act on the other brane-bound open strings with charge (at the endpoint). The photon being one of the gauge bosons is also trapped within the D3 brane; thus guarantees that the principle of special relativity (about the constant speed of light in our three dimensional space) is not violated. In short, the D3 brane would contain all the particles and forces in the Standard Model. From the perspective of brane-bound particles, if it weren't for gravity or other bulk particles with which they might interact, the world might as well have only the dimensions of the branes.

Cosmic String -Recently in 2003, a peculiar object known as CSL-1 was found by an Italian-Russian group. It consists of two apparently identical elliptical galaxies roughly at a distance of 10 billion light years from Earth and a mere 2 arc-seconds apart. The most intriguing property of CSL-1 is that the object is clearly extended and the isophotes of the two sources show no distortion at all. Both images have a redshift of 0.46, and the two spectra are identical at a 99.96% confidence level (see Figure 11c). There is no intervening galaxy or cluster of galaxies to produce the images by gravitational lensing. Follow-up observation reveals 11 other double images in a field 16 arc-minutes square centred on CSL-1. Researchers are wary of rushing to conclusions. More observations is needed to confirm such an explanation.

		There are at least three theories for producing long thin and heavy cosmic string from the early universe. It is used to explain the identical images such as the CSL-1 (Figure 11d). 1. Force fields pointing to different directions were frozen into long string during the phase transitions as the universe cooled down rapidly after the initial inflation. It is similar to the cracking ice and defects formed in liquid helium and superconductor. 2. Superstring theorists have found that by wrapping the extra dimensions in a special way, the tiny superstring could be inflated into the cosmic string. 3. Another explanation involves a D-brane, which intersect with only one dimension of our universe. As a result, it looks like an
Figure 11c CSL-1 [view large image]	Figure 11d Cosmic String Models [view large image]	one dimensional object. The energy within distorts the space around and bends the light from more distance galaxies to produce the double images.

Scientists in 2006 offer another explanation for the paired images of CSL-1 via the reformulated theory of cosmic strings, which emerged from the cosmic inflation in a spaghetti-like tangle. Although thinner than subatomic particles,

cosmic strings are boundless in length, stretched by cosmic expansion across the universe. They are characterized by huge linear density of 1 million metric mega-tons per centimeter. If a cosmic string runs between the Milky Way and another galaxy, light from that galaxy would go around the string symmetrically, producing 2 identical images near each other in the sky as shown by CSL-1. Figure 11e depicts a simulation of the evolution of cosmic strings from the radiation-dominated universe (left) to the matter

Figure 11e Cosmic Strings
[view large image]

dominated era (right), which shows a much lower density of both long strings and loops, and fewer wiggles in the long strings.

It is shown in 2008 by the Hubble space telescope that the two images in CSL-1 were two different, deceptively similar galaxies. Thus like so many exotic objects concocted by theorists, cosmic string remains just a hypothetical entity.