

Figure 13-08u Ohm`s Law in Electricity [view large image]
 =
=  and R = 0 so that the current I can run forever without applying any voltage.
and R = 0 so that the current I can run forever without applying any voltage.| Home Page | Overview | Site Map | Index | Appendix | Illustration | About | Contact | Update | FAQ |
 |

|
Figure 13-08u Ohm`s Law in Electricity [view large image] |
In super-conductive state, the electrons move coherently as a whole; thus  = =  and R = 0 so that the current I can run forever without applying any voltage. and R = 0 so that the current I can run forever without applying any voltage. |
 0 - 1/ohm-cm = 1/sec.
0 - 1/ohm-cm = 1/sec. |

|
Figure 13-08v Hall Effect, Classical |
On the other hand with known electron density, it can be turned into a magnetometer to measure the magnetic field from the reading of VH (Figure 13-08v,b). |
 as (vector is denoted by boldface letter, the dimension of number density n is #/cm2 instead of #/cm3 in the 3-D case) :
as (vector is denoted by boldface letter, the dimension of number density n is #/cm2 instead of #/cm3 in the 3-D case) :
 |

|
Figure 13-08w Landau Distribution [view large image] |
 |
 = eB/m defined above is the cyclotron frequency related to the circular motion of electron confined by the magnetic field B, while
= eB/m defined above is the cyclotron frequency related to the circular motion of electron confined by the magnetic field B, while  = (K/m)1/2 is for the harmonic osciallation where K is the force constant of the spring. Similarly,
= (K/m)1/2 is for the harmonic osciallation where K is the force constant of the spring. Similarly,  = (
= ( /eB)1/2 is the cyclotron radius, now the angular momentum L = m
/eB)1/2 is the cyclotron radius, now the angular momentum L = m
 =
=  instead of mvr in the classical definition. Therefore, the orbital angular momentum in this case is quantized with an integer quantum number 1.
instead of mvr in the classical definition. Therefore, the orbital angular momentum in this case is quantized with an integer quantum number 1.
 |
levels to a broader spectrum of levels as shown in Figure 13-08w. Since the spin and ky do not appear in the Landau levels, it is degenerate as shown in the same image. The different electron orbitals for different Landau levels are displayed at the bottom as well. Experimental measurement gives  xy = 1/25812.807557 ohm-1, which allows precise determination of some physical constants (see "Quantum Hall Effect Applications"). Figure 13-08x1 shows the step-wise increment of the resistivity/conductivity as function xy = 1/25812.807557 ohm-1, which allows precise determination of some physical constants (see "Quantum Hall Effect Applications"). Figure 13-08x1 shows the step-wise increment of the resistivity/conductivity as function |
Figure 13-08x1 QH Conductivity, Experiment |
of the magnetic field B and the number density n (negative number represents hole with +|e| ). The  xx is also present as it is not exactly equal to zero in the real world. The quantum steps can be interpreted as a topological phenomenon, for which changes to the system's properties could not occur smoothly. xx is also present as it is not exactly equal to zero in the real world. The quantum steps can be interpreted as a topological phenomenon, for which changes to the system's properties could not occur smoothly. |
 |
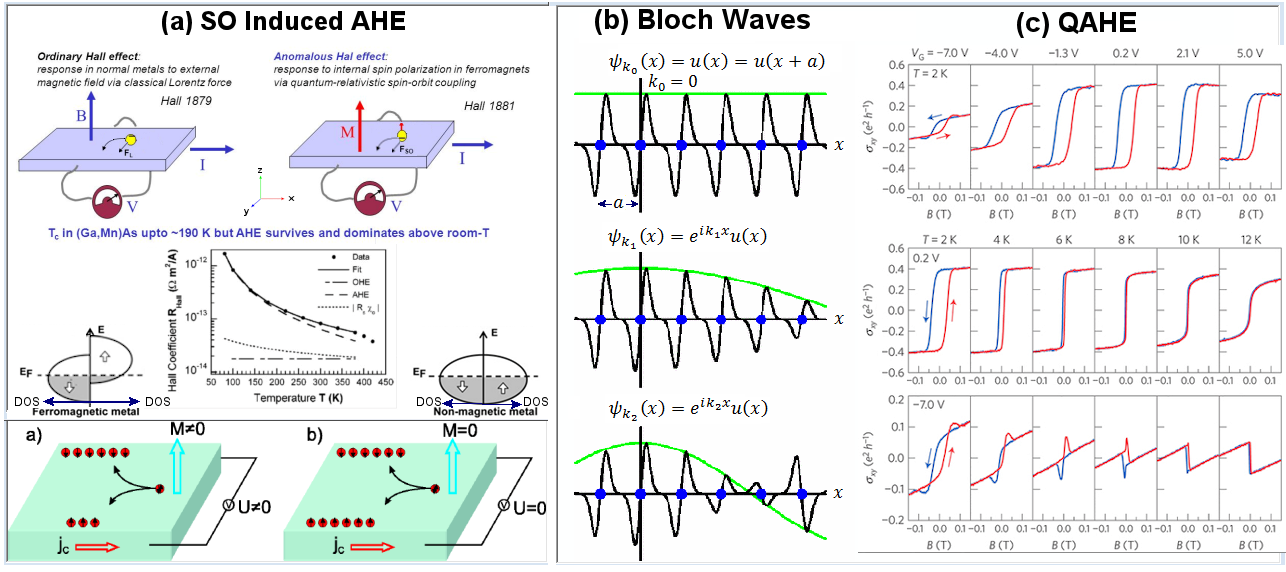
The Chern class in topology is used to classify geometric objects into different categories. As shown in Figure 12-08x2,b, it is defined as the surface integral in a patch of the object. The concept is now applied to the low temperature physics, in which it is discovered that the magnetic property in k-space can be identified to the topological formula (with the Chern number  replaced by C, see Figure 13-08x2,a). Thus, in the bulk of the topological material C = 0, while it is C = 1, 2, 3, ... in different energy levels at the edge; the values of the conductivity/resistivity would vary in steep steps corresponding to the change in Chern number (in discrete steps). Ultimately, it is the variation of the wave function (from whatever cause in k-space) that induces the phenomena in the various replaced by C, see Figure 13-08x2,a). Thus, in the bulk of the topological material C = 0, while it is C = 1, 2, 3, ... in different energy levels at the edge; the values of the conductivity/resistivity would vary in steep steps corresponding to the change in Chern number (in discrete steps). Ultimately, it is the variation of the wave function (from whatever cause in k-space) that induces the phenomena in the various
|
Figure 13-08x2 Topological Interpretation |
kinds of Hall effects. The reason behind the appearance of the Chern number becomes apparent if the surface integral is transformed to a line integral (of a closed loop around the surface in k-space) by the Stokes' Theorem :  |
 0 = h/e ~ 4x10-15 joules/amp, the Hall resistivity changes in step of h/e2 ~ 2.5x104 joules/amp-C ~ 4x10-15 joules/amp since there are 6x1018 electrons in 1 C (Coulomb). Both cases have their origin in current loop, the extra "e" power in Hall resistivity comes from a collection of electrons instead of from a single one.
0 = h/e ~ 4x10-15 joules/amp, the Hall resistivity changes in step of h/e2 ~ 2.5x104 joules/amp-C ~ 4x10-15 joules/amp since there are 6x1018 electrons in 1 C (Coulomb). Both cases have their origin in current loop, the extra "e" power in Hall resistivity comes from a collection of electrons instead of from a single one. 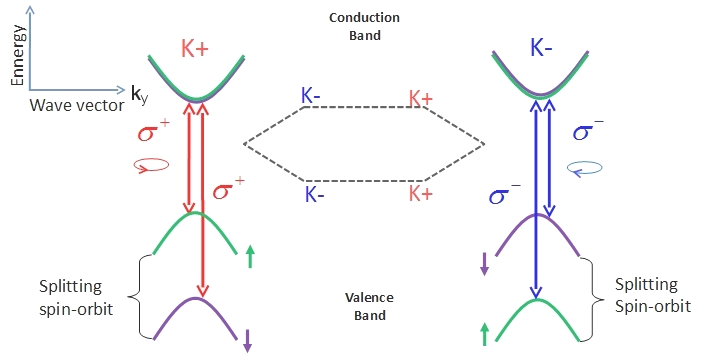 |
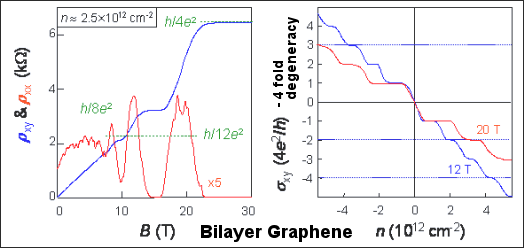
particular values of ky at the valley between the valence and conduction bands making a total of 2x2 = 4 (see Figure 13-08y). In addition, if there is a boundary in the y-direction for example, then the degeneracy for ky is 2( / / 0), where 0), where  is the magnetic flux equals to BxS (S is the surface area) and is the magnetic flux equals to BxS (S is the surface area) and  0 = h/e = 4x10-15 Web is the fundamental quantum flux constant. Thus, the degeneracy normally is a huge number more than 1015, so that all the free electrons in the system sit in only a few Landau levels. It is under such condition where the quantum Hall effect arises. 0 = h/e = 4x10-15 Web is the fundamental quantum flux constant. Thus, the degeneracy normally is a huge number more than 1015, so that all the free electrons in the system sit in only a few Landau levels. It is under such condition where the quantum Hall effect arises.
|
Figure 13-08y Landau Level Degeneracy [view large image] |
See "Spin-Valley Coupling", and "Landau Quantization". |
 |
|
Figure 13-08z1 Hall Effect 2-D Quantum Spin [view large image] |
It can be visualized that the electron charge (current) gives rise to one facet of the Hall Effect, while its spin (current) presents a different view, and thus ushers in the "spintronic" era. |
 |
|
Figure 13-08z2 QSH Effect |
Such QSH effect is observed one year after the theoretical prediction. Cheaper compounds based around bismuth are now available even in 3-D. Its prospects in applications such as quantum computing etc. has opened up a new class of sought-after material, e.g., the topological insulator. |
 |
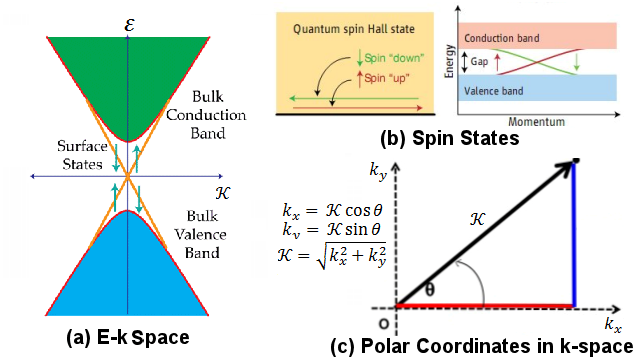
Figure 13-08z3 illustrates the origin of band structure in terms of the dependence of the energy E on the linear momentum  k. The dashed line represents the completely free electron gas within the material. In reality, the electron does interact with the atomic nuclei producing the discrete segment of curves with a gap in between. It is spatially corresponding to the site of the nuclei (see reciprocal separation of distance "n k. The dashed line represents the completely free electron gas within the material. In reality, the electron does interact with the atomic nuclei producing the discrete segment of curves with a gap in between. It is spatially corresponding to the site of the nuclei (see reciprocal separation of distance "n /a" at the k axis). The level of zero energy is often shifted up resulting in negative energy as shown in Figure 13-08z2,b. In addition, the mirror image in k are also displaced in units of 2n( /a" at the k axis). The level of zero energy is often shifted up resulting in negative energy as shown in Figure 13-08z2,b. In addition, the mirror image in k are also displaced in units of 2n( /a) to produce valley and peak instead of disjointed segments. /a) to produce valley and peak instead of disjointed segments.
|
Figure 13-08z3 Band Structure [view large image] |
See the definitions of various bands in Figure 13-08z2,d, and "Topological Insulator" for explicit derivation of 2-D spin-orbit coupling etc. |
 |

|
Figure 13-08z4 QAH Effect |
 |

 = 0 in the bulk to
= 0 in the bulk to  = 1 at the edge in this case).
= 1 at the edge in this case). xy and applied magnetic field B(T). The top one with various gate voltages Vg , and with various temperatures in the next two rows at Vg = 0.2V and -7.0V respectively. The red (blue) arrows and curves represent the process of increasing (decreasing) magnetic field. It illustrates the conductivity increases (decrease) in steep step near B(T) = 0 for all cases. The graphs also shows that the effect dissolves at high gate voltage and high temperature. Actually, most of the Hall effects have to be run at low temperature, because thermal agitation will destroy the rather minuscule interaction. The newly observed effect may have potential applications in future electronic devices.
xy and applied magnetic field B(T). The top one with various gate voltages Vg , and with various temperatures in the next two rows at Vg = 0.2V and -7.0V respectively. The red (blue) arrows and curves represent the process of increasing (decreasing) magnetic field. It illustrates the conductivity increases (decrease) in steep step near B(T) = 0 for all cases. The graphs also shows that the effect dissolves at high gate voltage and high temperature. Actually, most of the Hall effects have to be run at low temperature, because thermal agitation will destroy the rather minuscule interaction. The newly observed effect may have potential applications in future electronic devices.
 |
Normally, the electron is not really free within the crystal lattices, its wave function is in the form of Bloch Wave (see QAHE). However, the spin-orbit coupling could create edge states to link the two separated bands together making them in contact at a point where the electron behaves like a free particle (see Figures 13-08z2 and 13-08z3). The eigen-energy at the bulk is  2k2/2m (denote by k2 henceforth to simply the formulas). It has four-fold degeneracy - 2 from spin up and down ( 2k2/2m (denote by k2 henceforth to simply the formulas). It has four-fold degeneracy - 2 from spin up and down ( (0), (0),  (1)); another 2 from the the directions of the momentum (1)); another 2 from the the directions of the momentum  k. At the edge, by shifting the origin of the E-k space to the contacting point (Figure 13-08z5,a), the k. At the edge, by shifting the origin of the E-k space to the contacting point (Figure 13-08z5,a), the
|
Figure 13-08z5 Topological Insulator, 2D |
effect of spin near this point can be written in term of the spin states and k dependent coefficients (in k-space and matrix notation with the kx i ky terms acting like magnetic field, see 2-D Hall Effect) : i ky terms acting like magnetic field, see 2-D Hall Effect) : |


 |

|
Figure 13-08z6 3D Topological Insulator |
 |
 |
If the topological insulator is placed in close contact with a superconductor, the constituent in the surface state becomes Majorana quasiparticle. It is a bound state of a hole and an electorn resulting in a quasiparticle which is its own anti-quasiparticle and often mis-labeled as Majorana fermion which is a fundamental particle like Majorana neutrino (Figure 13-08z7,a,b). Anyway, this kind of material is known as topological superconductor. In term of the E-k space, it is the product of merging a band in the bulk (the tl) into a band in the superconductor. |
Figure 13-08z7 3D Topological Superconductor |
Different energy states appear as shown in the right side of Figure 13-08z7,c. This novel material is anticipated to have important quantum computing applications via its properties of non-abelian statistics and non-local interaction (entanglement). |
 |
The example of graphene below is a semimetal in which both the bulk and edge has overlap between the conduction and valence bands. Whereas for topological insulator these bands in the bulk are disconnected, only the edge (or surface in the case of 3-D) has overlapping bands and is robust against perturbations. Nevertheless, the methodology is also applicable to discover the characteristics of metals and semimetals as well as topological insulators (see Figure 13-08z8, in which the Fermi Energy EF can be |
Figure 13-08z8 Energy Bands, Types [view large image] |
considered as the highest filled energy level at absolute temperature T = 0. For finite temperature, there could be some diffusion of electrons into energy level higher than EF depending on the type of energy band). |
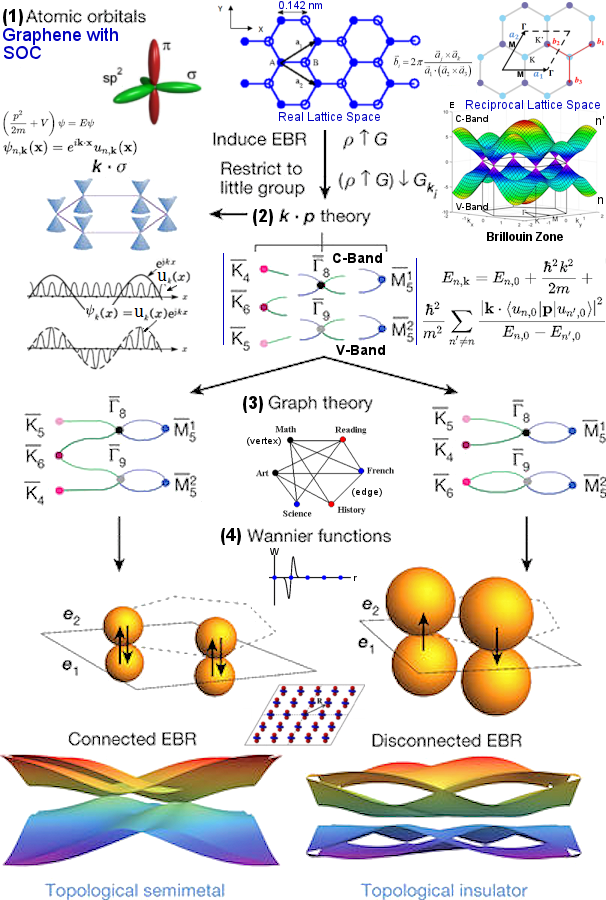 |
 in the middle, K at the corners, and M the middle of the hexagonal side, see Figure 13-08z9,1). in the middle, K at the corners, and M the middle of the hexagonal side, see Figure 13-08z9,1). p Theory - The quantum states of an electron in the periodic potential V is determined by the Schrodinger Equation as shown in Figure 13-08z9,2. The wave function can be separated into a cyclic part eikx and the Bloch Wave un,k(x), where k denotes the reciprocal vector in the k-space, a.k.a., reciprocal / momentum space. By shifting the origin of the k-space to the high-symmetry points (thus, k = 0), the solution is just another periodic function un,0(x) where n refers to each individual band. There is no analytic solution for k p Theory - The quantum states of an electron in the periodic potential V is determined by the Schrodinger Equation as shown in Figure 13-08z9,2. The wave function can be separated into a cyclic part eikx and the Bloch Wave un,k(x), where k denotes the reciprocal vector in the k-space, a.k.a., reciprocal / momentum space. By shifting the origin of the k-space to the high-symmetry points (thus, k = 0), the solution is just another periodic function un,0(x) where n refers to each individual band. There is no analytic solution for k  0, a perturbation method (k 0, a perturbation method (k p theory) can be used to obtain approximation for small k such as the dispersion energy shown in Figure 13-08z9,2. p theory) can be used to obtain approximation for small k such as the dispersion energy shown in Figure 13-08z9,2. |
Figure 13-08z9 Topo-Insu, Two Views United [view large image] |
Topological semimetal or insulator can be deciphered according to whether the Wannier functions of the two energy bands are connected at the site or not as shown in Figure 13-08z9,4. |